Тема 2. Параметри розподілу ознак

Вивчення даної теми допоможе Вам адекватно оперувати поняттями «ознаки», «показники», «змінні», характеризуючи розподіл отриманих у дослідженні даних, користуватися параметрами розподілу (математичним очікуванням, дисперсією, показниками асиметрії та ексцесу) у своєї дослідницькій діяльності.

Важливим моментом при вимірюванні психічних явищ є визначення їхніх ознак. Ознака – це індикатор психологічного явища, що виявляється в поведінці людини. (за П.Д.Павленюк). Тобто, це такий зовнішній прояв, який можна спостерігати або виміряти певним приладом. Наприклад: кількість помилок, зроблених при виконанні методики «Кільця Ландольта», є ознакою зосередженості уваги.

Змінна (там же) - це випадкова величина, оскільки наперед невідомо, яке саме значення вона прийме. Так, у математиці змінна «х» - позначення, що замінює певне число.

В психометрії часто поняття ознаки і змінної можуть використовуватися як взаємозамінні. Іноді замість них використовуються поняття показника або рівня, наприклад, рівень наполегливості, показник вербального інтелекту та ін.

Показник – якісні та кількісні характеристики станів об’єкту (там же).

Рівень – умовна горизонтальна лінія, що служить межею висоти прояву, розвитку, мірою значущості чогось (там же)

Поняття показника і рівня указують на те, що ознака може бути зміряна кількісно, оскільки до них застосовні визначення "високий" або "низький", наприклад, високий рівень інтелекту, низькі показники тривожності й ін.

Математична обробка - це операція із індивідуальними значеннями ознаки, одержаними у випробовуваних в психологічному дослідженні.

Розподілом ознаки називається закономірність зустрічаємості її різних індивідуальних значень (Сидоренко О.В).

У психологічних дослідженнях частіше за все посилаються на нормальний розподіл. Нормальний розподіл характеризується тим, що крайні значення ознаки в ньому зустрічаються достатньо рідко, а значення, близькі до середньої величини - досить часто.

Нормальним такий розподіл став називатися тому, що він найчастіше за інші зустрічався у природничих наукових досліджень і вважався "нормою" для будь-якого масового випадкового прояву ознак.

Цей розподіл відповідає закону, відкритому трьома ученими в різний час: Муавром в 1733 р. в Англії, Гаусом в 1809 р. в Німеччині і Лапласом в 1812 р. у Франції (Гласс Дж, Стэнли Дж. ).

Графік нормального розподілу має вигляд звичної для ока психолога-дослідника так званої дзвіноподібної кривої.

Параметри розподілу - це його числові характеристики, які вказують, де "в середньому" розташовуються значення ознаки, наскільки ці значення мінливі і чи спостерігається переважна поява певних значень ознаки.

Найбільш практично важливими параметрами є характеристики центру розподілу, дисперсія, показники асиметрії і ексцесу.

У реальних психологічних дослідженнях ми оперуємо не параметрами, а їх наближеними значеннями, так званими оцінками параметрів. Це пояснюється обмеженістю обстежених вибірок. Чим більше вибірка, тим ближче може бути оцінка параметра до його істинного значення. Надалі, кажучи про параметри, ми матимемо на увазі їх оцінки.

До характеристик центру розподілу відносять середнє значення, моду та медіану

Середнє арифметичне значення характеризує типовий рівень ознаки в сукупності. Обчислюється за формулою:

,

де x_i - кожне індивідуальне значення ознаки; i - індекс, що вказує на порядковий номер значення ознаки; п - кількість спостережень; ∑- знак підсумовування.

Розглянемо приклад: Маємо результати дослідження (стовпчик «xi»), наведені у таблиці 1.

Таблиця 1.

Визначення параметрів розподілу ознак

№	xi	xi – M	(xi-М)2	(xi-М)3	(xi-М)4
	1	-1,5	2,25	-3,375	5,0625
	2	-0,5	0,25	-0,125	0,0625
	3	0,5	0,25	0,125	0,0625
	4	1,5	2,25	3,375	5,0625
	4	1,5	2,25	3,375	5,0625
	3	0,5	0,25	0,125	0,0625
	1	-1,5	2,25	-3,375	5,0625
	2	-0,5	0,25	-0,125	0,0625
	2	-0,5	0,25	-0,125	0,0625
	3	0,5	0,25	0,125	0,0625
Σ =	25		10,5	0	20,625
М =	2,5
Мо=	2; 3
Me=	2,5
S2 =	1,17
σ =	1,08
A =	0
E =	-1,48

Знаходимо суму всіх значень (25), заносимо у клітинку в рядку «Σ =». Це значення треба поділити на кількість спостережень, тобто, у нашому випадку, на 10.

Отримуємо середнє значення «М», яке дорівнює 2,5. Заносимо у клітинку в рядку «М=». Також можна скористатися функцією «СРЗНАЧ» у пакеті Microsoft Excel, що безсумнівно зручніше.

Отже, ми з’ясували, що центр розподілу знаходиться у точці 2,5 бала, тобто в середньому випробувані набирають приблизно такий бал.

Модою (Мо) називають найпоширеніше значення ознаки. Якщо індивідуальних значень у вибірці небагато, її можна визначити візуально за найбільшою частотою. Якщо Ви маєте справу з великим масивом даних, раджу скористуватися функцією «МОДА» у пакеті Microsoft Excel. Для нашого прикладу це не обов’язково, оскільки шляхом простого підрахунку частот можна визначити, що у розподілі дві моди Мо₁=2; Мо₂=3, а середнє значення 2,5 знаходиться точно між ними.

Медіана (Me) — це таке значення ознаки, яке при­падає на середину впорядкованого ряду, поділяючи його на дві рівні за обсягом частини. Тобто половина чисел мають значення більші, ніж медіана, а половина чисел мають значення менші, ніж медіана. Для того, щоб визначити медіану розподілу, індивідуальні дані слід упорядкувати по їх зростанню, це дозволить з’ясувати, що перші 50% значень охоплюються діапазоном від 1 до 2 балів, а другі 50% - діапазоном від 3 до 4 балів. Тому медіана у нашому випадку дорівнює 2,5 бала, а отже збігається з середнім арифметичним у вибірці. Якщо Ви маєте справу з великим масивом даних, раджу скористуватися функцією «МЕДИАНА» у пакеті Microsoft Excel.

Узагальнимо отримані результати: середнє значення збігається з медіаною розподілу та рівновідстоїть від двох мод, отже загалом наш розподіл за формою є симетричними і наближається до нормального, але відрізняється від нього за певними параметрами (адже він має дві моди).

Для того, щоб охарактеризувати ступінь розкиду окремих значень навколо середньої арифметичної, використовують різні способи залежно від вимірюваної шкали. Зокрема, для шкал інтервалів та відношень застосовують оцінки дисперсії та середнього квадратичного відхилення.

Дисперсія, як показник варіації (мінливості) індивідуальних значень, визначає відхилення індивідуальних значень ознаки від центра розподілу, поданого середньою величиною. Інакше кажучи, значення дисперсії покаже нам, наскільки точно середнє значення здатне характеризувати весь розподіл.

Оцінка дисперсії здійснюється за формулою:

Для приклада знову звернемося до таблиці 1. Для того, щоб розрахувати дисперсію, спочатку слід заповнити стовпчики «x_i–M» (шляхом віднімання середнього значення від кожного індивідуального) і «(x_i-М)²» (піднесення отриманих різниць до квадрату). Суму чисел, отриманих у стовпчику «(x_i-М)²» занесемо у відповідну клітинку в рядку «Σ =». У нашому випадку – це значення дорівнює 10,5. Для того, щоб знайти значення дисперсії, нам треба це число поділити на «n-1», у нашому випадку на 9. Отримуємо значення дисперсії «S²», яке дорівнює 1,17. Заносимо у клітинку в рядку «S²=». Якщо Ви працюєте з пакетом Microsoft Excel, скористайтеся функцією «ДИСП» у пакеті Microsoft Excel.

Величина, що є квадратним коренем з оцінки дисперсії, називається стандартним відхиленням або середнім квадратичним відхиленням, вона показує, наскільки широким є розрив між значеннями конкретного спостереження та середнім значенням. Більшість дослідників зазвичай позначають цю величину грецькою буквою σ (сигма), а не S.

Для того, щоб розрахувати стандартне відхилення в нашому випадку достатньо знайти квадратний корінь з уже обчисленої дисперсії, тобто σ =√1,17=1,08. Заносимо це значення у клітинку в рядку «σ =».

Про що свідчить таке значення? Враховуючи той факт, що всі індивідуальні значення у нашому прикладі знаходяться у діапазоні від 1 до 4 балів, а середнє значення дорівнює 2,5 бала, то стандартне відхилення 1,08 – досить велике, а отже середня оцінка не досить точно відображає наш розподіл.

Для того, щоб точніше оцінити ступень однорідності сукупності, використовують квадратичний коефіцієнт варіації V_: , значення якого в симетричному розподілі становить V_ =33.

Характеризуючи далі наш розподіл зазначимо таку закономірність: якщо він симетричний, всі три характеристи­ки центра розподілу однакові: М_о=М_е=М. У помірно асимет­ричному - відстань медіани до середньої втричі менша за від­стань середньої до моди, тобто 3(М - M_e)  М-M_o.

Асиметричний розподіл утворюється у тих випадках, коли певні причини сприяють більш частій появі значень, які вище або, навпаки, нижче за середнє арифметичне значення.

При лівобічній, або позитивній, асиметрії в розподілі частіше зустрічаються більш низькі значення ознаки, а при правобічна, або негативна - більш високі (див. рис.1).

Показник асиметрії (А) обчислюється по формулі:

Для симетричних розподілів А=0.

Ми вже знаємо, що у нашому прикладі розподіл симетричний. Підтвердимо це розрахунками, для чого заповнимо стовпчик «(x_i-М)». Суму чисел, отриманих у стовпчику «(x_i-М)³» занесемо у відповідну клітинку в рядку «Σ =».

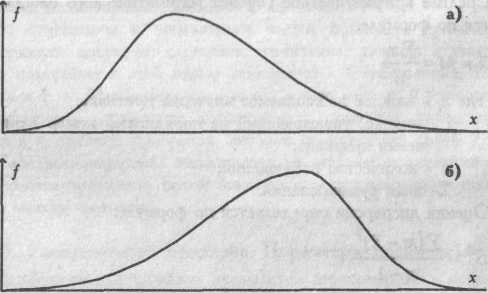
Рис.1. Асиметрія розподілів

а) ліва, позитивна;

б) права, негативна

У нашому випадку – це значення дорівнює 0. Заносимо значення у клітинку в рядку «А=». Також можна скористатися функцією «СКОС» у пакеті Microsoft Excel.

Ексцес характеризує відносну гостроту або згладженість розподілу в порівнянні з нормальним. У тих випадках, коли які-небудь причини сприяють переважній появі середніх або близьких до середніх значень, утворюється розподіл з позитивним ексцесом. Якщо ж в розподілі переважають крайні значення, причому одночасно і більш низькі, і більш високі, то такий розподіл характеризується негативним ексцесом і в центрі розподілу може утворитися западина, що перетворює його на двовершинний (див. Рис. 2).

Показник ексцесу (Е) визначається по формулі:

Рис. 2. Ексцес. а) позитивний; б) негативний.

Можна також скористатися функцією «ЭКСЦЕСС» у пакеті Microsoft Excel.

Якщо звернутися до нашого прикладу, ми можемо, вже виходячи з попередніх даних припустити, що ексцес матиме від’ємне значення, тобто буде негативним. Перевіримо наше припущення. Для розрахунку ексцесу заповнимо останній стовпчик нашої таблиці 1, далі виконаємо розрахунок за формулою.

Отже, ми маємо негативний ексцес, що свідчить про відхилення форми розподілу від нормального через його двовершинність.

Закінчуючи пояснення щодо визначення характеру розподілу вибіркових даних, зверніть увагу на таке:

Запам’ятайте! Параметри розподілу можна визначити тільки по відношенню до даних, представлених принаймні в інтервальній шкалі.

Питання для самоконтролю:

1. У яких випадках слід використовувати поняття «ознака», «змінна», «показник», «рівень», а в яких цього робити не можна?

2. Як називається Гаусовський розподіл, чим він характеризується?

3. Які параметри розподілу Вам відомі?

4. Що означає у формулах різних параметрів розподілу змінна «х_і», позначка «∑»?

Тестові завдання:

1. Вставте пропущене слово: Графік нормального розподілу має вигляд __________________ кривої.

2. Вставте у реченнях замість пропусків слова «ознака», «змінна», «показник» або «рівень»:

а) У студента виявлений високий _________ знань з дисципліни.

б) Зазвичай у формулах ___________ «n» позначає кількість спостережень.

в) Методика дозволяє охарактеризувати емпатію за кількома _____________ .

г) Похмуре обличчя є _______________ поганого настрою.

Завдання для самостійної роботи:

1. Користуючись індивідуальними результатами, отриманими за методикою «Діагностика емоційної зрілості» О.Я.Чебикіна (додаток А) визначте параметри розподілу показника ЕЗ. При цьому, рекомендуємо скористатися наведеною нижче таблицею 2.

Таблиця 2.

№	xi	xi – M	(xi-М)2	(xi-М)3	(xi-М)4
Σ =
М =
S2 =
σ =
A =
E =

2. Подайте характеристику розподілу цих даних, відповівши на наступні питання:

2.1. Де знаходиться центр розподілу?

2.2. Наскільки варіативними є індивідуальні дані відносно цього центру?

2.3. Чи відрізняється розподіл даних від нормального? Який його вигляд?

Література

1. Практикум по общей, экспериментальной и прикладной психологии: Учеб. пособие /Под ред. АА.Крылова, С.А. Маничева. – СПБ.: Питер, 2000. – 560 с.

2. Бурлачук Л.Ф.,Морозов С.М. Словарь- справочник по психологической диагностике - Киев: Наук. думка, 1989

3. Сидоренко Е.В. Методы математической обработки в психологии – СПб.: ООО «Речь», 2004. – 350 с

4. Гласс Дж, Стэнли Дж. Статистические методы в педагогике и психологии. - М.,1976.

5. Краткий словарь по социологии /сост. П.Д.Павленюк. – М., 2004. – 272 с.