§7 Рух заряджених часток у магнітному полі

Сила Лоренца завжди перпендикулярна швидкості руху зарядженої частки, тому вона змінює тільки напрямок швидкості, не змінюючи її величини. Отже, сила Лоренца роботи не виконує

 (т.к.  )

т.т. постійне магнітне поле не робить роботи над зарядженою часткою, що рухається в ньому, і кінетична енергія цієї частки в магнітному полі не змінюється.

1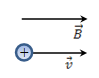 . Якщо частка влітає в магнітне поле й при цьому вектор швидкості   паралельний вектору  , тто sinα = 0, F_Л = 0, і частка рухається за інерцією прямолінійно рівномірно.

F_Л = 0;                  S=vt.

 

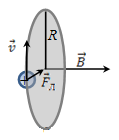
2. Якщо частка влітає в магнітне поле й при цьому вектор швидкості   перпендикулярний вектору  , то sinα = 90°, F_Л = qvB. Т.к.   перпендикулярна швидкості  , то   буде доцентрової силою, а рух частки буде відбуватися по окружності, центр якої збігається з однієї із силових ліній вектора 

 

 

 

 

.

1. Заряджена частка влітає в магнітне поле під довільним кутом до силових ліній вектора : 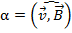 . Частка буде рухатися по гвинтовій лінії (по спіралі). У цьому випадку швидкість частки можна розкласти на дві складов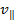і   і 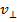 , а рух по спіралі розглядати як суму двох рухів: рух по окружності зі швидкістю і прямолінійний рух уздовж силової лінії  зі швидкістю  .

    .

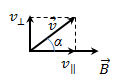
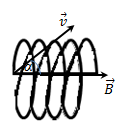
Визначимо радіус і крок гвинта:

.

Період спирали:

 

Крок спирали:  

 

Закон Ампера для циркуляції магнітного поля — твердження про те, що інтеграл по замкненому контуру від магнітної індукції пропорційний силі електричному струму, що протікає через площу, обмежену контуром. Закон сформулював у 1826 році Андре-Марі Ампер. У модифікованому вигляді він входить до основних рівнянь електродинаміки.

Наслідком закону Ампера є те, що струми, які протікають за межами контура, не дають внеску в циркуляцію.

Зміст   [сховати]  1 Формулювання 1.1 Інтегральна форма 1.2 Диференційна форма 2 Модифікація з врахуванням змінного електричного поля 3 У середовищі 4 Джерела

[ред.]Формулювання

[ред.]Інтегральна форма

У системі одиниць СГС закон Ампера має вигляд:

,

де   — магнітна індукція,   — густина струму,   - швидкість світла.

У СІ :

,

де   — магнітна стала.

Закон справедливий для постійних струмів і полів. У разі змінних струмів в формулі з'являється член, пов'язаний із струмом зміщення.

[ред.]Диференційна форма

В диференційній формі закон Ампера набирає вигляду (СГС):

або (СІ)

[ред.]Модифікація з врахуванням змінного електричного поля

Змінне електричне поле є додатковим джерелом, що породжує магнітне поле. З його врахуванням закон Ампера змінює форму. Для вакууму він набирає вигляду (СГС):

,

де   — напруженість електричного поля. Величину

де   - вектор електричної індукції, називають струмом зміщення. Для вакууму  .

[ред.]У середовищі

Закон Ампера для циркуляції магнітного поля можна використовувати також і для середовища, однак при цьому потрібно враховувати всі струми, які виникають у середовищі. Це не тільки струми вільних зарядів, а струми зарядів, зв'язаних в складі атомів і молекул. Такі струми виникають з двох причин. По-перше, зв'язаніелектрони в магнітному полі прецесують, створюючи струм намаганіченння, по-друге, у випадку змінного електричного поля, електрони зміщуються відносно йонів, з якими вони зв'язані, створюючи струм поляризації. Враховуючи всі ці струми закон Ампера для середовища, записують в такій формі, щоб у ньому залишилися тільки струми вільних заряджених частинок:

,

де   - напруженість магнітного поля,   — струм вільних зарядів. При цьому внесок струмів намагнічування входить у визначення  , а внесок струмів поляризації — у визначення  .

У диференційній формі закон Ампера набирає вигляду (СГС):