Лабораторная работа № 9 Численное интегрирование (Методы левых, правых, средних прямоугольников и метод трапеций)
Постановка задачи:
Необходимо найти
интеграл
.
Из курса математического анализа известна формула Ньютона-Лейбница:
Функция f(x) непрерывна на отрезке [a;b], однако в большинстве случаев первообразную F(x) для подынтегральной f(x) не удаётся выразить через элементарные функции (т. е. существуют неберущиеся точными методами интегралы). Кроме того подынтегральная функция может быть задана не функцией, а таблицей, поэтому необходимы численные методы интегрирования.
К ним относятся методы прямоугольников (левых, правых и средних), метод трапеций и метод парабол (Симпсона). Метод парабол мы рассматривать не будем.
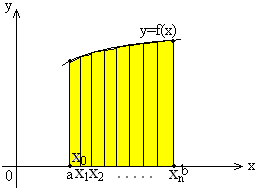
Из геометрического смысла определённого интеграла следует, что он равен площади (S) криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми x=a, x=b и осью Ox.
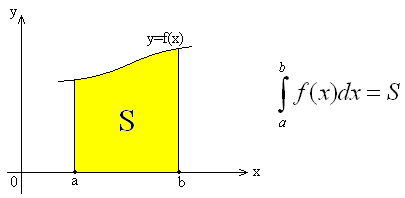
Заменим данную криволинейную трапецию прямоугольником с шириной b-a и высотой f(a) (метод левых прямоугольников), f(b) (метод правых прямоугольников), f(c) (метод средних прямоугольников).
Метод левых прямоугольников:
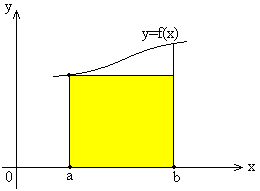
Ширина b-a, высота f(a).
Метод правых прямоугольников:
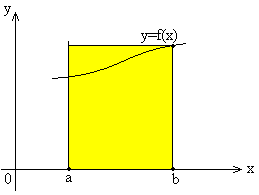
Ширина b-a, высота f(b).
Метод средних прямоугольников:
Ширина b-a, высота f(c).
Для минимизации погрешности, полученной при такой замене фигур, отрезок [a;b] делят на n-равных частей и каждую из частей исходной трапеции заменяют левым, правым или средним прямоугольником.
Метод левых прямоугольников:
Криволинейная трапеция при этом заменена ступенчатой фигурой, площадь (S) которой равна сумме площадей прямоугольников.
x0=a, n – количество разбиений.
Метод правых прямоугольников:
xn=b.
Метод средних прямоугольников:
,
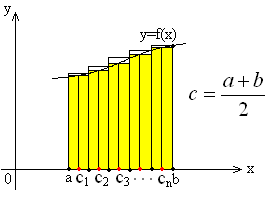
где
часто обозначают
h
(шаг интегрирования).
Для метода левых прямоугольников x=x+h.
Для метода правых прямоугольников x=а+h.
Для метода средних
прямоугольников
.
Метод трапеций:
Идея метода – замена криволинейной трапеции на прямоугольную.
Для минимизации погрешности отрезок [a;b] делится на n-равных частей, а криволинейная трапеция заменяется фигурой, состоящей из n-прямоугольных трапеций, имеющих одинаковые высоты , а основания равны f(xi).
Тогда
Исходные данные:
Алгоритм решения:
1) Ввод a, b, eps.
2) Задать n=1.
3) Вычисляем I1=metleft(n,a,b);
4) n=n+1.
5) I2=metleft(n,a,b);
6) d=|I2-I1| расстояние между двумя вычисляемыми интегралами
7) Если d>eps,
тогда I1=I2,
идти к 4 шагу
8) Вывод I2, n.
Текст программы:
#include<conio.h>
#include<math.h>
#include<iostream.h>
float f(float x)
{
return (pow(M_E,x)*sin(x*x));
}
float metlev(float a, float b, int n)
{
float h=(b-a)/n, x=a, sum=0;
for(float i=1;i<=n;i++)
{
sum+=f(x);
x+=h;
}
return h*sum;
}
float metprav(float a, float b, int n)
{
float h=(b-a)/n, x=a, sum=0;
for(int i=0;i<n;i++)
{
sum+=f(x);
x+=h;
}
return h*sum;
}
float metsred(float a, float b, int n)
{
float h=(b-a)/n, x=a, sum=0;
for(int i=0;i<n;i++)
{
sum+=f((x+x+h)/2);
x+=h;
}
return h*sum;
}
float mettrap(float a, float b, int n)
{
float h=(b-a)/n, x=a, sum=0;
for(float i=1;i<n;i++)
{
sum+=f(x);
x+=h;
}
sum+=f(a); sum+=f(b);
return h*sum;
}
void main(void)
{
int n=1;
float I1, I2, Eps, a, b;
clrscr(); textmode(2);
cout<<"Integral: pow(M_E,x)*sin(x*x)\n\nVvod a, b, Eps: ";
cin>>a>>b>>Eps;
do
{
I1=metlev(a,b,n);
n++;
I2=metlev(a,b,n);
}
while((fabs(I1-I2)>Eps)&&!kbhit());
cout<<"\nMetod levyx pryamougolnikov\nIteraziy: "<<n<<"\nOtvet: "<<I2;
n=1;
do
{
I1=metprav(a,b,n);
n++;
I2=metprav(a,b,n);
}
while((fabs(I1-I2)>=Eps)&&!kbhit());
cout<<"\n\nMetod pravyx pryamougolnikov\nIteraziy: "<<n<<"\nOtvet: "<<I2;
n=1;
do
{
I1=metsred(a,b,n);
n++;
I2=metsred(a,b,n);
}
while((fabs(I1-I2)>=Eps)&&!kbhit());
cout<<"\n\nMetod srednix pryamougolnikov\nIteraziy: "<<n<<"\nOtvet: "<<I2;
n=1;
do
{
I1=mettrap(a,b,n);
n++;
I2=mettrap(a,b,n);
}
while((fabs(I1-I2)>=Eps)&&!kbhit());
cout<<"\n\nMetod trapeziy\nIteraziy: "<<n<<"\nOtvet: "<<I2;
getch();
}
Скриншот результата программы (при Eps=0, 01):
Результаты работы программы:
Если сравнить результаты интегрирования функции методом левых, правых, средних прямоугольников и методом трапеций, то результаты почти совпадают (схожи).
Скриншот результата программы (при Eps=0, 00001):
Результаты работы программы:
Если сравнить результаты интегрирования функции методом левых, правых, средних прямоугольников и методом трапеций, то результаты почти совпадают (схожи).
Чем меньше Eps, тем больше итераций требуется для достижения результата, и тем точнее он получается.