Лабораторная работа № 6 Аппроксимация табличной функции методом неопределённых коэффициентов (методом Вандермонда)
Постановка задачи:
Пусть величина y является некоторой функцией аргумента x, но её невозможно записать в виде некоторой формулы, или эта формула очень громоздка и трудна в работе, но при этом задана таблица:
узлы
-
. . .
значение
функции
в этих узлах
. . .
В
водим
некоторое
,
.
Необходимо найти приближённое значение этой функции в некоторой точке x.
Аппроксимировать функцию, значит неизвестную функцию y=f(x), заданную таблицей, требуется заменить некоторой приближённой (аппроксимирующей) функцией Pn(x) (полиномом) так, чтобы отклонение f(x) от Pn(x) было минимальным в заданной области.
Аппроксимация, при которой приближение строится на некотором разрывном множестве точек, называется точечной. А на непрерывном (например, на отрезке) называется непрерывной.
Одним из основных способов точечной аппроксимации является интерполирование. Это вычисление приближённого значения функции в некоторой точке .
А экстраполяция
- это вычисление приближённого значения
функции в некоторой точке
.
В виде аппроксимирующей
функции будем рассматривать многочлен
(полином)
.
Полином должен проходить через заданную систему точек.
Б
удем
подставлять в него поочерёдно вместо
x x0,
x1 . . . xn,
а вместо Pn(x)
y0, y1
. . . yn.
Получим систему, состоящую из n+1
– уравнения с n+1 –
неизвестным коэффициентом a0,
a1 . . . an.
|
|
|
|
.......... |
|
|
|
|
|
(1)
Решаем эту систему линейных уравнений любым численным методом (методом Гаусса, методом Зейделя или методом простых итераций) (1, 2 и 3 лабораторные работы).
Найденные коэффициенты a0, a1 . . . an подставляем в аппроксимирующую функцию (1).
А затем подставляем вместо х данное значение и вычисляем значение функции.
Вспомогательная матрица Вандермонда:
An=
одномерный массив неизвестных
Yn=
массив данных
Исходные данные:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция для проверки: y=tg(cos(x)).
Алгоритм решения:
1) Задать N – количество узлов данных
2) Задать исходные данные к задаче:
float X[N] = {.., .., .., ..,};
3) float Y[N] = {.., .., .., ..,};
4) Формирование матрицы Вандермонда:
н. ц. i = 0, n
Wi0=1
н. ц. j = 1, n
Wij = Wij-1*Xi
к. ц. j
к. ц. i
5) Решение системы:
Wnxn*An=Yn
6) Ввод z (x).
7) Подставляем
P=0
н. ц. i = 0, n
P=P+ai*pow(z,i)
к. ц. i
8) Вывод P.
9) Проверка:
y=f(z)
Текст программы:
#include<iostream.h>
#include<math.h>
#include<stdio.h>
#include<conio.h>
float *X,*Y,**V;
float *B,*R,h,z;
int n,i,j,k,p=0;
void init(int q=1)
{
if(q)
{X=new float [n];
Y=new float [n];
V=new float *[n];
for(i=0;i<n;i++) V[i]=new float[n];
B=new float [n];
R=new float [n]; for(i=0;i<n;i++) R[i]=0;}
else
{delete[] X;
delete[] Y;
for(i=0;i<n;i++) delete[] V[i]; delete[] V;
delete[] B;
delete[] R;}
}
void ex(void)
{
n=8;
p=1;
init(1);
float X1[8]={0.1, 0.3, 0.5, 0.7, 0.9, 1.1, 1.3, 1.5};
float Y1[8]={1.540, 1.414, 1.204, 0.960, 0.716, 0.487, 0.274, 0.017};
cout<<"\nVvod x[8]: ";
for(i=0;i<n;i++)
{
X[i]=X1[i];
printf("%.1f ",X[i]);
}
cout<<"\n\nVvod y[8]: ";
for(i=0;i<n;i++)
{
Y[i]=Y1[i];
printf("%.3f ",Y[i]);
}
cout<<endl<<endl;
}
void wander(void)
{
for(i=0;i<n;i++)
{
V[i][0]=1;
for(j=1;j<n;j++)
V[i][j]=V[i][j-1]*X[i];
}
}
void gaus(void)
{
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
{
h=V[j][i]/V[i][i];
for(k=0;k<n;k++)
V[j][k]=V[j][k]-h*V[i][k];
Y[j]=Y[j]-h*Y[i];
}
R[n-1]=Y[n-1]/V[n-1][n-1];
for(i=n-2;i>=0;i--)
{
h=Y[i];
for(j=i+1;j<n;j++)
h=h-R[j]*V[i][j];
R[i]=h/V[i][i];
}
}
float P(float x)
{
float p=0;
for(i=0;i<n;i++) p+=pow(x,i)*R[i];
return p;
}
void main(void)
{
clrscr();
textmode(2);
cout<<"Vvod 0 "; gotoxy(10,1); cin>>n;
if(n<=0) ex(); else
{
init();
cout<<"Vvod x["<<n<<"] ";
for(i=0;i<n;i++)
cin>>X[i];
cout<<"Vvod n["<<n<<"] ";
for(i=0;i<n;i++)
cin>>Y[i];
}
wander();
gaus();
cout<<"Vvod x: "; cin>>z;
cout<<"\nf("<<z<<")="<<P(z);
if(p) cout<<"\n\nProverka: tg(cos("<<z<<"))="<<sin(cos(z))/cos(cos(z));
init(0);
getch();
}
Скриншот результата программы (при x=0, 4):
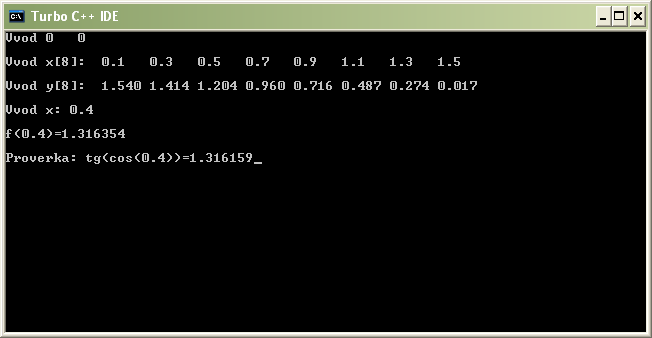
Результаты работы программы и проверка (проверка говорит о том, что решение правильное):
f(0, 4) = 1, 316354