Лабораторная работа № 4.2 Решение нелинейных уравнений методом хорд
Постановка задачи:
Необходимо решить уравнение f(x)=0 с заданной точностью, если на отрезке
функция f(x) непрерывна, монотонна и имеет разные знаки на концах ( ). На этом отрезке существует и единственен корень исходного уравнения.
II этапа решения данной задачи:
I этап: отделение корней
Получение отрезка [a;b], содержащего единственное решение.
Проводим хорду через концы графика и находим абсциссу точки пересечения её с осью x (c1), находим значение функции в точке с1 (определяем знак функции в точке с1), сравниваем знаки функций в точке а, b, c1, присваиваем с1 в a или b (так, чтобы знаки совпадали).
Проводим новую хорду, поступаем аналогично до тех пор, пока не будет выполнено одно из условий: |f(c)|<Eps или |b-a|<Eps.
II этап: численные методы (метод хорд)
Алгоритм решения:
1) Ввод a, b, Eps
2) iter
do
2.1. Получение точки пересечения хорды с осью X
iter++
2.2. если
b=c
иначе a=c
while (|f(c)|<Eps или |b-a|<Eps)
3) Вывод решения – с
4) Проверка (подставляем в функцию с, f(c) должно получиться ≈ 0 )
Исходные данные:
График функции:
По графику видно, что отрезок [a;b] – это [0,1], т. к. на этом отрезке у графика разные знаки на концах.
Текст программы:
#include<conio.h>
#include<iostream.h>
#include<math.h>
long double f(long double x)
{
if (x==0) x=0.000001;
return (2*log(x)-x/2+1) ;
}
void main()
{
clrscr();
long double a, b, Eps, c=0;
int iter=0;
cout<<"Vvedite a, b, Eps ";
cin>>a>>b>>Eps;
do
{
c=(f(a)*(b-a))/(f(a)-f(b))+a;
if (f(a)*f(c)<0) b=c;
else a=c;
iter++;
}
while(fabs(f(c))>Eps);
cout<<"\nOtvet: "<<c<<"\n\nIteraziy: "<<iter<<"\n\nProverka: "<<f(c);
getch();
}
Скриншот результата программы (при Eps=0,001 100 итераций):
Результаты работы программы (проверка говорит о том, что решение правильное – f(c) ≈ 0):
с ( )=0, 727944
Скриншот результата программы (при Eps=0,00000001 282 итерации):
Результаты работы программы (проверка говорит о том, что решение правильное – f(c) ≈ 0):
с ( )=0, 727514
Если сравнить результаты решения нелинейных уравнений методом деления отрезка пополам и методом хорд, то результаты почти совпадают.
Чем меньше Eps, тем больше итераций требуется для достижения результата, и тем точнее он получается.
Лабораторная работа № 5 Решение нелинейных уравнений методом Ньютона
Постановка задачи:
Необходимо решить уравнение f(x)=0 с заданной точностью, если на отрезке
функция f(x) непрерывна, монотонна и имеет разные знаки на концах ( ).
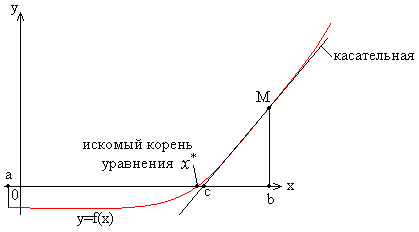
Через точку М
проводим касательную к графику y=f(x),
находим пересечение её с осью Х – с,
строим перпендикуляр из точки с к
графику, проводим новую
касательную,
поступаем аналогично до тех пор, пока
не будет выполнено одно из условий:
или
.
Для реализации метода необходимо решить следующие задачи:
1) Получение (выбор)
начального приближения -
2) Формула метода Ньютона:
3) Условия завершения итерационного процесса:
1.
2.
Алгоритм решения:
1) Ввод a, b, Eps
2) Выбор x0
если
тогда Xk=a
иначе Xk=b
3) iter++
4) Итерационный процесс:
do
4.1) iter++
4.2)
4.3) d=|XK1-XK|
4.4) если d > Eps, тогда XK=XK1
условие продолжения:
while (d > Eps)
5) Вывод результатов: XK1 и iter
6) Проверка: f(XK1) ≈ Eps
Исходные данные:
График функции:
По графику видно, что отрезок [a;b] – это [0,1], т. к. на этом отрезке у графика разные знаки на концах.
Текст программы:
#include <conio.h>
#include <math.h>
#include <iostream.h>
long double f(long double x)
{
if (x==0) x=0.000001;
return (2*log(x)-x/2+1);
}
long double f1(long double x)
{
if (x==0) x=0.000001;
return ((4-x)/(2*x));
}
long double f2(long double x)
{
return ((-2)/pow(x,2));
}
void main()
{
clrscr();
long double a, b, Eps, c=0;
int iter=0;
cout<<"Vvedite a, b, Eps ";
cin>>a>>b>>Eps;
if(f(a)*f1(a)>0) c=a;
else c=b;
do
{
c-=f(c)/f1(c);
iter++;
}
while(fabs(f(c))>Eps);
cout<<"\nOtvet: "<<c<<"\n\nIteraziy: "<<iter<<"\n\nProverka: "<<f(c);
getch();
}
Скриншот результата программы (при Eps=0,1 2 итерации):
Результаты работы программы (проверка говорит о том, что решение правильное – f(c) ≈ 0):
с ( )=0, 724372
Скриншот результата программы (при Eps=0,0000000001 5 итераций):
Результаты работы программы (проверка говорит о том, что решение правильное – f(c) ≈ 0):
с ( )=0, 727514
Если сравнить результаты решения нелинейных уравнений методом деления отрезка пополам, методом хорд и методом Ньютона, то результаты почти совпадают.
Чем меньше Eps, тем больше итераций требуется для достижения результата, и тем точнее он получается.