Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Прикарпатский национальный университет им. В. Стефаника

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Laboratornye_raboty_po_chislennym_metodam.doc

Скачиваний:

Добавлен:

01.03.2025

Размер:

910.34 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Лабораторная работа № 3 Решение систем линейных уравнений методом Зейделя

Постановка задачи:

Дана система линейных уравнений:



	..........

Необходимо решить систему линейных уравнений методом Зейделя.

Метод Зейделя является ускоренной разновидностью метода простых итераций.

Для реализации метода необходимо решить следующие задачи:

1) Проверка условия сходимости:

2) Получить итерационную зависимость (нахождение следующего приближения через предыдущее):

3) Выбор начального приближения:

1) 0 – одномерный нулевой массив

2) G_n

4) Условия завершения вычислений:

разность двух соседних итераций меньше Eps



	. . . . . . . . . .



	. . . . . . . . . .

Исходные данные:

Алгоритм решения:

1) Проверка условия сходимости:

2) Ввод исходных данных:

A_nxn, В_n, Eps

3) Сформировать матрицы R_nxn и G_n:

н. ц. i = 1, n

н. ц. j = 1, n

если i=j, то r_ij=0

иначе

к. ц. j

к. ц. i

4) Задание начального приближения:

н. ц. i = 1, n

(0)

к. ц. i

5) Итерационный процесс:

kol=0

н. ц. i = 1, n

XK1_i=0

н. ц. j = 1, n

если i<j, тогда

иначе i>j, тогда

к. ц. j

XK1_i=XK1_i+G_i

к. ц. i

н. ц. i = 1, n

d_i=|XK1_i-XK_i| получение вектора d

к. ц. i

max из d_n

если max > Eps, тогда

н. ц. i=1, n

XK_i= XK1_i

к. ц. i

kol++

while (max > Eps)

6) Вывод результата – XK1, kol (количество итераций)

7) Проверка результата:

XK1 подстав. в исходную систему

Текст программы:

#include<iostream.h>

#include<math.h>

#include<conio.h>

float **A,*B,h,*X,**a,*r,**R,*G,*XK,*XK1,*D; int n;

void init(int q)

{

int i;

if(q)

{

A=new float *[n]; for(i=0;i<n;i++) A[i]=new float[n];

B=new float [n];

X=new float [n]; for(i=0;i<n;i++) X[i]=0;

a=new float *[n]; for(i=0;i<n;i++) a[i]=new float[n];

r=new float [n]; for(i=0;i<n;i++) r[i]=0;

R=new float *[n]; for(i=0;i<n;i++) R[i]=new float[n];

G=new float [n];

XK=new float [n];

XK1=new float [n];

D=new float [n];

}

else

{

for(i=0;i<n;i++) delete[] A[i]; delete[] A;

delete[] B;

delete[] X;

for(i=0;i<n;i++) delete[] a[i]; delete[] a;

delete[] r;

for(i=0;i<n;i++) delete[] R[i]; delete[] R;

delete[] G;

delete[] XK;

delete[] XK1;

delete[] D;

}

void ex(void)

{

init(1);

float A1[4][4]={-0.12,1.00,-0.32,0.18, //исходные данные

0.77,0.14,-0.06,0.12,

-0.25,-0.22,-0.14,1.00,

-0.08,0.12,0.77,-0.32};

float B1[4]={-0.72,1.21,0.56,-0.58};

cout<<"\nVvod A[4][4]:\n\n";

for(int i=0;i<n;i++)

{for(int j=0;j<n;j++)

{A[i][j]=A1[i][j]; //копируем в А

cout<<A[i][j]<<" ";}

cout<<"\n";}

cout<<"\nVvod B[4]:\n\n";

for(i=0;i<n;i++)

{B[i]=B1[i];

cout<<B[i]<<" ";}

cout<<"\n";}

float shdm(int t)

{

float tp=0;

for(int j=0;j<n;j++)

if(j!=t) tp+=A[t][j];

return tp;

}

void swap(int a, int b)

{

float tp,rt;

for(int i=0;i<n;i++)

{

tp=A[a][i];

A[a][i]=A[b][i];

A[b][i]=tp;

}

rt=B[a]; B[a]=B[b]; B[b]=rt;

}

//cout<<"\nswap OK\n";

float maxd(void)

{

float mx;

mx=D[0];

for(int i=1;i<n;i++) if(D[i]>mx) mx=D[i];

return mx;

}

void main(void)

{

int i,j,k,col=0;

float max,eps;

textmode(2); clrscr();

cout<<"Vvod n (0)"; gotoxy(9,1); cin>>n; //выводит текущий пример по 0 if(n==0) или задаём размер и вводим

{ матрицы

n=4;

ex();

}

else

{

init(1);

cout<<"Vvod A["<<n<<"]["<<n<<"]:\n";

for(i=0;i<n;i++)

for(j=0;j<n;j++)

cin>>A[i][j];

cout<<"\n";

cout<<"Vvod B["<<n<<"]:\n";

for(i=0;i<n;i++)

cin>>B[i];

}

int *y=new int[3];

y[2]=0;

for(j=0;j<n;j++)

for(i=0;i<n;i++)

if(A[i][i]<shdm(i))

{y[y[2]]=i; y[2]++;

if(y[2]>=2)

{swap(y[0],y[1]); y[2]=0;}

}

delete[] y;

for(i=0;i<n;i++)

for(j=0;j<n;j++)

a[i][j]=A[i][j];

for(i=0;i<n;i++)

{

for(j=0;j<n;j++)

{

if(i!=j) R[i][j]=(-A[i][j]/A[i][i]); else R[i][j]=0;

}

G[i]=B[i]/A[i][i];

}

for(i=0;i<n;i++)

{

XK[i]=G[i];

}

cout<<"\nVvod E: "; cin>>eps;

{

for(i=0;i<n;i++)

{

XK1[i]=0;

for(j=0;j<n;j++)

{

if(i<j) XK1[i]+=(R[i][j]*XK[j]);

else if(i>j) XK1[i]+=(R[i][j]*XK1[j]);

}

XK1[i]+=G[i];

}

for(i=0;i<n;i++)

D[i]=fabs(XK1[i]-XK[i]);

max=maxd();

if(max>=eps)

for(i=0;i<n;i++)

XK[i]=XK1[i];

col++;

}

while(max>=eps&&!kbhit());

cout<<"\nIteraziy: "<<col<<"\n";

cout<<"\nResenie:\n\n";

for(i=0;i<n;i++)

cout<<XK1[i]<<" ";

cout<<"\n\nProverka:\n\n";

for(i=0;i<n;i++)

{

for(int j=0;j<n;j++)

r[i]+=(a[i][j]*XK1[j]);

cout<<r[i]<<" ";

}

getch();

init(0);

}

Скриншот результата программы (при Eps=0,01 4 итерации):

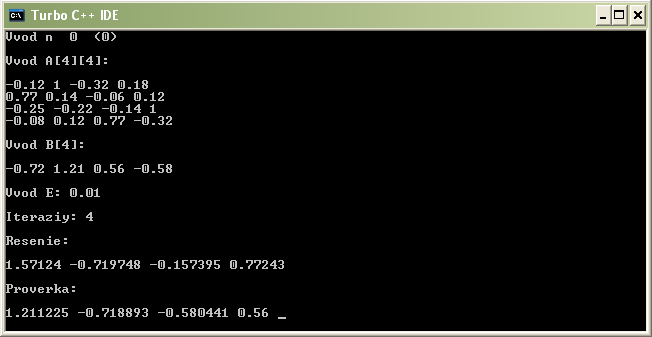
Результаты работы программы (проверка говорит о том, что решение правильное):

x₁ = 1, 57124

x₂ = - 0, 719748

x₃ = - 0, 157395

x₄ = 0, 77243

Если сравнить результаты решения систем линейных уравнений методом Гаусса, методом простых итераций и методом Зейделя, то результаты почти совпадают.

Скриншот результата программы (при Eps=0, 0000001 14 итераций):

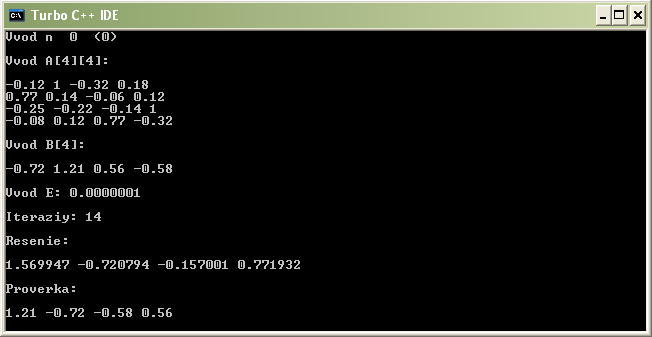
Результаты работы программы (проверка говорит о том, что решение правильное):

x₁ = 1, 569947

x₂ = - 0, 720794

x₃ = - 0, 157001

x₄ = 0, 771932

Чем меньше Eps, тем больше итераций требуется для достижения результата, и тем точнее он получается.

Лабораторная работа № 4

Решение нелинейных уравнений методом деления отрезка пополам и методом хорд

Лабораторная работа № 4.1

Решение нелинейных уравнений методом деления отрезка пополам

Постановка задачи:

Необходимо решить уравнение f(x)=0 с заданной точностью, если на отрезке

функция f(x) непрерывна, монотонна и имеет разные знаки на концах ( ).

Уравнение называется нелинейным, потому что оно может содержать тригонометрические, логарифмические, показательные функции, и потому что x могут входить в степень выше первой.

Разделим отрезок [a;b] пополам, найдя его середину ( ), определим знак f(c), если он совпадает со знаком f(b), то с присваиваем в b, если нет, то в a, и опять находим середину уменьшенного в 2 раза отрезка до тех пор, пока не будет выполнено одно из условий (|f(c)|<Eps или |b-a|<Eps).

II этапа решения данной задачи:

I этап: отделение корней

Получение отрезка [a;b], содержащего единственное решение.

II этап: численные методы (метод деления отрезка пополам)

Алгоритм решения:

1) Ввод a, b, Eps

2) Цикл

iter

2.1. Получение середины отрезка

iter++

2.2. если

b=c

иначе a=c

while (|f(c)|<Eps или |b-a|<Eps)

3) Вывод решения – с

4) Проверка (подставляем в функцию с, f(c) должно получиться ≈ 0 )

Исходные данные:

График функции:

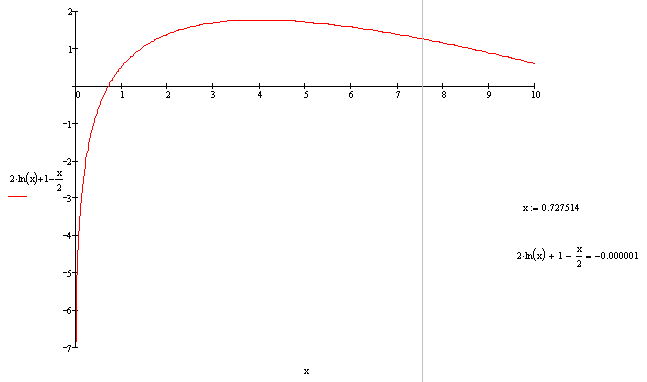
По графику видно, что отрезок [a;b] – это [0,1], т. к. на этом отрезке у графика разные знаки на концах.

Текст программы:

#include<conio.h>

#include<iostream.h>

#include<math.h>

long double f(long double x)

{

if (x==0) x=0.000001;

return (2*log(x)-x/2+1) ;

}

void main()

{

clrscr();

long double a, b, Eps, c=0;

int iter=0;

cout<<"Vvedite a, b, Eps ";

cin>>a>>b>>Eps;

{

c=(a+b)/2;

if (f(a)*f(c)<0) b=c;

else a=c;

iter++;

}

while(fabs(f(c))>Eps);

cout<<"\nOtvet: "<<c<<"\n\nIteraziy: "<<iter<<"\n\nProverka: "<<f(c);

getch();

}

Скриншот результата программы (при Eps=0,01 7 итераций):

Результаты работы программы (проверка говорит о том, что решение правильное – f(c) ≈ 0):

с ( )=0, 726562

Скриншот результата программы (при Eps=0,0000001 22 итерации):

Результаты работы программы (проверка говорит о том, что решение правильное – f(c) ≈ 0):

с ( )=0, 727515

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2016447.49 Кб19Laboratorna_robota_1.doc
#
14.02.2016151.04 Кб5Laboratorna_robota_5_2014-2015_I_s_doc.doc
#
01.04.2025872.45 Кб0LABORATORNA_ROBOTA_6_II_sem..doc
#
14.02.20162.75 Mб13Laboratorna_robota_OA-11.doc
#
14.02.20161.9 Mб21laboratorni_roboti_1-14_a.pdf
#
01.03.2025910.34 Кб0Laboratornye_raboty_po_chislennym_metodam.doc
#
14.02.2016135.31 Кб11LAB_04.pdf
#
14.02.2016252.91 Кб14LAB_06.pdf
#
14.02.2016157.29 Кб60LAB_07 .pdf
#
01.05.2025372.22 Кб0Lab_2.doc
#
01.05.2025280.58 Кб0Lab_3.doc