Комитет по образованию Правительства Санкт-Петербурга

Санкт-петербургский колледж информационных технологий Лабораторные работы по численным методам

(Вариант № 15)

Выполнила

студентка группы № 81 СПбКИТ

Мясникова Ольга

Преподаватель

Матысик И. А.

2010

№	Тема	Дата	Оценка	Подпись преподавателя
	Решение нелинейных уравнений методом деления отрезка пополам

Лабораторная работа № 1 Решение систем линейных уравнений методом Гаусса

Постановка задачи:

Дана система линейных уравнений:

	..........

Данная система называется линейной, потому что она не содержит тригонометрических, логарифмическиx, показательныx функций, и потому что x входят в степень не выше первой.

Необходимо решить систему линейных уравнений методом Гаусса, т. е. привести матрицу коэффициентов к треугольному виду (прямой ход), выразить и найти неизвестные – x_n (обратный ход).

Иначе систему можно записать так: A_nxn* X_n = B_n

A_nxn – двумерный массив

X_n и B_n – одномерные массивы

I этап – Прямой ход:

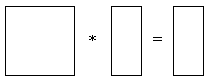
A_nxn X_n B_n Преобразование к треугольному виду

A’_nxn X’_n B'_n

II этап – Обратный ход:

A’_nn* X_n = B'_n

X_n = B’_n / A’_nn

Исходные данные:

Алгоритм решения:

1) Задать N – количество уравнений в системе

2) Задать исходные данные к задаче:

float A[N][N] = {{.., .., .., ..,},

{.., .., .., ..,},

{.., .., .., ..,},

{.., .., .., ..,}};

float B[N] = {.., .., .., ..,};

3) Реализация метода Гаусса:

Прямой ход:

н. ц. i = 1, n

н. ц. j = i + 1, n

h = a_ji / a_ii

н. ц. k = 1, n

a_jk = a_jk – h*a_ik

к. ц. k

b_j = b_j – h*b_i

к. ц. j

к. ц. i

Обратный ход: X_n = B_n / A_nn

н. ц. i = n – 1, 1

float h = b_i

н. ц. j = i + 1, n

h = h – x_j*a_ij

к. ц. j

x_i = h / a_ii

к. ц. i

5) Вывод результатов решений (X_n).

6) Проверка результатов.

Текст программы:

#include<conio.h>

#include<iostream.h>

float **A,*B, h, *X, **a, *q;

int n;

void main(void)

{

int i, j, k;

clrscr();

cout<<"Vvod 0 (n=) "; cin>>n; //выводит текущий пример по 0 или задаём

if(n==0) размер и вводим матрицы

{

n=4;

A=new float *[n]; for(i=0;i<n;i++) A[i]=new float[n];

B=new float [n];

X=new float [n]; for(i=0;i<n;i++) X[i]=0;

a=new float *[n]; for(i=0;i<n;i++) a[i]=new float[n];

q=new float [n]; for(i=0;i<n;i++) q[i]=0;

float A1[4][4]={-0.12,1.00,-0.32,0.18, //исходные данные

0.77,0.14,-0.06,0.12,

-0.25,-0.22,-0.14,1.00,

-0.08,0.12,0.77,-0.32};

float B1[4]={-0.72,1.21,0.56,-0.58};

cout<<"\nVvod A[4][4]:\n\n";

for(int i=0;i<n;i++)

{

for(int j=0;j<n;j++)

{A[i][j]=A1[i][j]; //копируем в A

cout<<A[i][j]<<" ";}

cout<<"\n";}

cout<<"\nVvod B[4]:\n\n";

for(i=0;i<n;i++)

{B[i]=B1[i];

cout<<B[i]<<" ";}

cout<<"\n";}

else

{

A=new float *[n]; for(i=0;i<n;i++) A[i]=new float[n];

B=new float [n];

X=new float [n]; for(i=0;i<n;i++) X[i]=0;

a=new float *[n]; for(i=0;i<n;i++) a[i]=new float[n];

q=new float [n]; for(i=0;i<n;i++) q[i]=0;

cout<<"\nVvod A["<<n<<"]["<<n<<"]:\n\n";

for(i=0;i<n;i++)

for(j=0;j<n;j++)

cin>>A[i][j];

cout<<"\n";

cout<<"\nVvod B["<<n<<"]:\n\n";

for(i=0;i<n;i++)

cin>>B[i];}

for(i=0;i<n;i++)

for(j=0;j<n;j++)

a[i][j]=A[i][j]; //копирует А в а, чтобы потом сделать проверку

for(i=0;i<n;i++) //прямой ход - приводим к треугольному виду

for(j=i+1;j<n;j++)

{h=A[j][i]/A[i][i];

for(k=0;k<n;k++)

A[j][k]=A[j][k]-h*A[i][k];

B[j]=B[j]-h*B[i];}

cout<<"\n";

for(i=n-1;i>=0;i--) //обратный ход - находим решение

{h=B[i];

for(j=i+1;j<n;j++)

h=h-X[j]*A[i][j];

X[i]=h/A[i][i];}

cout<<"Resenie:\n\n";

for(i=0;i<n;i++)

cout<<X[i]<<" ";

cout<<"\n";

cout<<"\nProverka:\n\n";

for(i=0;i<n;i++)

{for(int j=0;j<n;j++)

q[i]+=(a[i][j]*X[j]);

cout<<q[i]<<" ";}

for(i=0;i<n;i++) delete[] A[i]; delete[] A; //освобождает место в

delete[] B; оперативной памяти

delete[] X;

for(i=0;i<n;i++) delete[] a[i]; delete[] a;

delete[] q;

getch();

}

Скриншот результата программы:

Результаты работы программы и проверка:

x₁ = 1, 569947

x₂ = - 0, 720794

x₃ = - 0, 157001

x₄ = 0, 771932