
- •Справочный материал для подготовки к интернет-тестированию по курсу «математика»
- •Содержание
- •Комплексные числа
- •2. Матрицы и системы линейных алгебраических уравнений (слау)
- •3. Векторная алгебра
- •4. Аналитическая геометрия
- •5. Теория пределов. Дифференциальное исчисление
- •6. Интегральное исчисление
- •7. Дифференциальные уравнения (ду)
- •8. Ряды
- •9. Теория вероятностей
- •10. Математическая статистика
- •11. Математические модели в экономике
- •Литература
- •Справочный материал для подготовки к интернет-тестированию
6. Интегральное исчисление
![]() — первообразная
для
— первообразная
для
![]() ,
если
,
если
![]() ;
;
![]()
![]()
![]()
![]()
![]()
![]() ;
;

![]()
![]()


![]() EMBED
Equation.DSMT4
EMBED
Equation.DSMT4
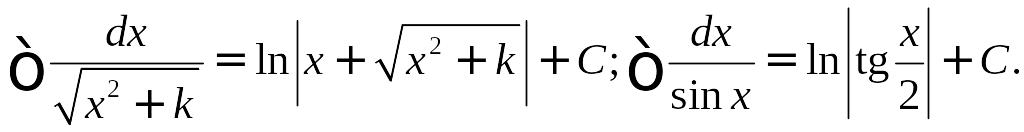
![]()
 .
.
![]() ;
;
![]() .
.
7. Дифференциальные уравнения (ду)
Решение ДУ — дифференцируемая функция, обращающая ДУ в верное тождество.
Порядок ДУ — порядок старшей производной (старшего дифференциала) в данном уравнении.
Задача
Коши для
ДУ 1-го порядка вида
![]() :
найти частное решение ДУ,
удовлетворяющее
условию
:
найти частное решение ДУ,
удовлетворяющее
условию
![]() ,
где
,
где
![]() — заданные числа.
— заданные числа.
Типы ДУ 1-го порядка:
а)
с
разделяющимися переменными:
![]()
или
![]() (решается
разделением переменных:
(решается
разделением переменных:
![]() …);
…);
б)
однородное
(в
однородных функциях):
![]() или
или
![]() ,
где
,
где
![]() — однородные функции одинаковой степени
однородности (решается
заменой
— однородные функции одинаковой степени
однородности (решается
заменой
![]()
![]() );
);
 в)
линейное
неоднородное:
в)
линейное
неоднородное:![]()
г)
типа Бернулли:
![]()
(решаются методом Бернулли сведением к двум ДУ с разделяющимися
переменными
для функций
![]() :
:![]() …).
…).
Линейное ДУ 2-го порядка с постоянными коэффициентами:
![]() (однородное,
если
(однородное,
если
![]() ,
и неоднородное,
если
,
и неоднородное,
если
![]() ).
).
Общее
решение неоднородного ДУ:
![]() ,
где
,
где
![]() — общее решение однородного,
— общее решение однородного,![]() — какое-либо частное решение неоднородного
ДУ.
— какое-либо частное решение неоднородного
ДУ.
Решение
однородного ДУ:
составляется характеристическое
уравнение
![]() ;
;
а)
корни
![]() — действительные,
— действительные,
![]()
![]() ;
;
б)
корни
— действительные,
![]()
![]() ;
;
в)
корни
![]() — комплексно сопряжённые
— комплексно сопряжённые
![]() .
.
Решение
линейного неоднородного ДУ
методом подбора:
если
![]() — многочлен от х степени m,
то
— многочлен от х степени m,
то
![]() ,
где
,
где
![]() — многочлен степени m
с неопределёнными коэффициентами,
— многочлен степени m
с неопределёнными коэффициентами,
![]() — кратность корня
— кратность корня
![]() характеристического уравнения.
характеристического уравнения.
8. Ряды
Ряд
![]() сходится, если
сходится, если
![]() где
где
![]() ;
;
![]() — сумма
ряда.
— сумма
ряда.
Ряд
сходится
![]() ;
;
![]() ряд
расходится.
ряд
расходится.
![]() .
.
![]() расходится.
расходится.
![]() .
.
Признаки сравнения положительных рядов:
1)
при
![]() :
:
а)
![]() ;
;
б)
![]() .
.
2)
![]()
![]() (эквивалентны).
(эквивалентны).
Признаки
сходимости положительных рядов
![]() :
:
1)
Даламбера:

2)
Радикальный
признак Коши:
Условия сходимости знакопеременных рядов:
![]() сходится
сходится
![]() сходится абсолютно;
сходится абсолютно;
сходится, а расходится сходится условно.
Признак
Лейбница
сходимости знакочередующегося
ряда
![]() ,
,
![]() :
если
:
если
![]() и
и
![]() ,
то ряд
сходится,
,
то ряд
сходится,
![]() .
.
Степенной
ряд
![]() :
интервал
сходимости
:
интервал
сходимости
![]() ,
,
радиус
сходимости
![]() или
или
![]() .
.
Степенные разложения:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Гармонические
колебания:
простая
гармоника
![]() или
или
![]() ,
где
,
где
![]() — амплитуда,
— амплитуда,
![]() — частота,
— частота,
![]() — начальная фаза.
— начальная фаза.
Ряд
Фурье
для функции
с периодом
![]() ,
заданной на
,
заданной на
![]() :
:
 ,
,
![]() ,
n=1,2,…
,
n=1,2,…
Ряд
Фурье
для функции
,
заданной на
![]() :
:
 а)
по
косинусам (
—
чётная функция,
а)
по
косинусам (
—
чётная функция,
![]() ):
):

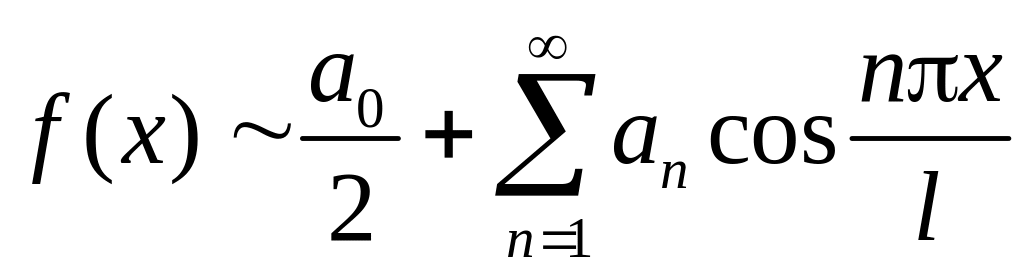 ;
;
![]() ;
;
 б)
по синусам
(
—
нечётная функция,
б)
по синусам
(
—
нечётная функция,
![]() ):
):
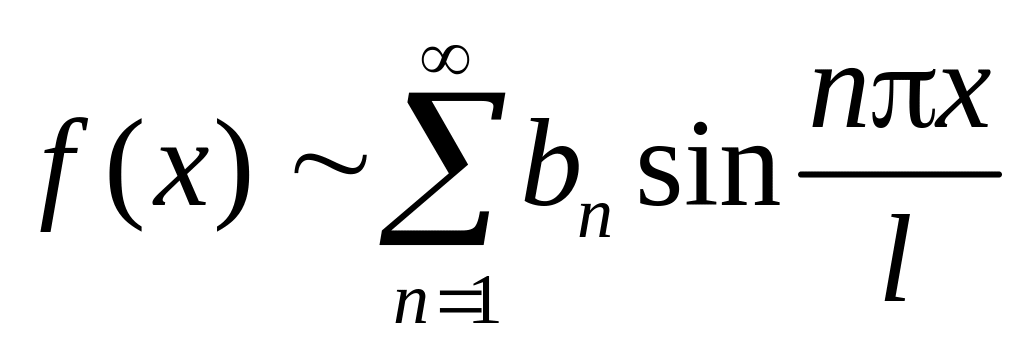 ;
;
![]() .
.
9. Теория вероятностей
Элементы комбинаторики:
Число
перестановок (упорядоченных
комбинаций)
из n
элементов:
![]() .
.
Число сочетаний (неупорядоченных комбинаций) из n элементов по m:
![]()
Число размещений (упорядоченных комбинаций) из n элементов по m:
![]() .
.
Сумма
событий
![]() — наступление хотя бы одного из событий
— наступление хотя бы одного из событий
![]() или
или
![]() .
.
Произведение
событий
![]() — наступление обоих событий
и
.
— наступление обоих событий
и
.
![]() ;
;
![]() — условная
вероятность события
при условии,
что событие
произошло в данном опыте.
— условная
вероятность события
при условии,
что событие
произошло в данном опыте.
Классическая
вероятность:
![]() ,
,
![]() — число всех случаев полной группы
попарно несовместимых,
равновозможных исходов опыта,
— число всех случаев полной группы
попарно несовместимых,
равновозможных исходов опыта,
![]() — число случаев,
благоприятствующих
событию А.
— число случаев,
благоприятствующих
событию А.
Геометрическая
вероятность:
![]() ,
,
![]() — мера (длина,
площадь или объём)
бесконечного множества
— мера (длина,
площадь или объём)
бесконечного множества
![]() всех элементарных исходов,
всех элементарных исходов,
![]() — мера подмножества всех элементарных
исходов из
,
благоприятствующих событию А. Используется
при равномерном распределении по
вероятностей событий,
прямо пропорциональных мере подмножеств
благоприятствующих исходов.
— мера подмножества всех элементарных
исходов из
,
благоприятствующих событию А. Используется
при равномерном распределении по
вероятностей событий,
прямо пропорциональных мере подмножеств
благоприятствующих исходов.
Теорема
сложения:
![]() .
.
Теорема
умножения:
![]() .
.
А
не зависит
от В (т.
е.
![]() )
)![]() .
.
Формула
Бернулли:
![]() ;
;
![]() ;
;
![]() ;
;
![]() — наивероятнейшее
(модальное)
значение числа появления события A
в серии из
независимых испытаний в схеме Бернулли,
— наивероятнейшее
(модальное)
значение числа появления события A
в серии из
независимых испытаний в схеме Бернулли,![]() — вероятность появления A
в каждом отдельном испытании.
— вероятность появления A
в каждом отдельном испытании.
Формула полной вероятности:
![]() ,
,
![]() — гипотезы
— гипотезы
(![]() — достоверно,
— достоверно,
![]() —
невозможно,
—
невозможно,
![]() ).
).
Функция распределения (интегральная) случайной величины (СВ) X:
![]() .
.
Функция
плотности вероятности:
![]() ;
;
![]() ;
;
![]() .
.
Математическое ожидание (среднее значение) СВ Х:
а)
Х — дискретная
СВ:
![]() ;
;
б)
Х —
непрерывная СВ:
![]() .
.
Дисперсия
СВ Х:
![]() ;
;
а)
Х — дискретная
СВ:
![]() ;
;
б) Х — непрерывная СВ:
![]() .
.
Среднеквадратическое
отклонение
СВ Х:
![]() .
.
Математическое
ожидание функции
![]() дискретной
СВ Х:
дискретной
СВ Х:
![]() .
.
Закон
Бернулли
(биномиальный):
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
![]() ;
;
![]() .
.
Закон
Пуассона:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Равномерный закон:


![]() ;
;
![]() .
.
Показательный
закон: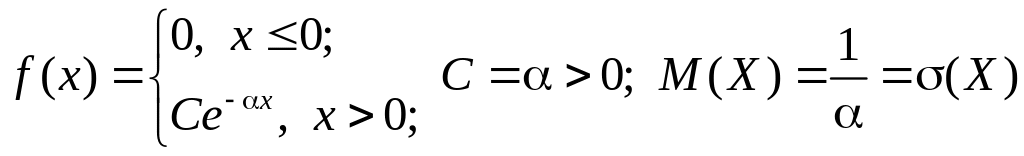 .
.
Нормальный
закон Гаусса: ;
;
![]() .
.
