Пример хэширования

Остановимся подробнее на алгоритме хэширования.

Пусть мы хотим найти хэш сообщения длиной b бит.

b - неотрицательное число (т.е. возможно 0), не обязательно кратное 8.

Примем за исходные данные сообщение:

«Одно из побочных применений хеширования состоит в том, что оно создает своего рода слепок, «отпечаток пальца» для сообщения, текстовой строки, области памяти и т. п. Такой «отпечаток пальца» может стремиться как к «уникальности», так и к «похожести» Яркий пример слепка — контрольная сумма.»

Длина строки сообщения больше 192 байт. Для получения битовой последовательности из сообщения используем ASCII – коды символов строки в двоичном представлении.

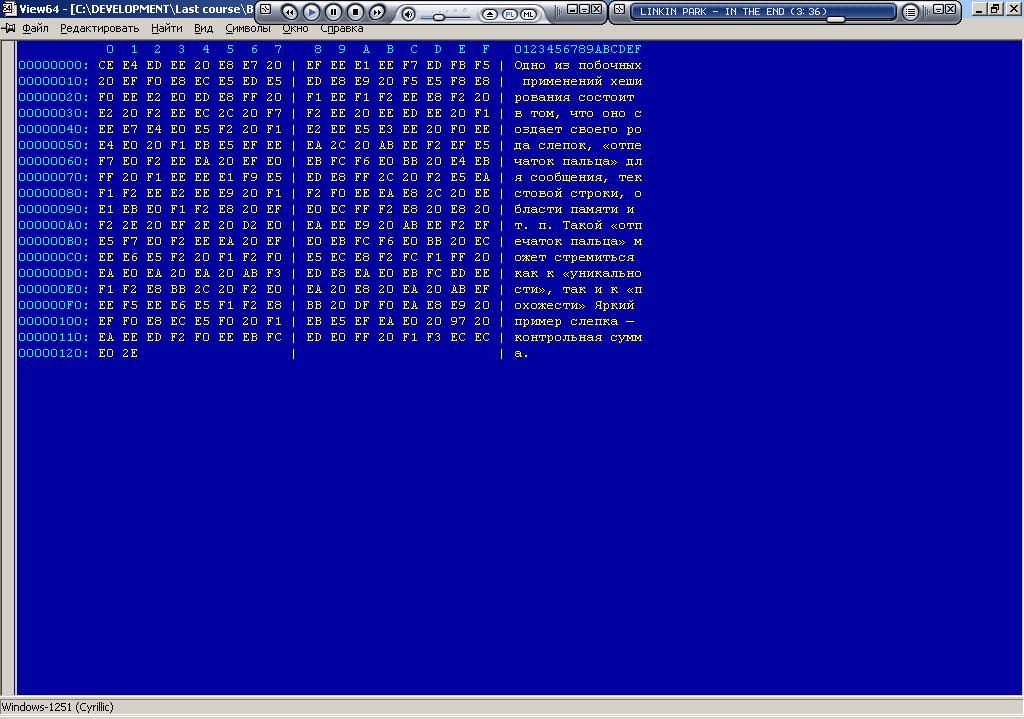
На рисунке использовано шестнадцатеричное представление символов сообщения.

12*16+2 = 194 байт = 1552 бита = (512 * 3 +16) бит.

Сообщение выравнивается до длины 448 по модулю 512. Выравнивание производится всегда, даже если длина сообщения и так равна 448. Выравнивание производится так: к сообщению добавляется один бит со значением <1>. Далее добавляются столько битов со значением <0>, сколько необходимо для того, чтобы длина стала равна 448. Вообще, добавляется минимум один, максимум 512 бит.

Таким образом, дополняем последний /четвертый/ блок до длины 448 бит:

16 бит + 1₂ + 431*0₂

Примечание: 16+1+431 = 448

Последний /четвертый/ блок, дополненный описанным выше способом будет выглядеть следующим образом:

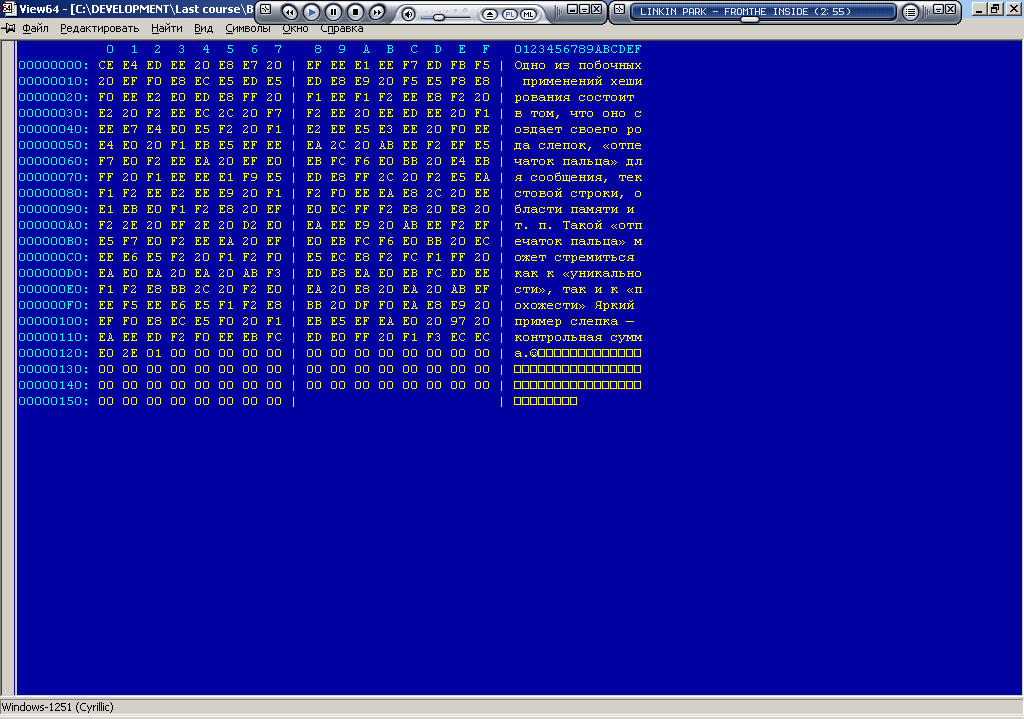
Далее к сообщению добавляется 64х-битовая длина оригинального сообщения. В маловероятном случае, если длина сообщения больше 2^64, добавляются только младшие 64 бита. Биты добавляются как два 32х битовых слова, младшее идет первым (всего 8 байт = 2слова по 4 байта).

Длина исходного сообщения 194байта = 1552 бита = 610₁₆ = 2¹⁰ +2⁹+2⁴.

11000010000₂

09876543210

610₁₆ = 2*16²+6*16¹+2*16⁰.

Записываем в первое 4 байтовое слово. Второе слово заполняем двоичными нулями.

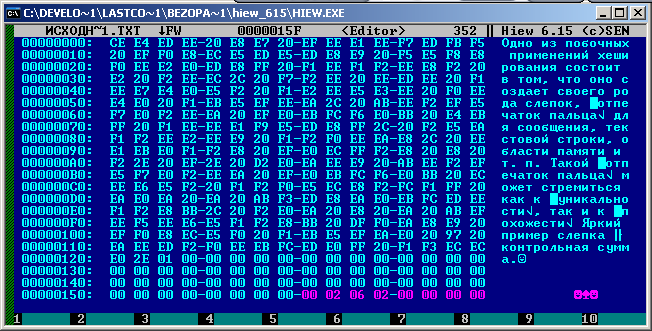
После этого шага сообщение имеет длину, кратную 512 битам. Разделим каждый его блок на 16 блоков длиной по 32 бита.

Получаем 4 * (16блоков*32бита) = 2048бит.

Алгоритм на каждом шаге хэширования получает на вход блок длиной 32 бита.

Приведенное выше описание дополнения сообщения до требуемой длины справедливо для большинства используемых сейчас алгоритмов хэширования, в частности для MD5.

Далее в действие вступает собственно алгоритм хэширования:

Для примера получения хэш-свертки можно рассмотреть самую элементарную функцию, при этом должно быть ясно, что криптостойкости подобная функция обеспечить не способна.

Описание:

Пусть на выходе мы должны получить хэш-свертку длиной 32 бита = 4 байта.

Пусть на вход функции получаем:

1. 32 -х битный блок данных /4 байта/;

2. 1 и 3 –й байты 32-х битного выхода алгоритма на предыдущем шаге.

Действия алгоритма:

1. Двоичное сложение 1 и 3, 2 и 4 байтов входного блока сообщения. При сложении перенос разряда не учитывается, т.е. берется младший байт результата каждого сложения.

2. Построение 4 байтового слова из полученных сумм и 1-го и 3-го байтов выхода с прошлого шага алгоритма: чередование как показано на рисунке.

3. Циклический сдвиг битов в слове влево на S бит, где S – сумма двоичных единиц в слове. Таким образом, если в слове 32 бита, то сдвиг может быть осуществлен на 0 – 32 бита влево.

4. Полученное в результате 4 байтное слово будет выходом алгоритма на каждом конкретном шаге.

На первом шаге алгоритма в качестве замены для байтов с предыдущего шага будем использовать значения следующего вида: 11001100₂ – замена первого байта выхода, 10101010₂ – замена третьего байта выхода.

На последнем шаге алгоритма на выходе получаем требуемое 32 битное значение хэш-свёртки нашего сообщения. При этом можно изменить байтовую последовательность выхода например с 1234 на 1432.

Для исходного текста, представленного в примере:

CE E4 ED EE – первый блок на входе

1: 11001110

2: 11100100

3: 11101101

4: 11101110

1+3: 110111011

|76543210 – разряды.

Оставляем последний байт: 10111011.

2+4: 111010010

|76543210 – разряды.

Оставляем последний байт: 11010010.

Т.к. мы находимся на первом шаге алгоритма, то в качестве дополнения берем

1доп: 11001100₂

2доп: 10101010₂.

10111011_11001100_11010010_10101010 - 32 – разрядное слово.

Подсчитываем количество единиц в слове: 18 единиц.

Осуществляем циклический сдвиг влево на 18 битов:

01001010101010101110111100110011

Разбиваем слово на байты:

01001010_10101010_11101111_00110011

1 2 3 4

Шаг не является последним, поэтому продолжаем выполнение алгоритма.

Выбираем в соответствии с алгоритмом 1 и 3 байты для использования на последующем шаге алгоритма:

1доп: 01001010₂

2доп: 11101111₂

Второй шаг алгоритма:

20 E8 E7 20 – следующие 4 байта в последовательности символов сообщения:

1: 00100000₂

2: 11101000₂

3: 11100111₂

4: 00100000₂

1+3: 100001000

|76543210 – разряды.

Оставляем последний байт: 1000₂

2+4: 100000111

|76543210 – разряды.

Оставляем последний байт: 111₂

Составляем 32 – разрядное слово:

00001000_01001010_00000111_11101111

Подсчитываем количество единиц в слове: 14 единиц.

Осуществляем циклический сдвиг влево на 14 битов:

10000001111110111100001000010010

Разбиваем слово на байты:

10000001_11111011_11000010_00010010 – хэш – свертка на шаге 2.

1 2 3 4

Шаг не последний, выбираем 1 и 3 байты для использования на последующем шаге алгоритма:

1доп: 10000001₂

2доп: 11000010₂

… последующие шаги выполняются аналогично. На последнем шаге при получении результирующей хэш-свертки изменим битовую последовательность выхода на: 1432.