Неполные д.У.Первого порядка

Определение. Д.У. первого порядка называется неполным, если функция явно зависит только от одной переменной: либо от , либо от .

1. .

2. . Методом разделения переменных определяется неизвестная функция (или ).

Уравнение называется автономным Д.У., такие уравнения имеют место в теории математического моделирования. Особый интерес представляют так называемые точки равновесия, или стационарные точки: нули функции , где .

Дифференциальные уравнения второго порядка.

Определение. Д.У. второго порядка называется уравнение вида

(1),

где х - независимая переменная, у – искомая функция, - соответственно первая и вторая производные.

Будем рассматривать уравнения, которые можно разрешить относительно второй производной:

(2).

Решением Д.У. второго порядка называется функция , определенная на некотором интервале , которая обращает это уравнение в тождество.

График решения называется интегральной кривой. Имеет место теорема Коши о существовании и единственности решения уравнения второго порядка.

Теорема Коши. Пусть функция и её частные производные непрерывны в некоторой области D пространства переменных . Тогда для любой внутренней точки этой области существует единственное решение уравнения (2), удовлетворяющее условиям:

. (3)

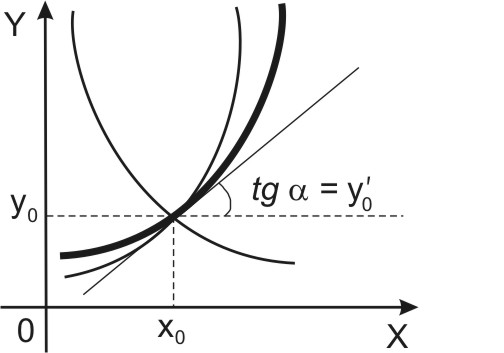
Геометрический смысл этой теоремы заключается в том, что через заданную точку ( ) на координатной плоскости проходит единственная интегральная кривая с заданным угловым коэффициентом касательной.

Условия (3) называются

начальными условиями,

а задачу отыскания решения

уравнения (2) с начальными

условиями (3) называют

задачей Коши.

Общим решением уравнения (2) в некоторой области D называется функция , если она является решением этого уравнения при любых постоянных величинах , которые могут быть определены единственным образом при заданных начальных условиях (3).

Ч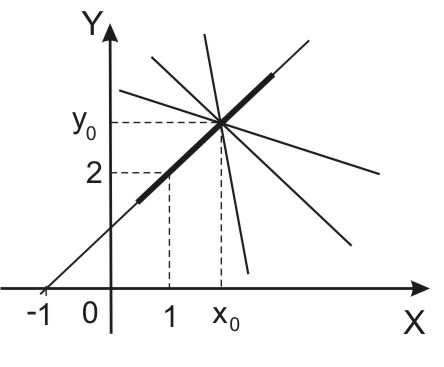 астным решением уравнения (2) называется общее решение этого уравнения при фиксированных значениях постоянных : .

Пример. .

Дважды интегрируя, найдем общее решение:

, где произвольные постоянные.

Это решение представляет собой семейство прямых,

проходящих в произвольных направлениях,

причем через каждую точку плоскости

проходит бесконечное число таких прямых.

Поэтому для выделения частного решения,

проходящего через заданную точку ( ), следует

задать ещё и угловой коэффициент прямой,

совпадающий в данном случае со своей касательной.

Например, найдем частное решение, удовлетворяющее

начальным условиям

,

т.е. найти прямую, проходящую через точку (1,2), с угловым коэффициентом, равным 1.

Т.к. решение представлено как , подставим в него начальные условия, получим

.

На чертеже - это жирная прямая.

Дифференциальные уравнения второго порядка, допускающие понижение порядка.

1).

Такое уравнение решается последовательным интегрированием.

Пример. . , = .

2). .

Вводится вспомогательная функция: . .

Получим линейное уравнение первого порядка относительно и z : .

Найдем , перейдем к , затем получим .

Пример. .

Введем . .

Получим линейное уравнение первого порядка относительно : .

Решим его методом подстановки.

, . (*)

, положим .

Найдем частное решение этого уравнения: , ln , .

Подставим это решение в уравнение (*).

Получим или .

, .

.

. .

.

3). . Нет переменной .

Полагаем . Тогда = , т.е. .

Подставим в исходное уравнение, получим = .

Получим уравнение первого порядка относительно ,

решение такого уравнения или .

Тогда , .

Пример. .

Положим , тогда .

. .

Решаем методом разделения переменных: . ( .

, где у > 0. , ,

, или .

При делении на z было «потеряно» решение уравнения , т.е.