66. Точность обсервации при определении места судна по разновременным измерениям высот светил…

Положение ВЛП2, так же как и положение ВЛП1 ( до привидения ее к одному месту) не зависит от погрешности в счислимых координатах. Однако счислимо-обсервованное место судна будет содержать дополнительную погрешность, если учитываемый вектор плавания судна за время между наблюдениями не соответствует действительному.

Именно по этой причине место судна, полученное по разновременным наблюдениям Солнца называется не обсервованным, а счислимо-обсервованным.

Погрешность в счислении растет пропорционально продолжительности плавания. Погрешность счислимо-обсервованного места складывается из совместного влияния погрешности счисления в промежутке между первыми и вторыми наблюдениями и погрешностей в ВЛП1 и ВЛП2.

Радиальная (круговая) СКП счислимо-обсервованного места судна рассчитывается по формуле:

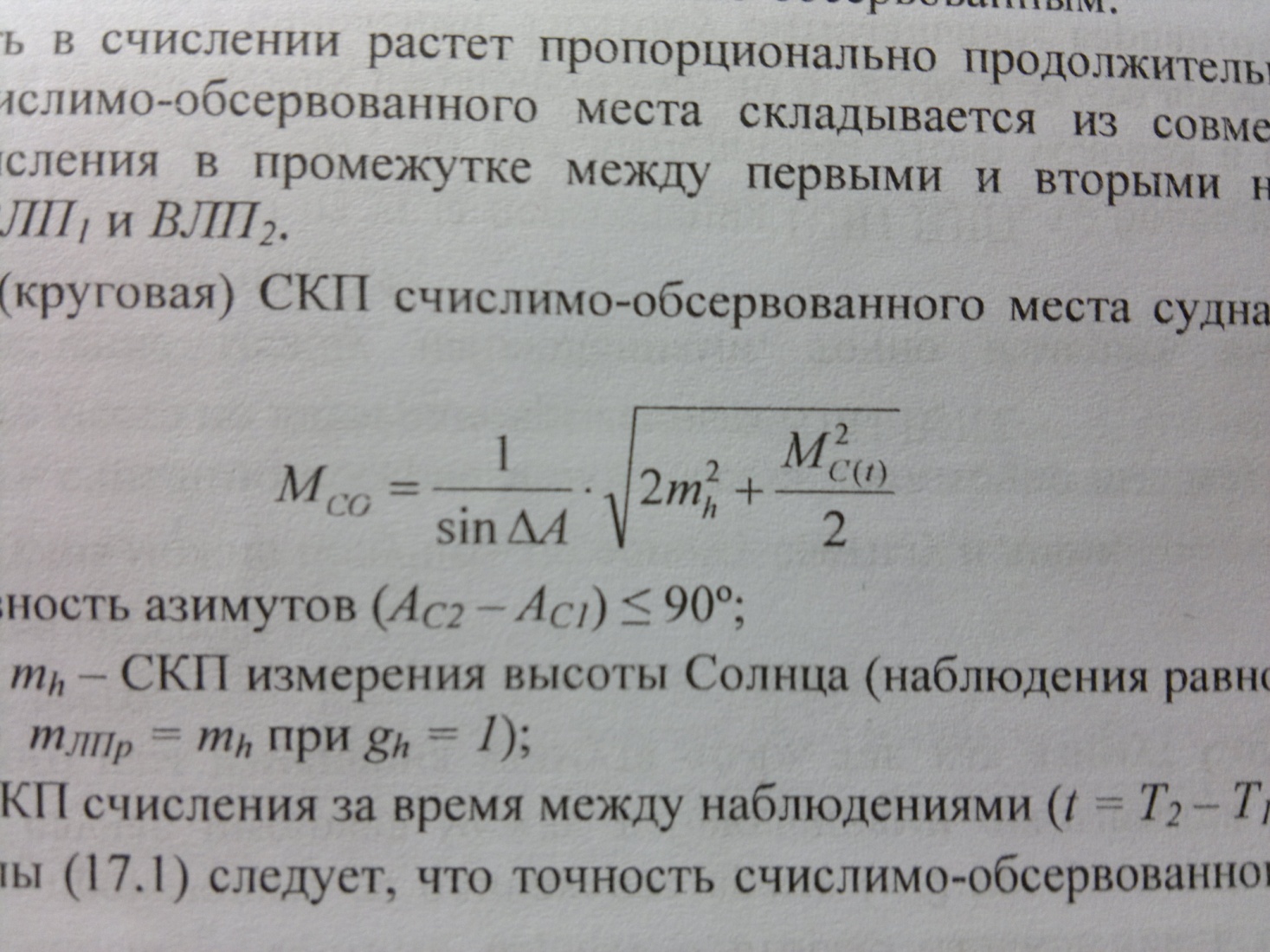
Где ΔА – разность азимутов (Ас2-Ас1)≤90°;

Mh- СКП измерения высоты Солнца (наблюдения равноточны, т.е. mЛП1=mЛП2=mЛПр=mh при gh=1);

Mc(t) – СКП счисления за время между наблюдениями (t=T2-T1).

Из формулы (17.1) следует, что точность счислимо-обсервованного места зависит от:

- точности измерения высоты – mh;

- угла пересечения ВЛП ВЛП - ΔА =Ѳ=Ас2-Ас1;

- точности счисления пути судна за время между наблюдениями

Mc(t)=Kc* , (мили)

Где t=T2-T1 (час.)

Кс- коэффициент точности счисления пути судна.

Для повышения точности способа необходимо особо тщательно вести графическое счисление между наблюдениями, точно измерять высоты Солнца и добиваться большего значения ΔА.

Если исходить только из угла пересечения ВЛП ВЛП, то более высокую точность мы получим при –

ΔА =Ѳ=90°, но для выполнения этого условия в средних широтах необходимо иметь время между наблюдениями до 6 часов, а за это время преобладающей уже будет погрешность в счислении. Поэтому оптимальным вариантом можно считать изменение азимута Солнца на 40-50°

67. Частные случаи исправления высот светил…

Частный случай исправления высот светил

К частным случаям относятся измерения высот любого светила, выполненные необычным приемом или не над

видимым горизонтом, в связи с чем порядок исправления высот изменяется.

Исправление высот светил, измеренных «через зенит». Этот прием измерения высот, возможный при высо-тах, больших 45—50°, за

последнее время при-обретает распростра-нение и применяется при

измерении не толь-ковысот Солнца, но и высот других светил (он дает

возможность вы-явить ошибки и промахи).

Исправление висот Солнца, измеренных «через зенит».

Рекомендуется измерять высоту, «погружая в море» изображение

Солнца, т. е. касаясь горизонта краем н' (рис. 3.17), который при обычном

измерении является нижним (н). Исправлять высоту можно с любыми

таблицами. По полученному ос выбирают s и получают h H' = ос

Z

+i+s-d т. е. высота Рис. 3.17

приводится к истин горизонту. Эту h H' надо вычесть из

Z

1800

и получить h H , которая и исправляется в обычном порядке (раздельными

B

или общими поправками). Формула для исправления имеет вид:

h = [180° – (oc + i + s – d)] + ( – po + p) ± R

При этих высотах поправки Δht,B, обычно меньше 0,1', и ими пренебрегают.