
- •1.Предмет теории вероятностей.
- •2.Какие бывают события? Дайте определение каждому из них.
- •3.Что такое случайное событие? Какие виды случайных событий вы знаете? Раскройте сущность каждого вида.
- •4.Что представляет собой полная группа событий? Дайте пример.
- •5.Раскройте сущность основных формул комбинаторики.
- •6.Что такое элементарный исход? Приведите классическое определение вероятности.
- •7. Что такое частота или статическая вероятность случайного события?
- •8. Напишите теоремы сложения вероятностей.
- •9. Приведите теоремы умножения вероятностей.
- •10. Что такое формула полной вероятности?
- •11. Приведите формулу Байеса и объясните ее суть.
- •12. В чем заключается формула Бернулли?
- •13. Приведите формулу Пуассона и укажите, когда она применима?
- •14. Приведите формулы Муавра-Лапласа и укажите, когда их применяют?
- •15. Раскройте сущность понятия «Случайная величина»? приведите пример.
- •16. Что такое функция распределения? Укажите ее свойства.
- •17. Дайте определение понятиям: «Дискретно распределенная случайная величина» и «Непрерывно распределенная случайная величина».
- •18.Приведите законы распределения дискретных случайных величин.
- •19. Приведите законы распределения непрерывных случайных величин.
- •20. Что такое математическое ожидание, дисперсия случайной величины?
- •21. Что представляет собой правило трех сигм?
- •22.Дайте определение генеральной совокупность, выборке.
- •24. Что представляет собой эмпирическая функция распределения?
- •26.Что такое точечное оценивание? Приведите свойства точечных оценок, оценки
- •27.Раскройте метод наибольшего правдоподобия и метод моментов нахождения оценок параметров распределений.
- •30.Дайте определение статистической гипотезы, критерия, ошибок первого и второго рода.
- •31.Дайте определение критической области, мощности критерия.
- •32. Приведите схему проверки статистической гипотезы.
- •33. Что представляет собой проверка гипотез о математическом ожидании и дисперсии случайной величины, распределенной по нормальному закону?
- •35. Что такое проверка гипотез о равенстве математических ожиданий и дисперсий?
- •36. Раскройте сущность однофакторного и двухфакторного дисперсионного анализа.
- •39. Объясните понятие стохастической корреляционной зависимости, регрессии. Что представляют собой задачи корреляционного и регрессионного анализа.
- •40. Как производится построение эмпирического уравнения прямой регрессии?
- •44. Что такое множественная линейная регрессия и корреляция?
18.Приведите законы распределения дискретных случайных величин.
Законом
распределения дискретной случайной
величины называют соответствие между
возможными значениями случайной
величины и вероятностями их появления.
Его можно задать таблично, аналитически
(в виде формулы) или графически (в виде
многоугольника распределения). Рассмотрим
случайную величину X, которая принимает
значения x1, x2, x3 ... xn с некоторой
вероятностью pi, где i = 1.. n. Сумма
вероятностей pi равна 1.
![]() Таблица
соответствия значений случайной
величины и их вероятностей вида
Таблица
соответствия значений случайной
величины и их вероятностей вида
Таблица
соответствия значений случайной
величины и их вероятностей вида
Таблица
соответствия значений случайной
величины и их вероятностей вида
x1 |
x2 |
x3 |
... |
xn |
... |
p1 |
p2 |
p3 |
|
pn |
|
называется рядом распределения дискретной случайной величины или просто рядом распределения. Эта таблица является наиболее удобной формой задания дискретной случайной величины.
19. Приведите законы распределения непрерывных случайных величин.
Для описания закона распределения непрерывной случайной величины Х предлагается другой подход: рассматривать не вероятности событий Х=х для разных х, а вероятности события Х<х. При этом вероятность P(X<x) зависит от текущей переменной, т. е. является некоторой функцией от х.
Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х:
![]() .
Функцию F(x) называют интегральной
функцией распределения или интегральным
законом распределения. Равномерный
закон распределения. Непрерывная
случайная величину Х имеет равномерный
закон распределения (закон постоянной
плотности) на отрезке [a; b], если на этом
отрезке функция плотности вероятности
случайной величины постоянна, т.е. f(x)
имеет вид:
.
Функцию F(x) называют интегральной
функцией распределения или интегральным
законом распределения. Равномерный
закон распределения. Непрерывная
случайная величину Х имеет равномерный
закон распределения (закон постоянной
плотности) на отрезке [a; b], если на этом
отрезке функция плотности вероятности
случайной величины постоянна, т.е. f(x)
имеет вид:
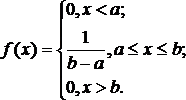 Нормальный
закон распределения (закон Гаусса).
Непрерывная случайная величина Х имеет
нормальный закон распределения с
параметрами и (обозначают ), если ее
плотность вероятности имеет вид:
Нормальный
закон распределения (закон Гаусса).
Непрерывная случайная величина Х имеет
нормальный закон распределения с
параметрами и (обозначают ), если ее
плотность вероятности имеет вид:
![]() где
где
![]() ,
,
![]()
20. Что такое математическое ожидание, дисперсия случайной величины?
Математическое
ожидание M дискретной случайной величины
- это среднее значение случайной
величины, равное сумме произведений
всех возможных значений случайной
величины на их вероятности.
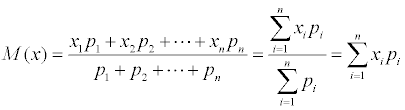
Дисперсия
случайной величины — мера разброса
случайной величины, равная математическому
ожиданию квадрата отклонения случайной
величины от ее математического ожидания.
![]()
21. Что представляет собой правило трех сигм?
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм. Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D: Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю. Это правило называется правилом трех сигм. Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
