2.3. Погрешности измерений.

При практическом использовании тех или иных измерений важно оценить их точность. Термин "точность измерений", т. е. степень при­ближения результатов измерения к некоторому действительному зна­чению, не имеет строгого определения и используется для качествен­ного сравнения измерительных операций; Для количественной оцен­ки используется понятие "погрешность измерений" (чем меньше погрешность, тем выше точность). Оценка погрешности измерений — одно из важных мероприятий по обеспечению единства измерений.

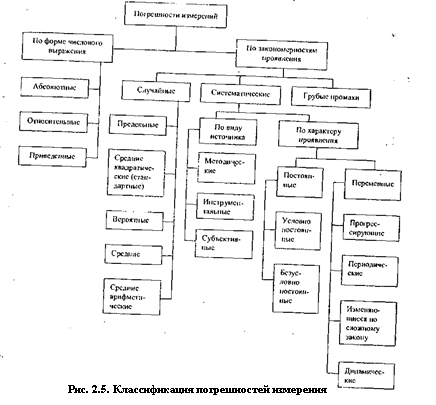
Количество факторов, влияющих на точность измерения, дос­таточно велико, и любая классификация погрешностей измере­ния (рис. 2.5) в известной мере условна, так как различные по­грешности в зависимости от условий измерительного процесса проявляются в различных группах.

2.4. Нормирование погрешностей и формы представления результатов измерений.

Основные задачи нормирования погрешностей заключаются в выборе показателей, характеризующих погрешность, и установлений допускаемых значений этих показателей. Решение этих за­дач определяется целью измерений и использованием результатов. Например, если результат измерения используется наряду с дру­гими при расчете какой-то экспериментальной характеристики, то необходимо учитывать погрешности отдельных составляющих путем суммирования их СКО.

Если речь идет о контроле в пределах допуска и нет информа­ции о законах распределения параметра и погрешности, то доста­точно ограничиться доверительным интервалом с доверительной вероятностью. Эти показатели должны сопровождать результаты измерений тогда, когда дальнейшая обработка результатов не пре­дусмотрена.

Исходя из изложенного, для оценки погрешностей измерений необходимо: установить вид модели погрешности с ее характер­ными свойствами; определить характеристики этой модели; оце­нить показатели точности измерений по характеристикам модели.

При установлении модели погрешности возникают типовые статистические задачи: оценка параметров закона распределения, проверка гипотез, планирование эксперимента и др.

В соответствии с МИ 1317—86 точность измерения должна вы­ражаться одним из способов:

1) интервалом, в котором с установленной вероятностью на­ходится суммарная погрешность измерения;

2. интервалом, в котором с установленной вероятностью на­ходится систематическая составляющая погрешности измерений;

3. стандартной аппроксимацией функции распределения случайной составляющей погрешности измерения и средним квадратическим отклонением случайной составляющей погрешности из­мерения;

4. стандартными аппроксимациями функций распределения систематической и случайной составляющих погрешности изме­рения и их средними квадратическими отклонениями и функци­ями распределения систематической и случайной составляющих по­грешности измерения.

При отсутствии данных о виде функций распределения со­ставляющих погрешности результата и необходимости дальней­шей обработки результатов или анализа погрешностей результаты измерений представляют в форме а, о, и, Д_с. Если вычислены гра­ницы не исключенной систематической погрешности, то следует дополнительно указать доверительную вероятность.