13. Криволінійний інтеграл.

Якщо обл.. інтегр. є не сегмент, а деяка крива, то інт. наз. криволінійним. Розглянемо інт. заданий вздовж кривої АВ. Розіб’ємо АВ т. на n довіл. частин. На кожній дузі , виберемо довіл. чином т. , . Складемо , де - це довжина дуги , а - деяка непер. ф-ія визнач. на АВ. Таку суму наз. інтеграл. сумою ф-ії на АВ. Нехай - набіл. Знач. довжин дуг . Якщо інт. сума при має скінч. границю, яка не залежить від способу розбиття та від вибору т. , то цю границю наз. кривол. інт. 1-го роду (або кринол. інт. по довжині дуги) від ф-ії по кр. АВ і познач. , де L – довжина всієї дуги АВ.

Властивості: 1) ; 2) ; 3)Якщо т.С лежить на АВ, то: . Обчислення: Нехай АВ задана парам.: , і ці ф-ії непер-ні разом зі своїми похідними, тоді d = , . Якщо кр. задана не парам., а рів-ям , то: . Застосування: Площа циліндричної поверхні, що визнач. ф-ією : . Довжина дуги АВ: . Фіз. зміст: маса кривої: з густиною .

, де  - проекція вектора на вісь ОХ, а наз. кривол. інт. 2-го роду по корд-ті х. Якщо існують два інт. та , то суму наз. кривол. інт. 2 роду (або кривол. інт. по координатах) і познач. . Фіз. зміст: робота змінної сили по переміщенню матеріальної т. вздовж кр. ВС: , де - це проекції сили F на координатні осі ОХ та ОУ.

Властивості: 1) Сталий множник можна виносити за знак інт.; 2) кривол. інт. від суми скінч. к-сті ф-ій дорівнює відповідній сумі кривол. інт. 3)Якщо т. С належить кривій АВ, то ; 4) .

Обчислення: Якщо АВ задана парам. , , то . Якщо явно і : .

Якщо інт. записаний по додатньому замкненому контурі (проти годинникової стрілки), то познач. .

Якщо задано правильну обл.., яка обмежена лініями , то її площа шукається за ф-лами: , , ,

Формула Гріна: .

14. Тригонометричний ряд Фур’є.

Ряд виду (1) наз. тригонометричним рядом Фур’є, а числа - його коефіцієнтами. Припустимо, що р. (1) рівномірно збіг-ся на до ф-ії , тобто (2). Оскільки вказаний р. рівномірно збіг-ся на і його члени неперервні на всій числовій прямій, а значить і на , то його можна почленно інтегрувати на вказаному сегменті. Це твердження зберігає силу, якщо р. (2) помножити на будь яку інтегровну ф-ію на . Ці обставини разом з ортогональністю системи тригонометричних ф-ій дозволяють знайти коефіцієнти. Проінтегруємо р. 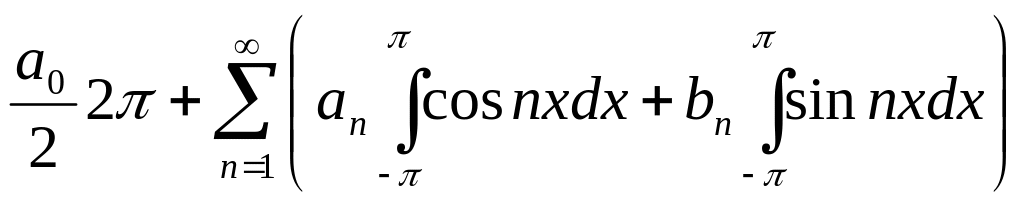(2) почленно: (3)

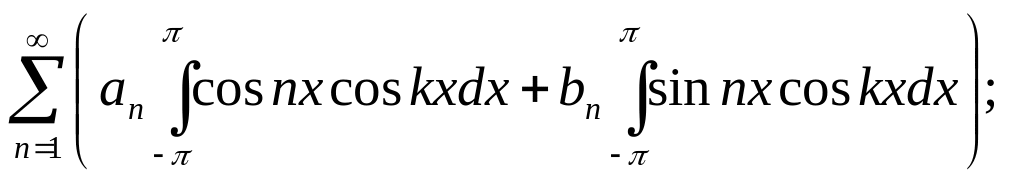
Домноживши ліву і праву частину (2) на і проінтег-ши: ; (4). Аналогічно помноживши (2) на і проінтегр-ши, дістанемо: (5).

Тригон. ряд (1), коефіцієнти якого визнач-ся за ф-лами (3)-(5) наз. рядом Фур’є для -періодичної ф-ії , а його коефіцієнти – коефіцієнтами Фур’є.

Для існування інтегралів (3)-(5) достатньо інтегровності самої ф-ії на . Якщо ф-ія є парною, то вона розкладається в ряд Фур’є по . Якщо є непарною, то по .

Т. Якщо ф-ію можна подати на у вигляді деякого рівномірно збіжного тригонометричного ряду, то цей ряд єдиний і він є рядом Фур’є даної ф-ії.

Т. (дост. умова збіжності р. Фур’є) Нехай ф-ія є -періодич-ю, кусково-монот-ю і обмеженою на . Тоді ряд Фур’є цієї ф-ії є збіжним на всій числовій прямій, причому сума цього ряду рівна значенню ф-ії в усіх точках неперервності.

Якщо ф-ія на розклад-ся в ряд Фур’є і вона парна, то ряд має вигляд: , а якщо непарна, то:

Комплексна форма ряду Фурє має вигляд: , де або де .

Пр. Розкласти в ряд Фур’є ф-ію на інтервалі

Періодично продовжимо дану ф-ію. Оскільки ф-ія парна, то: ;

.

1. Збіжні числові послідовності. Знайти

2.Ознаки збіжності числ. рядів. Дослідити на збіжність.

3.Границя функції в точці, властивості. Знайти

4.Неперервність функції, властивості. Дослідити на неперервність

5.Похідна, правила диференціювання. Знайти , якщо

6.Диференційовність функції кількох змінних. Знайти , якщо

7.Застосування похідної до дослідження ф-ії. Знайти екстремуми ф-ії

8.Екстремуми ф-ій багатьох змінних. Дослідити на екстремум

9.Невизначений інтеграл, властивості. Знайти .

10.Визначений інтеграл, формула Ньютона-Лейбніца. Обчислити:

11.Застос-я визначеного інтеграла. Обчислити об’єм тіла, утвореного обертанням фігури навколо осі ОХ.

12.Розклад функції у степеневий ряд. Розкласти за степенями х функцію .

13.Криволінійний інтеграл. Обчислити

14.Тригонометричний ряд Фур’є. Розкласти в ряд Фур’є функцію на інтервалі