9. Невизначений інтеграл, властивості. Знайти .

Ф-ія F(х) наз. первісною до ф-ії f(х) на [a;b], якщо : .

Т. Якщо ф-ія F(х) є первісною до ф-ї f(х) на [a;b], то довільну іншу первісну до цієї ф-ії можна подати у вигляді: , де с=const.

Сукупність всіх первісних до ф-ї f(х) на [a;b] наз. невизначеним інтегралом і познач. . =

Властивості невизначеного інтегралу: ; ; ; .

Таблиця інтегралів: ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; .

Основні методи інтегрування: 1. Метод підстановки (метод заміни змінної): Нехай ф-ія F(t) є первісною до ф-ії на мнж. Т і на мнж. Х задано ф-ію з мнж. значень Т, тобто ф-ію . Ф-ія є дифер-на на мнж. Х. Тоді на мнж. Х будуть визначені ф-ії , причому , або що те саме . Остання рівність означає, що ф-ія є первісною до ф-ії на мнж. Х. Тому . 2.Інтегрування частинами:

Інтегрування раціональних функцій: всі найпростіші дроби поділяються на чотири види:1) ; 2) ; 3) ; 4) .

1) ; 2) ; 3) .

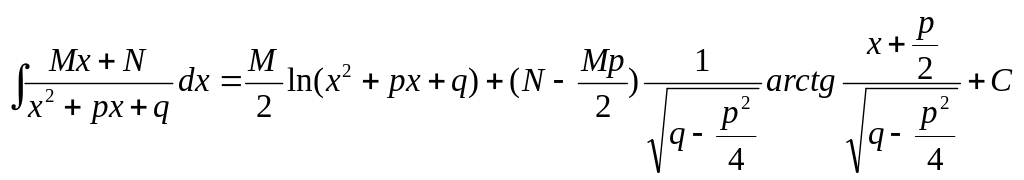Інтегрування тригонометричних ф-ій: , де - раціональна ф-ія береться за допомогою універсальної підстановки: . ; .

Інтегрування біноміальних диференціалів: . Виділяють три випадки: 1) - ціле, тоді викор. заміну , де s- спільний знаменник дробів m та n. 2) - ціле, тоді викор. підстановку , де s- знаменник дробу p. 3) - ціле, тоді викор. заміну , де s- знаменник дробу p.

10. Визначений інтеграл, формула Ньютона-Лейбніца. Обчислити:

Нехай на задано ф-ію . Розіб’ємо на n довільних частин точками. . Позначимо таке розбиття буквою Т і нехай На кожній з отриманих частин виберемо довільним чином т. і обчислимо . При кожному обчислимо добутки . Складемо суму , яку наз. інтегральною або ріманованою сумою ф-ї на .

Скінченна границя (якщо вона існує) інтегральних сум при , наз. визначеним інтегралом ф-ії на сегменті і познач. .

Т. (Необх. умова інтегровності) Якщо ф-ія інтегровна на сегменті, то вона на цьому сегменті обмежена.

Т. (НіД умова інтегровності ф-ії) Для того, щоб ф-ія була інтегровною на сегменті НіД, щоб . Тут S_Т, s_Т – верхня і нижня суми Дарбу: , , , , .

Достатні умови інтегрованості ф-ій:

Т. Якщо ф-ія неперервна на , то вона на цьому сегменті інтегровна.

Т. Якщо ф-ія обмежена на і має на цьому сегменті скінчену к-сть точок розриву, то вона на цьому сегменті інтегровна.

Т. Якщо ф-ія монотонна на , то вона на цьому сегменті інтегровна.

Властивості визначеного інтегралу: 1) ; 2) ; 3) Якщо ф-ія - інтегровна на , а с-довільне число, то -також інтегровна на , при чому ; 4) Якщо ф-ії інтегровні на , то інтегровними на цьому сегменті будуть ф-ії , причому ; 5) Якщо ф-ія інтегровна на , то ф-ія буде інтегровною і на сегментах і , причому ; 6) Якщо : , то ; 7) : , то ; 8)

Т. (про середнє) Якщо ф-ія неперервна на сегменті , то на цьому сегменті т. с, що

Т. (ф-ла Ньютона-Лейбніца) Якщо ф-ія неперервна на і F(x) – деяка її первісна на цьому сегметі, то має місце ф-ла: .