1. Збіжні числові послідовності.

Якщо кожному натур. числу n ставиться у відповідність дійсне число а_n то кажуть, що на мнж. натур. чисел задана послід. дійсних чисел і познач. , де x₁, x₂,…- члени послід., а x_n – загал. член послід. Або послід. – це ф-ія, яка задана на мнж. натур. чисел і набуває значень з мнж. дійсних чисел. Послід. можна задати різними способами: переліком елементів (1,1/2, 1/3,...); ф-лою загал. члена ( ); рекурентним співвідношенням ( ). Число а наз. границею послід. , якщо . Якщо послід. має границю ( ), то вона збіжна, інакше – розбіжна. Напр.: - послід. збіжна має границю 0, - розбіжна. Інтервал наз. -околом числа а. Геометр. зміст границі послід.: Якщо число а є границею послід. , то в довільному як завгодно малому -околі т. а містяться всі члени послід. починаючи з деякого номера n₀. При цьому в -околі буде безліч членів послід., а поза ним скінченна к-сть (не більше ніж n₀ штук).

Властивості збіжних послід.: Т. (про єдиність границі) Кожна збіжна послід. має єдину границю. Або якщо послід. збіжна, то вона має єдину границю.

Т. (про обмеженість збіжної послід.) Якщо послід. збіжна, то вона обмежена.

Т. (про нерівність між членами послід-тей) Якщо дві послід-ті (x_n), (y_n) збіжні і , , причому a<b, то починаючи з деякого номера буде виконуватись нерівність x_n< y_n.

Т. (про перехід до границь в нерівностях) Якщо , , і починаючи з деякого номера і x_n≥ y_n, то a b.

Т.(про границю проміжної послід.) Нехай задано три послід-ті (x_n), (y_n), (z_n), для яких: x_n y_n z_n, ; , тоді .

Послід. наз. нескінченно малою, якщо її границя рівна нулю або .

Т. (про структуру збіжної послід.) Для того щоб послід. була збіжною і мала границею число a НІД, щоб її загал. член можна було подати у вигляді , де - нескінченно мала.

Т. Алгебраїчна сума двох нескінченно малих послід. є нескінченно малою.

Т. Добуток нескінч. малої послід. на обмежену є нескінч. малою.

Послід. наз. нескінч-о. великою послід., якщо . Той факт, що послід. нескінч-о велика записують:

Т. Якщо послід. є нескінч-о великою, то є нескінч-о малою.

Послід. наз. зростаючою (спадною), якщо : ( ). Послід. наз. неспадною (незростаючою), якщо ( ).

Т. Нехай послід. неспадна, тоді: якщо вона обмежена зверху, то вона збіжна і границею її є точна верхня межа ; якщо вона не обмежена зверху, то вона є додатною нескінч-о великою: .

Т. (критерій Коші збіжності послід.) Для того щоб послід. (x_n) була збіжною НіД, щоб для вона була фундаментальною: .

Пр.

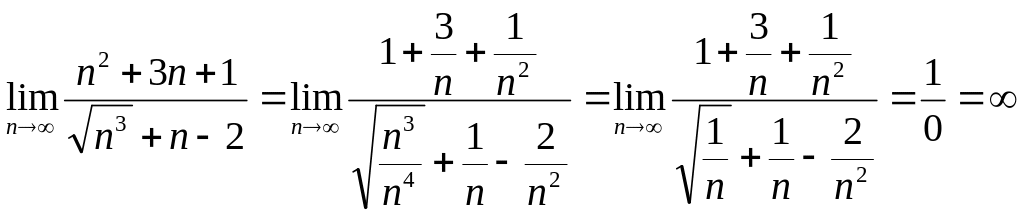
2. Ознаки збіжності числових рядів.

Нехай задана послід. дійсних чисел Тоді вираз виду (1) наз. числ. рядом. Числа наз. членами ряду, - загал. членом ряду. Часто ряд виду (1) записують . Запишемо для ряду (1) суми: . Такі суми наз. частинними сумами ряду (1). При цьому можна розглядати послід. частинних сум . Якщо послід. част. сум ряду (1) є збіжною, то ряд наз. збіжним. При цьому границя послід-ті част. сум наз. сумою ряду. Тобто

Т. (крит. збіжності числ. ряду) Щоб ряд (1) збігався НіД, щоб або

Т. (необх. умова збіжності ряду) Якщо ряд (1) збіжний, то його загал. член прямує до нуля, тобто

Ознаки збіжності знакододатніх рядів: Нехай для ряду (1) викон-ся умова . Такий ряд наз. рядом з додатними членами або знакододатнім. Т. Щоб знакодод. ряд був збіжним НІД, щоб послід. його част. сум була обмежена зверху.

Т. (ознака порівняння збіжності числ. ряду) Нехай задано два знакодод. ряди (1) і (2),причому починаючи з деякого номера , тоді із збіжності ряду (2) випливає збіжність ряду (1), а із збіжності ряду (1) - розбіжність ряду (2).

Т. (гранична ознака порівняння) Нехай для знакодод. рядів (1) і (2) існує скінч. відмінна від нуля границя . Тоді (1) і (2) збігаються чи розбігаються одночасно.

Т. (ознака Даламбера) Нехай для знакодод. ряду (1) існує границя . Тоді: при q<1 ряд збіж., при q>1- розбіж.; при q=1 сумнівний випадок.

Т. (ознака Коші) Нехай для знакодод. ряду (1) існує границя . Тоді: при q<1 ряд збіж., при q>1 – розбіж.; при q=1 сумнівний випадок.

Т. (інтегральна ознака Коші-Маклорена) Нехай для знакодод. ряду (1) викон. 1) ; 2) . І на пром.. визначена непер. монотонно спадна ф-ія f(x), для якої . Тоді цей ряд збіг-ся або розб-ся разом з невласним інт. .

Ознаки збіжності знаком. рядів: Ряд, члени якого змінюють почергово свій знак наз. знаком.. Такий ряд записують так: , де . Т. (ознака Лейбніца збіжності знаком. ряду) Якщо в знаком. ряді ( ) (1) буде: ; , то ряд збіж., а сума ряду додатна і не перевищує 1-го члена .

Ознаки збіж. рядів довіл. знаків: Нехай задано ряд (1), серед членів якого є як додатні, так і від’ємні. Такі ряди наз. рядам з членами довіл. знаків. Ряд виду (1) наз. абсол. збіжним, якщо збіжним є ряд складений з його модулів. Т. Якщо ряд з довіл. членами (1) є абсол. збіжним, то він є збіжним.

Якщо ряд (1) збіг., а ряд складений з його модулів розбіг., то ряд (1) наз. умовно збіжним. Т. (асоціат. збіжного ряду) Нехай числ. ряд (1) абсолютно збіг. і його сума S. Тоді ряд (2) утворений з ряду (1) об’єднанням членів групи без перестановок також збіж. і його сума S. Т. (Коші) Якщо ряд (1) є абсол. збіж. і його сума S, то ряд утворений з нього довільною перестановкою членів ряду є також абсол. збіжний з сумою S. Т. (Рімана) Якщо ряд (1) умовно збіжний, то яке б не було число L (навіть ) члени ряду (1) можна переставити так, щоб одержаний ряд мав суму рівну L.

Пр. Дослідити на збіжність . За ознакою Даламбера: 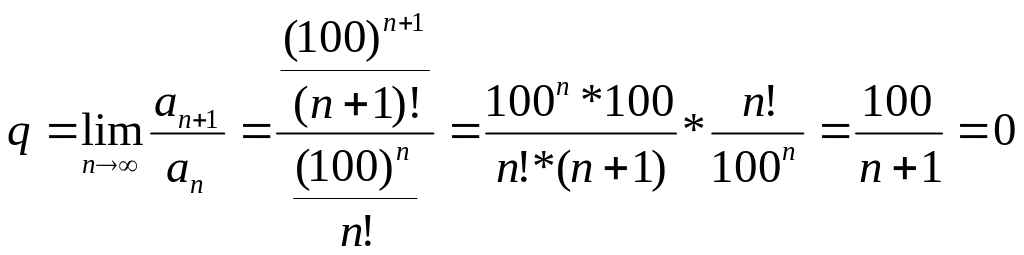- ряд розбіжний.