8.Потенциал.Потенциал точечного заряда, система точечных зарядов.

Потенциал поля точечного заряда Q в однородной изотропной среде с диэлектрической проницаемостью e :

Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Qi (i = 1, 2, ... , n). Энергия взаимодействия всех n зарядов определится соотношением

где rij - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.

9.Потенциал диполя

Электростатическое поле обладает двумя характеристиками: силовой –

напряженностью электрического поля Е и энергетической – потенциалом φ.

Напряженность электрического поля численно равна силе, действующей на положительный точечный заряд и отнесенной к величине этого заряда:

Е=F/q;

потенциал численно равен потенциальной энергии заряда Еп в электростатическом поле, отнесенной к величине этого заряда:

φ=Еп/q

Согласно закону Кулона для точечного заряда, находящегося в вакууме

Е=kq/r2

φ=kq/r.

Здесь k = 9•109 Н•м2/Кл2, q – величина заряда, r- расстояние от заряда до точки, где определяется напряженность электрического поля или потенциал.

Если электрическое поле создано совокупностью точечных электрических зарядов, то согласно принципу суперпозиции

Е=Е1+Е2+….=ΣЕi .

Равным образом, принцип суперпозиции выполняется и для потенциала:

φ=φ1+φ2+…. =Σφi . (1)

Воображаемые линии в пространстве, касательные к которым в каждой точке совпадают с направлением вектора Е, называются силовыми линиями (линии со стрелками на рис. 3,4).

Важное значение в медицинской практике приобрело электрическое поле диполя. рис1

Диполем будем называть два точечных заряда q, равных по абсолютной величине, но противоположных по знаку, находящихся на расстоянии d друг от друга. Величина d получила название плеча диполя, а вектор р=qd - дипольного момента. За направление диполя принято направление от отрицательного заряда к положительному (рис.1).

Электрическими диполями являются полярные молекулы, например молекула воды, совокупность диполей представляют мембраны клеток, в том числе клетки сердечной мышцы – миокарда. Потенциал реального

диполя может быть найден по формуле (1), где под знаком суммы находятся всего два слагаемых:

φd = qk(1/r1-1/r2) (2)

Рис.1

Если расстояния r1 и r2 будут много больше плеча диполя l, то можно показать [1], что

потенциал может быть найден по приближенной формуле(см. рис.2):

φd ≈ kрcosθ/r2, (3)

где r – среднее расстояние от диполя до точки,

θ – угол, который составляет вектор р с радиусом -вектором r.

Такой диполь получил название точечного. Целью работы является определение потенциала диполя по формуле (2) («измеряется» с помощью компьютера) и сравнение его с рассчитанным значением по формуле (3).

рис2

10. Для установления связи между силовой характеристикой электрического поля - напряжённостью и его энергетической характеристикой - потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: dA = q E dl, эта же работа равна убыли потенциальной энергии заряда q: dA = - dWп = - q d, где d - изменение потенциала электрического поля на длине перемещения dl. Приравнивая правые части выражений, получаем: E dl = -d или в декартовой системе координат

Ex dx + Ey dy + Ez dz = - d, (1.8)

где Ex, Ey, Ez - проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем

откуда

Стоящее в скобках выражение является градиентом потенциала j, т. е.

E = - grad = -Ñ .

Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.

Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М, положение которой определяется радиус-вектором r, равен = q / 4pe0er. Направление радиус-вектора r совпадает с направлением вектора напряженности E, а градиент потенциала направлен в противоположную сторону. Проекция градиента на направление радиус-вектора

Проекция же градиента потенциала на направление вектора t, перпендикулярного вектору r, равна

т. е. в этом направлении потенциал электрического поля является постоянной величиной (= const).

В рассмотренном случае направление вектора r совпадает с направлением

рис. 1.6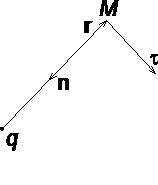

силовых линий. Обобщая полученный результат, можно утверждать, что во всех точках кривой, ортогональной к силовым линиям, потенциал электрического поля одинаков. Геометрическим местом точек с одинаковым потенциалом является эквипотенциальная поверхность, ортогональная к силовым линиям.

При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. На рис. 1.7 приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали - штриховыми.

Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению.