39.Холла эффект

Холла эффект  появление в проводнике с током плотностью j, помещенном в магнитное поле Н, электрического поля E_x, перпендикулярного Н и I. Напряжённость электрического поля (поля Холла) равна:

         E_x = Rhjsin α, (1)

        где α угол между векторами Н и f (α < 180°). Если H ⊥ j, то величина поля Холла E_x максимальна: E_x = RHj. Величина R, называется коэффициентом Холла, является основной характеристикой Х. э. Эффект открыт Э. Г.  ом в 1879 в тонких пластинках золота. Для наблюдения Х. э. вдоль прямоугольных пластин из исследуемых веществ, длина которых l значительно больше ширины b и толщины d,пропускается ток I = jbd (см. рис.); магнитное поле перпендикулярно плоскости пластинки. На середине боковых граней, перпендикулярно току, расположены электроды, между которыми измеряется эдс Холла V_x.

         V_x = E_xb = RHj/d. (2)

         Т. к. эдс Холла меняет знак на обратный при изменении направления магнитного поля на обратное, то Х. э. относится к нечётным гальваномагнитным явлениям ().

         Простейшая теория Х. э. объясняет появление эдс Холла взаимодействием носителей тока (электронов проводимости и дырок) с магнитным полем. Под действием электрического поля носители заряда приобретают направленное движение (дрейф), средняя скорость которого (дрейфовая скорость) v_др ≠ 0. Плотность тока в проводнике j = n․ev_др, где n — концентрация числа носителей, e — их заряд. При наложении магнитного поля на носители действует : F = е [Нv_др], под действием которой частицы отклоняются в направлении, перпендикулярном v_др и Н. В результате в обеих гранях проводника конечных размеров происходит накопление заряда и возникает электростатическое поле — поле Холла. В свою очередь поле Холла действует на заряды и уравновешивает силу Лоренца. В условиях равновесия eE_x = eHv_др,

 

<="" em="" style="border-top-style: none; border-right-style: none; border-bottom-style: none; border-left-style: none; ">отсюда R = 1/ne см³/кулон. Знак R совпадает со знаком носителей тока. Для металлов (См), у которых концентрация носителей (электронов проводимости) близка к плотности атомов (n ≈ 10²² см^-3), R Холла эффект10^-3 см³/кулон, у полупроводников (См. ) концентрация носителей значительно меньше и RХолла эффект10^-5 см³/кулон.Коэффициент Холла R может быть выражен через подвижность носителей (См. ) заряда μ = еτ/m* и удельную электропроводность σ = j/E = env_дрЕ:

         R = μ/σ. (3)

         Здесь m*—  носителей, τ — среднее время между 2 последовательными соударениями с рассеивающими центрами.

         Иногда при описании Х. э. вводят угол Холла φ между током j и направлением суммарного поля Е: tgφ = E_x/E = Ωτ, где Ω — носителей заряда. В слабых полях (Ωτ<< 1) угол Холла φ ≈ Ωτ можно рассматривать как угол, на который отклоняется движущийся заряд за время τ. Приведённая теория справедлива для изотропного проводника (в частности, дляа), у которого m* и τ — постоянные величины. Коэффициент Холла (для изотропных полупроводников) выражается через парциальные проводимости σ_э и σ_д и концентрации электронов n_э и дырок n_д:

         

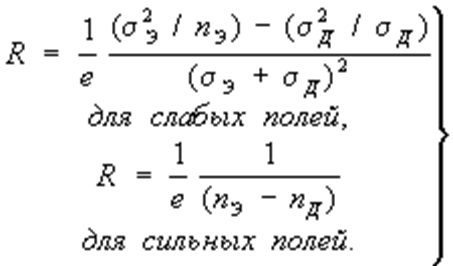
         При n_э = n_д = n для всей области магнитных полей 

R указывает на преобладающий тип проводимости.

         Для металлов величина R зависит от зонной структуры и формы Ферми поверхности (См). В случае замкнутых поверхностей Ферми и в сильных магнитных полях (Ωτ>> 1) коэффициент Холла изотропен, а выражения для R совпадают с формулой 4, б.Для открытых поверхностей Ферми коэффициент R анизотропен. Однако, если направление Н относительно кристаллографических осей выбрано так, что не возникает открытых сечений поверхности Ферми, то выражение для R аналогично 4, б.

         В ферромагнетиках (См. ) на электроны проводимости действует не только внешнее, но и внутреннее магнитное поле: В= Н + 4πМ. Это приводит к особомуферромагнитному Х. э. Экспериментально обнаружено, что E_x= (RB + R_aM) j, где R — обыкновенный, a R_a— необыкновенный (аномальный) коэффициент Холла. Между R_a и удельным электросопротивлением ферромагнетиков установлена корреляция.

         Исследования Х. э. сыграли важную роль в создании электронной теории твёрдого тела (См. ). Х. э. — один из наиболее эффективных современных методов изучения энергетического спектра носителей заряда в металлах и полупроводниках. Зная R, можно определить знак носителей и оценить их концентрацию, а также часто сделать заключение о количестве примесей в веществе, например в полупроводнике. Он имеет также ряд практических применений: используется для измерения напряжённости магнитного поля (см.), усиления постоянных токов (в аналоговых вычислительных машинах (См. )), в измерительной технике (бесконтактный амперметр) и т.д. (подробно см. ).

                 Лит.: Hall Е. Н., On the new action of magnetism on a permanent electric current, «The Philosophical Magazine», 1880, v. 10, p. 301; ЛандауЛ. Д., ЛифшицЕ. М., Электродинамикасплошныхсред, М., 1959; ЗайманДж., Электроныифононы. Теория явлений переноса в твердых телах, пер. с англ., М., 1962; Вайсс Г., физика гальваномагнитных полупроводниковых приборов и их применение, пер. снем., М., 1974; Ангрист Ст., Гальваномагнитные и термомагнитные явления, в сборнике: Над чем думают физики, в. 8. Физика твёрдого тела. Электронные свойства твёрдого тела, М., 1972, с. 45—55.

         Ю. П. Гайдуков.

        

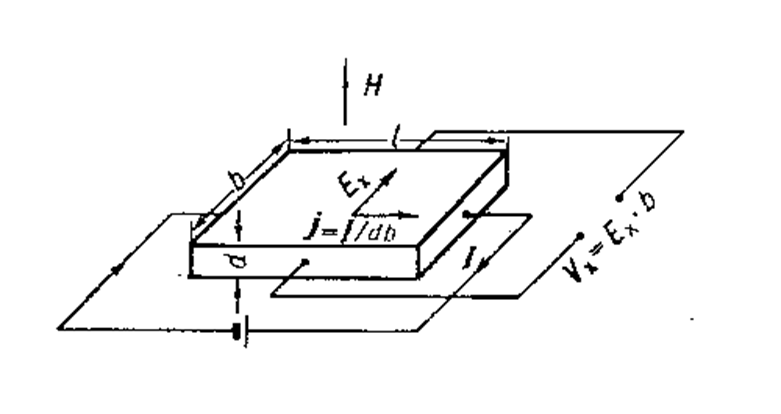
        Рис. к ст. Холла эффект.