12 Билет. Теоремы о свойствах бесконечно малых последовательностей
Свойства
(
n,
n
n)
1 теорема. Произведение бесконечно малой последовательности на ограниченную есть бесконечно малая последовательность.
2 теорема. Сумма двух бесконечно малых является бесконечно малой.
3 теорема. Сумма любого конечного числа бесконечно малых последовательностей является бесконечно малой.
Билет 13. Бесконечно большие последовательности
Последовательность называется бесконечно большой, если для всякого любого числа E>0 существует номер N такой, что для всех членов последовательности с номером n>N выполняется неравенство /an/>E. (ε 0 N n (n N |аn| > ε)).
Если для любого сколь угодно большого положительного числа E, обязательно существует такое N, что для любого следующего числа после N выполняется условие |an > E|
14 Билет. Теоремы о величинах, обратных бесконечно малой и бесконечно большой.
1 теорема. Если последовательность
an
- бесконечно большая,
an
не равно 0, то
последовательность
– бесконечно малая.
1 теорема. Если последовательность
an
- бесконечно малая, an
не равно 0, то
последовательность
бесконечно
большая последовательность.
Из определений бесконечно большой и бесконечно малой последовательностей, следует, что если an – бесконечно большая последовательность, то 1 бесконечно малая, а если an – бесконечно малая последовательность, то – бесконечно большая.
15 Билет. Предел последовательности.
Предел последовательности - элемент того же пространства, который обладает свойством «притягивать», в некотором смысле, элементы данной последовательности.
Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения xn, у которых n>N, удовлетворяют неравенству
|xn - a| < ε.
Сходимость - если у последовательности есть предел, то говорят, что данная последовательность сходится, в противном случае (если у последовательности нет предела) говорят, что последовательность расходится. Сходящиеся последовательности обладают следующим свойством: каждая подпоследовательность сходящейся последовательности сходится, и её предел совпадает с пределом исходной последовательности. Другими словами, у последовательности не может быть двух различных пределов.
Если у множества есть предельная точка, то существует последовательность элементов данного множества, сходящаяся к данной точке. Таким образом, у последовательности может быть несколько предельных точек, но, если последовательность сходится, то все предельные точки совпадают друг с другом и совпадают с пределом самой последовательности.
16 Вопрос. Определение предела последовательности на языке «e» - «n»
Число a называется пределом последовательности {xn}, если для каждого ε > 0 существует такой номер Nε, что для всех n ≥ Nε выполняется неравенство |xn – a| < ε
т. е.
При
этом пишут, что
или
при
n → ∞.
Кратко это определение можно записать
так:
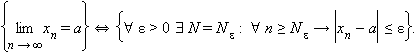
17 Вопрос. Свойства последовательностей, имеющих предел.
Предел суммы равен сумме пределов:
Предел разности равен разности пределов:
Предел произведения равен произведению пределов:
Предел частного равен частному пределов.
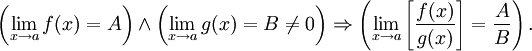
Имеют место следующие арифметические свойства пределов вещественных последовательностей:
,
где k
— константа;
,
если указанные пределы существуют;
при
том же условии;
,
если пределы существуют и
.