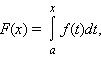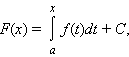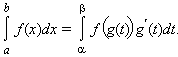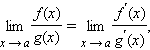- •1 Билет. Понятие множества, элемента множества.
- •2 Билет. Конечные и бесконечные множества.
- •3 Билет. Свойства операций объединения и пересечения множеств.
- •4 Билет. Прямое произведение множеств.
- •5 Билет. Бинарные отношения.
- •6 Билет. Функция как закон соответствия между множествами
- •7. Класс элементарных функций
- •8 Билет. Суперпозиция функций.
- •9. Последовательность - функция натурального аргумента.
- •10. Бесконечно малые последовательности
- •11 Билет. Определение бесконечно малой последовательности на языке «e» - «n»
- •12 Билет. Теоремы о свойствах бесконечно малых последовательностей
- •Билет 13. Бесконечно большие последовательности
- •15 Билет. Предел последовательности.
- •16 Вопрос. Определение предела последовательности на языке «e» - «n»
- •17 Вопрос. Свойства последовательностей, имеющих предел.
- •18 Вопрос. Геометрический смысл предела последовательности.
- •19 Вопрос Теорема о единственности предела последовательности.
- •20 Билет. Теорема о связи последовательности, имеющей предел, её предела и бесконечно малой.
- •21 Билет. Теоремы об арифметических свойствах пределов последовательности:
- •22.Признаки существования предела последовательности.
- •23. Замечательный предел типа «е».
- •24. Предел функции в точке.
- •25 Билет. Определение предела функции на языке языке «ε» — «δ» (предел функции по Коши)
- •26 Билет. Геометрический смысл предела функции в точке.
- •27 Билет. Бесконечно малые и бесконечно большие функции.
- •28 Билет. Свойства функций, имеющих предел.
- •29 Билет. Односторонние пределы функции в точке.
- •30 Билет. Предел функции на бесконечности.
- •31 Билет. Теоремы об арифметических свойствах пределов.
- •32. Сравнение бесконечно малых функций
- •33.«Замечательный» предел - предел отношения синуса бесконечно малого угла к этому углу.
- •34. Определение непрерывности функции в точке.
- •35.Непрерывность функции на отрезке.
- •36 Билет. Определение непрерывности функции через приращения аргумента и функции.
- •37 Билет. Теоремы о свойствах непрерывных функций.
- •38 Билет. Непрерывность основных элементарных функций в каждой точке, где они определены.
- •39 Билет. Первая и вторая теоремы Больцано-Коши.
- •40 Билет. Разрывные функции. Типы разрывов.
- •41 Билет. Определение производной.
- •42 Билет.Приращение функции и вычисление средней скорости изменения функции.
- •43 Билет.Геометрический смысл производной.
- •44 Билет. Связь между непрерывностью и существованием производной.
- •45) Правила вычисления производной от суммы, произведения и частного функций.
- •46 Билет. Производная сложной функции
- •47 Билет. Нахождение производных от элементарных функций
- •48 Билет. Бином Ньютона. Формула Ньютона-Лейбница.
- •49 Билет.Теорема Лагранжа о конечном приращении функции на отрезке.
- •50 Билет. Правило Лопиталя, раскрытия неопределенностей.
- •51 Билет. Понятие о дифференциале функции.
- •52 Билет.Геометрический смысл дифференциала функции.
- •53 Билет. Связь дифференциала и производной функции.
- •54 Билет.Свойства дифференциала.
- •55 Билет.Таблица дифференциалов.
- •60 Билет. Метод интегрирования «по частям» для вычисления неопределенного интеграла.
- •61 Билет. Интегралы, не выражающиеся через элементарные функции.
- •62 Билет. Задача нахождения площади криволинейной трапеции.
- •63 Определенный интеграл как предел интегральных сумм.
- •64 Билет. Производная определенного интеграла по верхнему пределу.
- •64 Билет.Теорема о производной определенного интеграла по переменному верхнему пределу
- •69 Билет. Определение несобственных интегралов с бесконечными пределами.
- •70 Билет. Несобственные интегралы от разрывных функций.
- •71 Билет. Интеграл вероятностей (Пуассона).
48 Билет. Бином Ньютона. Формула Ньютона-Лейбница.
Если
функция f (x)
интегрируема на [a; b],
то для любого
![]() существует
интеграл
существует
интеграл
|
который называется интегралом с переменным верхним пределом.
Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке.
Если
функция f
интегрируема на [a; b]
и непрерывна в
![]() то
функция F (x)
дифференцируема в
то
функция F (x)
дифференцируема в
![]() причем
причем
|
Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида
|
где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.
теорема
Ньютона – Лейбница:
Пусть функция f (x)
непрерывна на [a; b],
а F (x)
– какая-либо первообразная функции f
на этом отрезке. Тогда
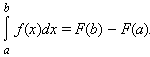
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).
Пусть
f (x)
непрерывна на [a; b],
g (t)
имеет непрерывную производную на [α; β],
![]() Тогда
если a = g (α),
b = g (β),
то справедлива формула
замены переменной в определенном
интеграле:
Тогда
если a = g (α),
b = g (β),
то справедлива формула
замены переменной в определенном
интеграле:
|
Если функции u (x) и v (x) имеют на [a; b] непрерывные производные, то справедлива формула интегрирования по частям:
|
Вычисление определенных интегралов методом, основанным на определении интеграла как предела интегральной суммы, как правило, связано с большими трудностями. Существует более удобный метод, который основан на связи между неопределенным и определенным интегралами.
Теорема. Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нажнем пределах интеграла
Эта формула открывает широкие возможности для вычисления определенных интегралов, поскольку задача вычисления опред.интеграла сводится к задаче исчисления неопред.интеграла, которая достаточно полно изучена.
49 Билет.Теорема Лагранжа о конечном приращении функции на отрезке.
Теорема
Лагранжа.
Если функция f (x)
непрерывна на отрезке [a; b]
и дифференцируема на интервале (a; b),
то существует хотя бы одна точка
![]() такая,
что
такая,
что
|
Это соотношение называется формулой конечных приращений Лагранжа. Воспользовавшись ей, легко доказать, что если производная функции на отрезке [a; b] равна 0, то эта функция постоянна на этом отрезке. Если производная функции f на отрезке [a; b] равна k, то f – линейная функция.
Если в точке x0 функции f и g равны, а производные этих функций, если они существуют, удовлетворяют на некотором отрезке [x0; x1] соотношению f ′ (x) > g′ (x), то в каждой точке промежутка (x0; x1] f (x) > g (x).
50 Билет. Правило Лопиталя, раскрытия неопределенностей.
Пусть
функции f
и g
одновременно являются либо бесконечными
большими, либо бесконечно малыми в точке
a.
Тогда при вычислении пределов
![]() при
x → a
для раскрытия неопределенностей вида
при
x → a
для раскрытия неопределенностей вида
![]() или
или ![]() удобно применить правило
Лопиталя:
удобно применить правило
Лопиталя:
|
Неопределенности вида 0 · ∞, ∞ – ∞, 00, ∞0, 1∞ часто удается свести к неопределенностям вида или с помощью различных преобразований.
51 Билет. Понятие о дифференциале функции.
Дифференциалом
функции f(x)
(обозначается через dF(x)
) называется следующее выражение:![]()
где dx -- дифференциал x при условии, что функция имеет производную.
Предположим,
что существует следующее равенство
функций:![]()
Тогда
дифференциал от равенства есть
![]()
Для решения дифференциальных уравнений используют много разных способов: метод разделения переменных, метод вариации и т.д.
Например,
в методе разделения переменных
используется определение дифференциала
функции т.е.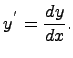
<< Пример 24.1
Найти дифференциал функции ƒ(х)=3x2-sin(l+2x).
Решение: По формуле dy=ƒ'(х) dx находим
dy=(3х2-sin(l+2x))'dx=(6х-2cos(l+2х))dx.
<< Пример 24.2
Найти
дифференциал функции
![]()
Вычислить dy при х=0, dx=0,1.
Решение:
![]()
Подставив
х=0 и dx=0.1, получим
![]()