2.1. Расчет сопротивления судов с умеренной полнотой обводов

Коэффициент остаточного сопротивления рассчитывается по формуле

C_R=C_R()k_k_B/T_B/Tk_Xc ( 2.5.)

Коэффициент C_R() снимается с диаграммы рис. 1, Приложения 1 в зависимости от коэффициента общей полноты и числа Фруда Fr .

Коэффициент k_, учитывающий влияние относительной длины =L/V^1/3 , равен

k_=_/_o, ( 2.6.)

где - _ - снимается с диагpаммы рис.2 Приложение 1 в зависимости от расчетного значения относительной длины  и числа Фруда Fr;

_o - снимается с диаграммы рис. 2 Приложения 1 в зависимости от стандартного значения относительной длины _o , определяемого по диаграмме рис.1 Приложения 1 в функции .

Произведение коэффициентов k_B/T*_B/T , учитывающее влияние отличия расчетного значения B/T от принятого в серии (B/T 2.5) на коэффициент остаточного сопротивления C_R , определяется по диаграмме рис. 3 Приложения 1 в зависимости от отношения B/T и числа Фруда.

k_B/T*_B/T = k_B/T(Fr,B/T)/ _B/T(B/T) (2.7.)

где k_B/T(Fr,B/T) и _B/T(B/T) - снимается с рис.3, Приложения 1.

Коэффициент k_Xc учитывает влияние на коэффициент остаточного сопротивления C_R различий между расчетными значениями относительного положения центра величины по длине судна X_c и стандартного X_Co.

X_Co =-0.015 при  = 0.6

X_Co = 0.005 при  = 0.7

X_Co = 0.02 при  = 0.8

Значения коэффициента k_Xc снимается с диаграммы рис. 4-б или 4-в Приложения 1. Выбор соответствующей диаграммы определяется расчетным значением коэффициента общей полноты .

При промежуточных значениях коэффициента общей полноты  значение коэффициента k_Xc находится интерполяцией между значениями k_Xc, снятыми с двух диаграмм ( рис. 4-а, 4-б, 4-в) для стандартных  , между которыми находится расчетное значение  .

В таблице 2.4. приведен пример расчета буксировочного сопротивления и буксировочной мощности судна с умеренной полнотой обводов, имеющего следующие основные элементы:

L = 184,5 м; B = 29,0 м; d = 10,1 м;  = 0,76; = 0,012; _s = 15,3 уз

Таблица 2.4.

Расчет буксировочного сопротивления и буксировочной мощности.

№ п/п	Обозначение расчётных величин.	Числовые значения расчетных величин.						Примечание
1		0,16	0,17	0,18	0,19	0,2	0,21	Задаемся.
2	, м/с	6,81	7,23	7,66	8,08	8,51	8,93
3	, узлы	13,25	14,07	14,9	15,72	16,56	17,37
4		0,861	1,075	1,277	1,296	1,461	1,655	Приложение1, рис.1
5		1,073	1,06	1,065	1,046	1,029	1,016	Приложение1, рис.4б,4в
6		1,283	1,283	1,283	1,283	1,283	1,258	Приложение1, рис.2
7		1,171	1,171	1,171	1,171	1,171	1,161	Приложение1, рис.2
8		1,096	1,096	1,096	1,096	1,096	1,084
9		1	1	1	1	1	1	Приложение1, рис.3
10		1,022	1,022	1,022	1,023	1,023	1,023	Приложение1, рис.3
11		1,022	1,022	1,022	1,023	1,023	1,023
12		1,03	1,28	1,52	1,52	1,69	1,86
13		7,8	8,29	8,78	9,26	9,75	10,23
14		1,62	1,61	1,6	1,59	1,58	1,57	Рис.2.1
15		0,2	0,2	0,2	0,2	0,2	0,2	Таблица 2.1
16		0,1	0,1	0,1	0,1	0,1	0,1	Таблица 2.2
17		2,95	3,19	3,42	3,41	3,57	3,73
18	, кН	512	624	750	833	967	1112
19	, кВт	3487	4512	5745	6731	8229	9930
Cb = 0,76; B/d = 2,87; = 0,012;  = 1,025 ;  = 7297 м2; L = 184,5 м; d = 10,12 м;  = 1,6110-6 м2/с; V = 41152 м3; = 5,34

Последовательность расчетов сопротивления такова.

1. Рассчитываем и записываем в нижнюю часть таблицы 2.4. постоянные величины расчета для каждого промежуточного значения скорости:

1.1. Число Фруда определяем для заданных значений скорости судна V_s и длины судна L

1.2. Площадь смоченной поверхности

=LT[2+1.37(-0.274)B/T]

где -L, B, T - длина, ширина, осадка судна (м);

 - коэффициент общей полноты.

1.3. Объёмное водоизмещение судна:

V =C_bLBТ (м³).

1.4. Относительная длина:

1.5. Коэффициент Ψ₀ снимаем с графика рис.1 Приложения 1.

1.6. Рассчитываем соотношение ширины судна к его длине:

B/D

2. Задаемся в реальном диапазоне рядом значений относительной скорости судна чисел Фруда) и записываем их в строку 1.В таблицу в первую строку значения Fr выбираются произвольно, так чтобы рассчитанное для исходных данных значение число Фруда было посередине.

3. В строке 2 рассчитываем значения скорости судна в (м/с) для каждого значения числа Фруда:

4. В строке 3 пересчитываем значения скорости судна из (м/с) в (узлы):

4. В строке 4 записываем значения коэффициента C_R(), снятые с диаграммы рис.1 Приложения 1.

5. В строке 5 записываем значения коэффициента k_Xc, найденного интерполяцией между значениями k_Xc, снятыми с диаграмм рис.4б (для =0.7) и рис. 4в (для =0.8) Приложения 1. Так же можно использовать формулу для интерполирования:

y₃=((y₂-y₁)/(0,8-0,7))(C_b-0,7)+y₁,

где y₃ – истинное значение k_Xc ( оно заносится в таблицу 2.4. );

y₂ – значение k_Xc снятое при =0,8;

y₁ – значение k_Xc снятое при =0,7.

Остальные значения рассчитываются аналогично, но подставляются соответствующие значения «y» из таблицы 2.4..

6. В строке 6 записываем значения коэффициента _, снятые с диаграммы рис.2 Приложения 1 в зависимости от числа Фруда и расчетной относительной длины

Поскольку кривые _ построены для чисел Фруда, начиная с Fr=0.2, для меньших Fr значения _ принимаются такими же, как и для Fr=0.2.

7.В строке 7 записываем значения коэффициента _o, снятые с диаграммы рис. 2 в зависимости от стандартного значения _o снятого с рис.1 Приложения 1

8. В строке 8 подсчитываем коэффициент k_=_/_o

9. В строке 10 записываем значения коэффициента k_B/T(B/T, Fr), снятые с диаграммы рис. 3 Приложения1 в зависимости от расчетного отношения B/T и чисел Фруда, записанных в 1 строке.

10. В строке 9 записываем значение коэффициента _B/T, снятые с рис. 3 Приложения 1 в зависимости от отношения B/T.

11. В строке 11 рассчитывается величина по формуле (2.7.)

k_B/T_B/T=k_B/T(B/T,Fr)/_B/T(B/T)=(10)/(9)

где коэффициент k_B/T(B/T,Fr) снимается с диаграммы рис.3 Приложения 1 в зависимости от отношения B/T и числа Фруда, а коэффициент _B/T(B/T) снимается с этой же диаграммы в зависимости от отношения B/T.

12. В строке 12 рассчитывается коэффициент остаточного сопротивления C_R в соответствии с формулой.

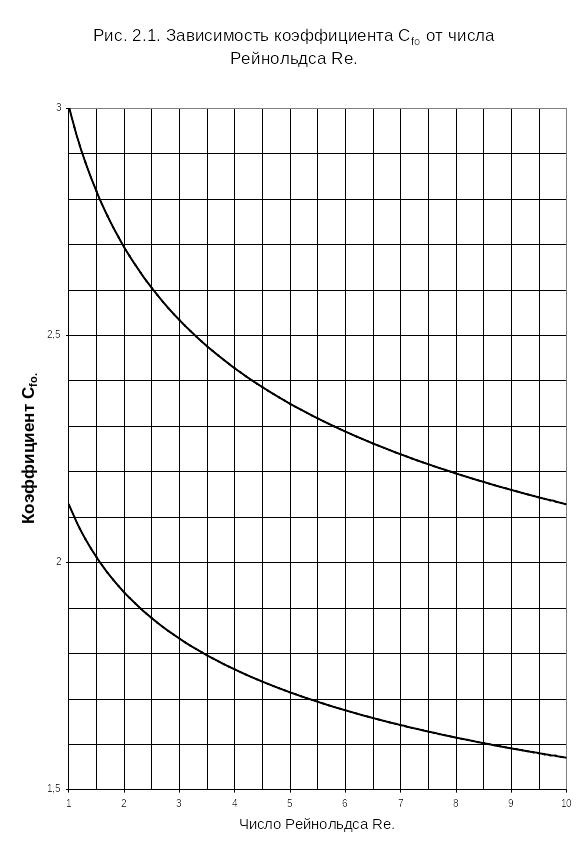
13. В строках 13 и 14 рассчитываются числа Рейнольдса Re и коэффициент C_Fo по формуле (2.3.) или снимается по графикам рис. 2.1.

14. В строках 15 и 16 записываются значения надбавки на шероховатость C_A, значения которой берутся из табл. 2.1. и коэффициент сопротивления выступающих частей, значения которого берутся из табл. 2.2. в зависимости от длины судна.

15. В строке 17 подсчитывается коэффициент полного сопротивления

C=C_R+C_Fo+C_A+C_Ap

16. В строках 18 и 19 подсчитывается буксировочное сопротивление R=0.5C² и буксировочная мощность EPS=R.

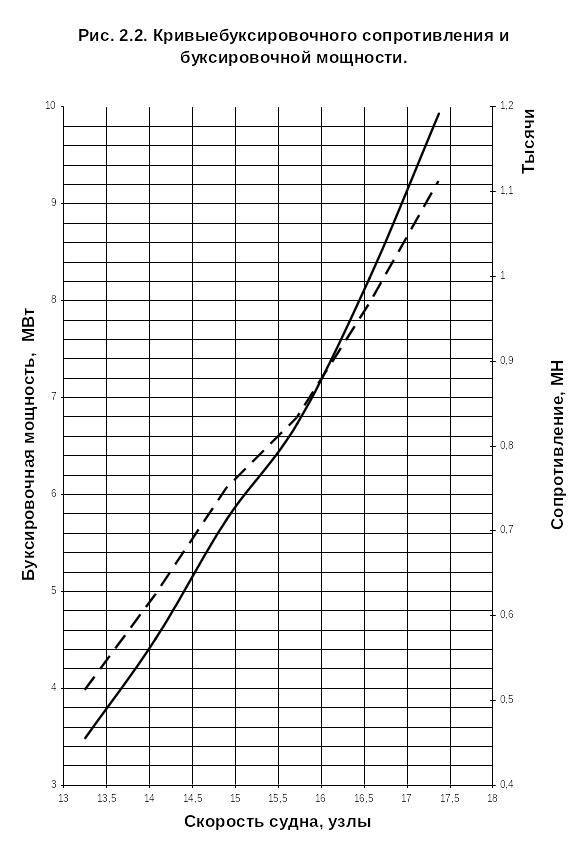
По результатам расчета строятся кривые R(_s) и EPS(_s), которые изображены на рис. 2.2.

Для заданной скорости снимаем с графика рис. 2.2. значения сопротивления R(_s) и буксировочной мощности EPS(_s) при скорости судна _s = 15,3 уз: R= 791 кН;

EPS= 6220 кВт
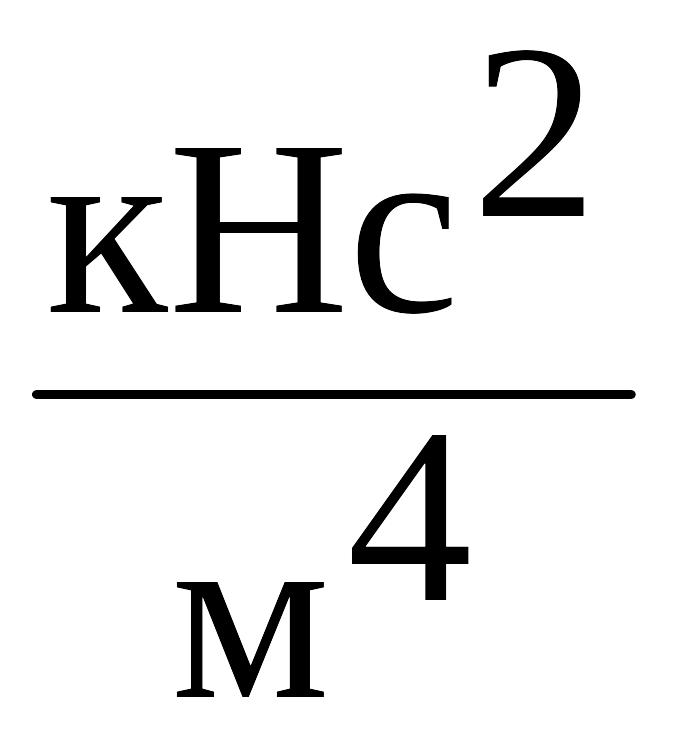