
- •308015, Г. Белгород, ул. Победы, 85.
- •Содержание
- •Введение
- •1.Анализ основных методов расчета зубчатых колес
- •1. 1 Материалы зубчатых колес
- •В табл.1.1 приведены механические характеристики некоторых марок сталей, применяемых для изготовления зубчатых колес.
- •2. Допускаемые напряжения для зубчатых передач при их расчете на выносливость
- •3. Закрытая цилиндрическая прямозубая передача
- •4. Особенности расчета открытых цилиндрических передач
- •5. Расчет закрытой цилиндрической прямозубой передачи Исходные данные
- •5.1. Расчет основных параметров закрытой цилиндрической прямозубой передачи Выбираем материал зубчатых колес, термообработку; определяем допускаемые напряжения для шестерни и колеса.
- •Заключение
- •Список дитературы
4. Особенности расчета открытых цилиндрических передач
Открытые передачи выполняют только прямозубыми и применяют при окружной скорости до 2 м/с. Степень точности их изготовления обычно девятая.
Особенности расчета в сравнении с закрытыми передачами:
4.1. При определении допускаемых напряжений (раздел 2) принимают коэффициент долговечности KHL = KFL = 1.
4.2. При любой твердости рабочих поверхностей зубьев открытые передачи считаются прирабатывающимися. Коэффициенты, учитывающие неравномерность распределения нагрузки по ширине зубчатого венца
KH = KF = 1.
4.3. Перед определением модуля задаются числом зубьев шестерни Z1. Обычно принимают Z1 = 17...22.
4.4. Для цилиндрической передачи модуль определяют по формуле (мм)
![]() ,
,
где а – межосевое расстояние, найденное из условия контактной выносливости зубьев, см. п. 3.4; U – передаточное число открытой пары.
Знак “-” для внутреннего зацепления.
Величина модуля округляется до стандартного значения по табл. 3.2.
5. Расчет закрытой цилиндрической прямозубой передачи Исходные данные
По варианту 00 спроектировать закрытую цилиндрическую прямозубую передачу при следующих исходных данных:
P1 = 11,79 кВт – номинальная передаваемая мощность на валу шестерни;
n1 = 327,3 мин -1 – частота вращения шестерни;
U = 3,64 – передаточное число рассчитываемой пары;
T = 10 лет – ресурс работы передачи;
Ксут = 0,8 – коэффициент суточной нагрузки передачи;
Кгод = 0,9 - коэффициент годовой нагрузки передачи;
нагрузка передачи постоянная, с малыми толчками; передача нереверсивная; пусковая перегрузка не превышает 2,5 раза от номинальной нагрузки.
Кинематические и силовые соотношения в передачах
Как
известно из теоретической механики
линейная скорость точек вращающегося
тела V,отстоящих
от оси вращения на расстоянии D/2,
определяется по формуле
![]()
![]() м/с
м/с
где , с-1 – угловая скорость рассматриваемой точки, равная
Тогда
окружная скорость может быть определена
как
![]() м/с.
м/с.
Силу,
вызывающую вращение тела и направленную
по касательной к его поверхности
(перпендикулярно к радиусу), называют
окружной, или тангенциальной силой Ft,
Н. Связь между этой силой Ft,
окружной скоростью V
и мощностью Р выражается зависимостью
![]() , Вт. P=T
, Вт
, Вт. P=T
, Вт
Вращающий момент Т, Нм определяется по формуле
![]() P,
Вт, ,
с-1 или
P,
Вт, ,
с-1 или
![]() ,
Нм
,
Нм
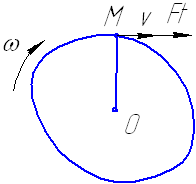
Рис. 5.1. Вращающий момент
КПД и передаточное отношение i механического привода, состоящего из нескольких последовательно работающих передач вращательного движения, определяют следующим образом.
Пусть
в приводе имеется «К» валов и соответственно
«К-1» передач. КПД отдельных передач
равны: ![]()
![]() ;
…….
;
…….
![]() .
.
Перемножим
отдельных передач: ![]()
Следовательно
![]()
КПД привода, состоящего из нескольких последовательно работающих передач, равен произведению КПД всех этих передач.
Передаточные отношения отдельных передач равны:
![]()
![]() ……
……
![]() .
.
Перемножим отдельные передаточные отношения:
![]()
Следовательно,
![]()
Передаточное отношение привода, состоящего из нескольких последовательно работающих передач, равно произведению передаточных отношений всех этих передач.
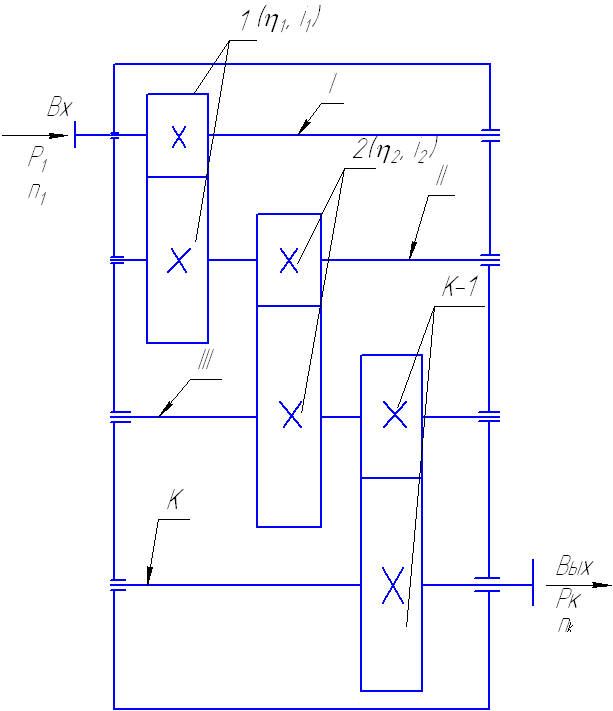
Рис. 5.2. Привод редуктора
Принцип действия и классификация
Зубчатые передачи являются основной разновидностью механических передач, работающих на принципе зацепления с непосредственным касанием ведущей и ведомой деталей – пары зубчатых колёс.
Они с успехом применяются в самых точных и самых тонких приборах, где нагрузка на зубья бывает в долях грамма, а сами колёса имеют диаметр 1 мм, и в самых тяжёлых мощных машинах (краны, станки), где нагрузка измеряется в сотнях тонн, а размеры колёс десятками метров.
Зубчатые передачи классифицируют следующим образом:
по расположению осей валов;
по расположению зубьев на колёсах;
по форме профиля зуба.
По расположению осей валов различают передачи:
с параллельными осями, которые выполняют с цилиндрическими колёсами внешнего или внутреннего зацепления;
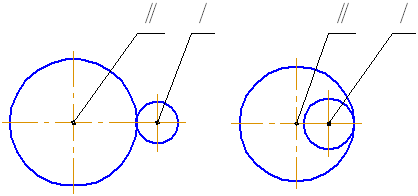
Рис. 5.3. Привод с параллельными осями
По расположению зубьев на колёсах различают: прямозубые, косозубые, шевронные и с круговыми зубьями.
Рис. 5.3. Привод по расположении зубьев
По форме профиля зуба различают: эвольвентные и круговые передачи. Наиболее распространён эвольвентный профиль зуба, предложенный в 1760 году Л. Эйлером. Он обладает целым рядом существенных технологических преимуществ. Круговой профиль зуба предложен М.Л. Новикомым в 1954 году. По сравнению с эвольвентным он позволяет повысить нагрузочную способность зубчатых передач.
Оценка и применение зубчатых передач
Основные преимущества зубчатых передач:
высокая нагрузочная способность и, как следствие
малые габариты;
большая долговечность и надёжность работы (например, для редукторов общего применения установлен ресурс 30 000 ч);
высокий КПД (до 0,97…0,98 в одной ступени);
постоянство передаточного отношения (отсутствие проскальзывания);
возможность применения в широком диапазоне скоростей (до 150 м/с) и мощностей (до десятков тысяч кВт) и передаточных отношений (до н7ескольких сотен тысяч).
Среди недостатков зубчатых передач можно отметить:
повышенные требования к точности изготовления;
шум при больших скоростях;
высокую жёсткость, не позволяющую компенсировать динамические нагрузки.
Отмеченные недостатки не снижают существенного преимущества зубчатых передач перед другими. Вследствие этого зубчатые передачи наиболее широко распространены во всех отраслях машиностроения и приборостроения. Из всех перечисленных выше разновидностей зубчатых передач наибольшее распространение имеют передачи цилиндрическими колёсами, как наиболее простые в изготовлении и эксплуатации, надёжные и малогабаритные. Конические, винтовые и червячные передачи применяют лишь в тех случаях, когда это необходимо по условиям компоновки машины.
Геометрия и кинематика зубчатых передач
Все понятия и параметры, относящиеся к геометрии и кинематике зубчатых передач, стандартизованы. Стандарты устанавливают термины, определения и обозначения, а также методы расчёта геометрических параметров.
Основные параметры. Меньшее из пары зубчатых колёс называют шестерней, а большее – колесом. Термин «зубчатое колесо» общий.
Параметрам шестерни приписывают нижний индекс 1, а параметрам колеса индекс 2.
Кроме того, различают индексы, относящиеся:
к начальной окружной скорости или поверхности;
b к основной поверхности или окрцжности;
a – к поверхности или окружности вершин и головок зубьев;
f – к поверхности или окружности впадин ножек зубьев.
Параметрам, относящиеся к делительной окружности, дополнительного индекса не приписывают.
Общие понятия о параметрах пары зубчатых колёс и их взаимосвязи проще всего уяснить, рассматривая прямозубые колёса. Особенности косозубых колёс учтём дополнительно.
z1 и z2 – числа зубьев шестерни и колеса;
![]() передаточное
число, или отношение большего числа
зубьев к меньшему, используется наряду
с передаточным отношением
передаточное
число, или отношение большего числа
зубьев к меньшему, используется наряду
с передаточным отношением
![]() как удобное при расчёте зубьев по
контактным напряжениям;
как удобное при расчёте зубьев по
контактным напряжениям;
P – делительный окружной шаг зубьев (равный шагу исходной зубчатой рейки);
Pв
– основной шаг зубьев
![]() ;
;
- угол профиля делительный (равный углу профиля исходного контура), по ГОСТ 13755-81 = 20 ;
w
– угол зацепления , или угол профиля
начальный,
![]() ;
;
m
– окружной модуль зубьев (основная
характеристика размеров зубьев). Значения
модулей стандартизованы в диапазоне
0,05…100 мм;
![]() ;
;
d – делительный диаметр (диаметр окружности, по которой обкатывается инструмент при нарезании зубьев),
dв – основной диаметр (диаметр окружности, развёрткой которой являются эвольвенты зубьев, )
dw1, dw2 – начальные диаметры (диаметры окружностей, по которым пара зубчатых колёс обкатывается в процессе вращения),
![]() ;
;
![]() .
.
У передач без смещения и при суммарном смещении Х = 0, т.е. начальные и делительные окружности совпадают:
![]() ;
;
![]() ,
,
аw
– межосевое расстояние пары зубчатых
колёс;
![]()
для
передач без смещения
![]() .
.
где h – высота зуба; da – диаметр вершин зубьев; df – диаметр впадин;
Для колёс без смещения
h = 2,25m
da = d +2m df = d – 2,5m
A1A2 – линия зацепления (общая касательная к основным окружностям);
g длина активной линии зацепления (отсекаемая окружностями вершин зубьев);
П – полюс зацепления (точка касания начальных окружностей и одноимённо точка пересечения линии центров О1О2 с линией зацепления);
NN – производящая прямая. При перекатывании её по основным окружностям точки прямой NN опишут эвольвенты, образующие рабочий профиль зуба.
Все геометрические параметры показаны на рис. 1.
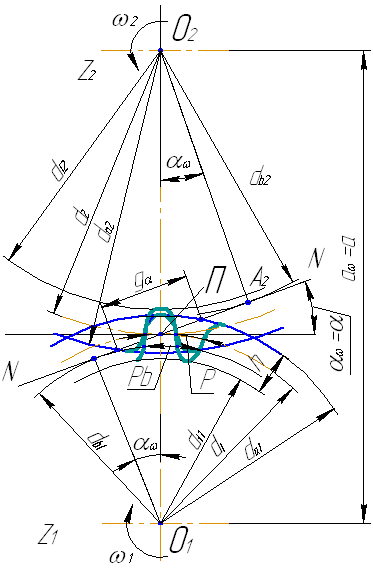
Рис. 5.4. Геометрические параметры зубчатых колес
Коэффициент торцевого перекрытия
Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара входит в зацепление до выхода предыдущей, т.е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность передачи. За период работы пары зубьев точка их зацепления проходит путь, равный длине (рис. 1), а расстояние между профилями соседних зубьев по линии зацепления равно основному шагу РВ. При gPB обеспечивается необходимое перекрытие работы зубьев.
Коэффициентом
торцевого перекрытия
называется отношение длины активной
линии зацепления к основному шагу:
![]()
или
приближённо
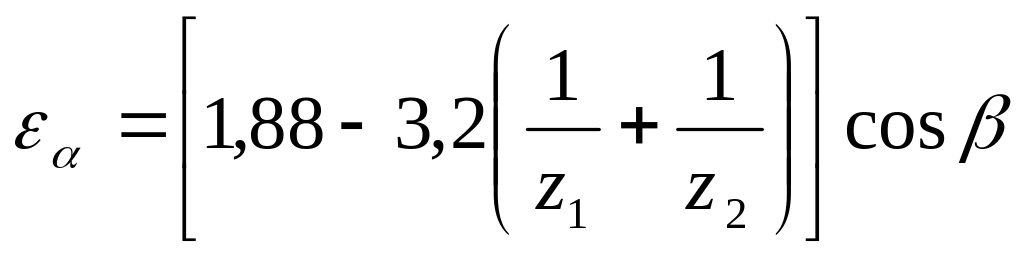 ,
,
где z1, z2 – числа зубьев шестерни и колеса;
- угол наклона линии зуба косозубого колеса.
По условию непрерывности зацепления должно быть 1. С увеличением z увеличивается и .
Прямозубая цилиндрическая передача и силы в зацеплени
В процессе взаимодействия зубчатых колёс полное давление зуба шестерни на зуб колеса направлено по нормали к профилю зубьев в точке их касания. По направлению передаваемое давление совпадает с линией зацепления, образующей с перпендикуляром к линии центров угол зацепления, который в стандартном зацеплении 20 ( = 20 ).
Силы взаимодействия зубьев принято определять в полюсе зацепления П (рис.2), в зоне однопарного зацепления, т.е. когда вся нагрузка передаётся одной парой зубьев. Распределённую по контактным линиям нагрузку в зацеплении заменяют равнодействующей Fn. При этом силами трения в зацеплении пренебрегают ,так как они малы.
Для расчёта зубьев, а также валов и опор силу раскладывают на составляющие: окружную силу - Ft и радиальную силу - Fr.
По заданным моменту Т1 и диаметру d1 определяют окружную силу:
![]()
И через окружную силу выражают все другие
![]() ;
;
![]()
Силы, приложенные к шестерне и колесу с некоторым приближением считают равными по абсолютной величине.
На ведомом колесе направление окружной силы Ft2 совпадает с направлением вращения колеса, а на ведущим окружная сила Ft1 противоположна по направлению 1.
Условия работы зуба в зацеплении
При передаче крутящего момента в зацеплении кроме нормальной силы Fn действует сила трения FTP = Fnf, связанная со скольжением. Под действием этих сил зуб находится в сложном напряжённом состоянии. Решающее влияние на его работоспособность оказывают два основных напряжения: контактные напряжения H и напряжения изгиба F. Для каждого зуба H и F не являются постоянно действующими. Они изменяются во времени по некоторому отнулевому циклу – рис. 5.5.
Время действия F за один оборот колеса (t1) равно продолжительности зацепления одного зуба (t2). Напряжение действует ещё меньшее время. Это время равно продолжительности пребывания в зацеплении данной точки зуба с учётом зоны распространения контактных напряжений.
Переменные напряжения являются причиной усталостного разрушения зубьев: поломка зубьев от напряжений изгиба и выкрашивание поверхности от контактных напряжений. С контактными напряжениями и трением в зацеплении связаны также износ, заедание и другие виды повреждений поверхностей зубьев.
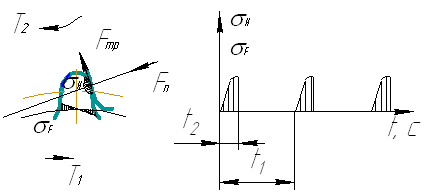
Рис. 5.5.
Виды разрушения зубьев и основные меры их предупреждения
Поломка зубьев. Поломка зубьев связана напряжениями изгиба. На практике наблюдается выламывание углов зубьев вследствие концентрации нагрузки. Различают два вида поломки зубьев: поломка от больших перегрузок ударного действия или даже от статических перегрузок (предупреждают защитой привода от перегрузок или учётом перегрузок при расчёте); усталостная поломка, происходящая от действия переменных напряжений в течение сравнительно длительного срока службы (предупреждают определением размеров из расчёта на усталость). Особое значение имеют меры по устранению концентраторов напряжений (раковин в отливках, микротрещин от термообработки). Общие меры предупреждения поломки зубьев – увеличение модуля, положительное смещение при нарезании зубьев, термообработка, наклёп, уменьшение концентрации нагрузки по краям (жёсткие валы, зубья со срезанными углами).


Рис. 5.6. Повреждения зубчатых колес
Повреждение поверхности зубьев
Все виды повреждения поверхности зубьев связаны с контактными напряжениями и трением.
Усталостное выкрашивание от контактных напряжений является основным видом разрушения поверхности зубьев при хорошей смазке передачи (чаще всего это закрытые, сравнительно быстроходные передачи, защищённые от пыли и грязи).
Зубья таких передач разделены тонким слоем масла, устраняющим металлический контакт. При этом износ зубьев мал. Передача работает длительное время до появления усталости в поверхностных слоях зубьев. На поверхности появляются небольшие углубления, напоминающие оспинки, которые растут и превращаются в раковины. Выкрашивание начинается обычно вблизи полосной линии на ножках зубьев, где нагрузка передаётся одной парой зубьев, а скольжение и перекатывание зубьев направлены так, что масло запрессовывается в трещины и способствует выкрашиванию частиц металла. При выкрашивании нарушаются условия образования сплошной масляной плёнки, появляется металлический контакт с последующим быстрым износом или задиром поверхности.
В передачах, работающих со значительным износом, выкрашивание не наблюдается, так как поверхностные слои снимаются раньше, чем появляются трещины усталости.
Основные меры предупреждения выкрашивания: определение размеров из расчёта на усталость по контактным напряжениям; повышение твёрдости материала путём термообработки; повышение степени точности и в особенности по норме контакта зубьев.
Абразивный износ – основная причина выхода из строя передач при плохой смазке. Это прежде всего открытые передачи, а также закрытые, но недостаточно защищённые от загрязнения. Например, передачи в сельскохозяйственных или транспортных машинах. У изношенной передачи увеличиваются зазоры в зацеплении, появляется шум, возрастают динамические нагрузки. В тоже время прочность изношенного зуба понижается вследствие уменьшения площади его поперечного сечения. Всё это может привести к поломке зубьев, если зубчатые колёса своевременно не заменить.
Расчёт на износ затруднителен тем, что интенсивность износа зависит от многих случайных факторов и, в первую очередь, от интенсивности загрязнения смазки.
Основные меры предупреждения износа – повышение твёрдости поверхности зубьев, защита от загрязнения, применение специальных масел.
Заедание – наблюдается преимущественно у высоконагруженных и высокоскоростных передачах. В месте соприкосновения зубьев этих передач развивается высокая температура, способствующая разрыву масляной плёнки и образованию металлического контакта. Здесь происходит как бы сваривание частиц металла с последующим отрывом их от менее прочной поверхности. Образовавшиеся наросты задирают рабочие поверхности зубьев в направлении скольжения.
Меры предупреждения заедания – те же, что против износа. Желательно плакирование зубьев и интенсивное охлаждением смазки. Эффективно применение противозадирных масел с повышенной вязкостью.
Пластичные сдвиги наблюдаются у тяжело нагруженные колёс, выполненных из мягкой стали. При перегрузках на мягкой поверхности зубьев появляются пластические деформации с последующим сдвигом в направлении скольжения. В результате у полюсной линии зубьев ведомого колеса образуется хребет, а у ведущего соответствующая канавка. Образование хребта нарушает правильность зацепления и приводит к разрушению зубьев.
Пластические сдвиги можно устранить повышением твёрдости рабочих поверхностей зубьев.
Отслаивание твёрдого поверхностного слоя зубьев, подвергнутых поверхностному упрочнению (азотирование, цементирование, закалка). Этот виз разрушений наблюдается при недостаточно высоком качестве термической обработки, когда внутренние напряжения не сняты отпуском или когда хрупкая корка зубьев ни имеет под собой достаточно прочной сердцевины. Отслаиванию способствуют перегрузки.
Во всех перечисленных видах разрушения поверхности зубьев наиболее изучено выкрашивание. Это позволило разработать нормы допускаемых контактных напряжений, устраняющих выкрашивание в течение заданного срока службы. Расчёты по контактным напряжениям, предупреждающие выкрашивание, получили широкое распространение.
В современной методике расчёта из двух напряжений H и F за основное в большинстве случаев принимают контактное напряжение H, так как в пределах заданных габаритов колёс H остаются постоянными, а F можно уменьшать путём увеличения модуля.
Расчётная нагрузка
При работе зубчатых передач вследствие деформации валов, корпусов, опор и самих зубчатых передач, а также неизбежных погрешностей изготовления и монтажа в зацеплении создаются дополнительные динамические нагрузки, а полезная нагрузка распределяется неравномерно по длине зуба. Влияние этих факторов на прочность зубьев учитывается введением при расчёте понятия расчётной нагрузки.
За
расчётную нагрузку принимают максимальное
значение удельной нагрузки, распределённой
по линии контакта зубьев:
![]() ,
,
где: Fn – нормальная сила, направленная по линии зацепления перпендикулярно к рабочим поверхностям зубьев; K – коэффициент расчётной нагрузки; l суммарная длина контактных линий.
Коэффициент расчётной нагрузки определяется как K = KKv,
где: K коэффициент концентрации нагрузки;
Kv коэффициент динамической нагрузки.
Концентрация нагрузки и динамические нагрузки различно влияют на прочность по контактным и изгибным напряжениям. Соответственно различают KH, KH, KHv при расчётах по контактным напряжениям и KF, KF, KFv – по напряжениям изгиба.
Коэффициент концентрации нагрузки К. Концентрация или неравномерность распределения нагрузки по длине зуба связана с деформацией валов, корпусов, опор и самих зубчатых колёс, а также с погрешностями изготовления передачи. Поясним это сложное явление на примере, учитывающем только прогиб валов.
Рассмотрим взаимное расположение зубчатых колёс при деформированных валах в случаях: симметричного, несимметричного и консольного расположения колёс относительно опор. Валы прогибаются в противоположные стороны под действием сил в зацеплении.
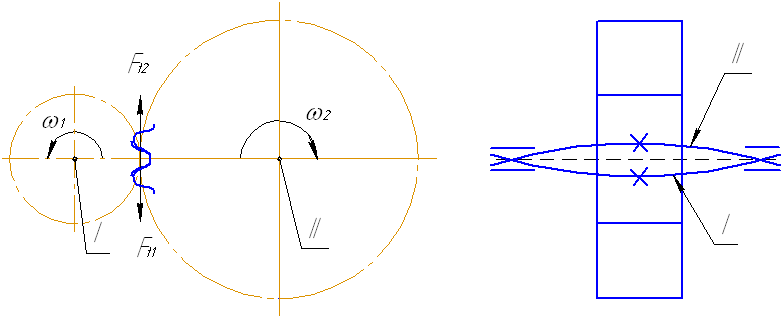
Рис. 5.7. Взаимное расположение опор зубчатых колес
При симметричном расположении опор прогиб балов не вызывает перекоса зубчатых колёс и, следовательно, почти не нарушает распределения нагрузки по длине зуба. Это самый благоприятный случай.
При несимметричном и консольном расположении опор колеса колёса перекашиваются на угол , что привод к нарушению правильного касания зубьев.
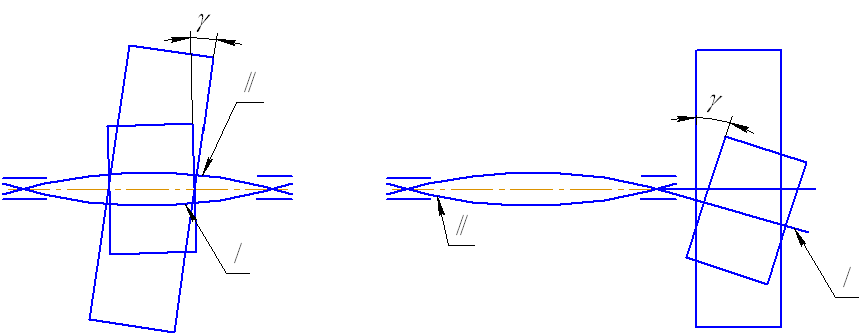
Рис. 5.8. Взаимное расположение при несимметричном и консольном расположении опор зубчатых колес
Если бы зубья были абсолютно жёсткими, то они соприкасались бы с только своими концами. Деформация зубьев уменьшает влияние перекосов и в большинстве случаев сохраняет их соприкасание по свей длине. Однако при этом нагрузка перераспределяется в соответствии с деформацией отдельных участков зубьев.
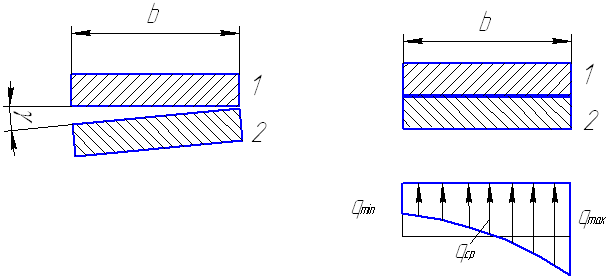
Рис. 5.9. Нагрузки на зубъя колес
Отношение максимальной удельной нагрузки qmax к средней интенсивности нагрузки qcp есть коэффициент концентрации нагрузки К:
![]()
При прочих равных условиях влияние перекоса зубьев увеличивается с увеличением ширины колёс, поэтому её ограничивают.
Если колёса изготовлены из прирабатывающихся материалов (например, стали твёрдостью НВ 350), то концентрация нагрузки постепенно уменьшается вследствие повышенного местного износа. При постоянной нагрузке приработка зубьев может полностью устранить концентрацию нагрузки.
При высокой твёрдости поверхности зубьев (НВ 350) благоприятное влиянием приработки значительно меньше. Меньше приработки и при высоких окружных скоростях (v 15м/с), так как здесь между зубьями образуется масляный слой, защищающий их от износа.
При конструировании передачи необходимо учитывать все факторы, влияющие на концентрацию нагрузки, и в, в первую очередь, не применять нежёстких валов, опор и корпусов.
Расчёт К связан с определением угла прекоса . При этом следует учитывать не только деформацию валов, опор и самих колёс, но также ошибки монтажа и приработку зубьев. Всё это затрудняет расчёт К. Поэтому при инженерных расчётах К определяют по графикам, приводимым в справочной литературе. Графики разработаны для распространённого на практике режима работы с переменной нагрузкой и окружной скоростью v 15 м/с.
При постоянной нагрузке, при НВ 350 и v 15 м/с можно принимать К = 1.
Коэффициент
динамической нагрузки
Kv.
Погрешности нарезания зубьев являются
причиной непостоянства мгновенных
значений передаточного отношения. Это
значит, что при 1
= const,
2
const
и d2/dt
0. В зацеплении появляется дополнительный
динамический момент:
![]()
где: J - момент инерции ведомых масс.
Основное влияние на величину динамических нагрузок имеют ошибки шага. Кроме того, динамические нагрузки зависят от окружной скорости, присоединённых масс, упругости зубьев и пр.
Расчёт коэффициента Kv не менее сложен, чем расчёт К. Для приближённой оценки Kv пользуются таблицами, которые даются в справочной литературе.
Расчёт прочности зубьев цилиндрических передач по контактным напряжениям
Расчёт на прочность цилиндрических передач стандартизован ГОСТ 21354-75. В курсе ДМ изучают основы такого расчёта. При этом вводят некоторые упрощения, мало влияющие на результаты расчётов для большинства случаев практики.
Контактные напряжения возникают в месте соприкосновения двух деталей, когда размеры площадки касания малы по сравнению с размерами деталей (сжатие шаров, цилиндров и т.п.).
Рассмотрим два цилиндра, которые сжимаются удельной нагрузкой q. До приложения нагрузки цилиндры соприкасались по линии. Под нагрузкой q линейный контакт переходит в контакт по узкой площадке. При этом точки максимальных контактных напряжений Н располагаются на продольной оси симметрии контактной площадки. Величину Н вычисляют по формуле Герца:
![]()
где: Н – контактные напряжения; основоположником теории контактных напряжений является H. Yerz (1881 г.). В его честь приписывают нормальным напряжениям индекс «Н», q – удельная расчётная нагрузка; Епр приведенный модуль упругости; коэффициент Пуассона; пр –приведенный радиус кривизны.
Удельная
расчётная нагрузка q
определяется для зубчатой передачи
следующей формулой:
![]()
Здесь
нормальная сила равна
![]()
Суммарная
длина контактных линий
![]()
Тогда
![]()
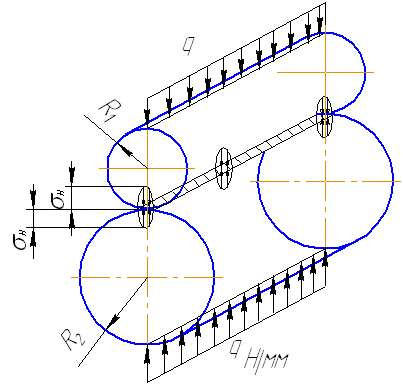
Рис. 5.10. Контактные напряжения зубчатых колес
Обозначим
![]() .
.
t – удельная расчётная окружная сила.
Тогда
расчётная нагрузка q
равна
![]()
где: - торцовый коэффициент перекрытия; К - коэффициент, учитывающий периодическое изменение длины контактных линий.
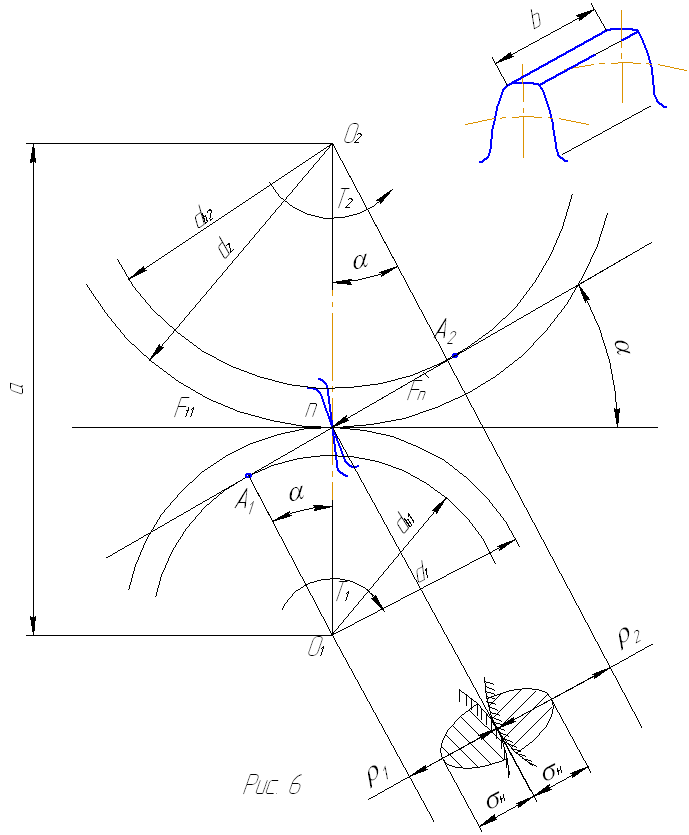
Рис. 5.10. Удельная расчётная нагрузка зубчатых колес
Для распространенных на практике зацеплений величина К = 0,9…1,0.
Приведенный
модуль упругости Епр:
![]()
где: Е1, Е2 – модули упругости материалов обоих колёс.
Приведенный
радиус кривизны пр:
![]()
где: R1, R2 - радиусы кривизны соприкасающихся тел в точках контакта. Знак «+» принимают, когда соприкасающиеся поверхности выпуклые, знак «-« принимают, когда поверхность одного соприкасающегося тела вогнутая.
Исследованиями установлено, что наименьшей контактной выносливостью обладает околополюсная зона рабочей поверхности зубьев. Поэтому расчёт Н принято выполнять в полюсе зацепления (П), где имеет место однопарное зацепление, см. рис. 6.
Контакт
зубьев в полюсе П можно рассматривать
как контакт двух цилиндров с радиусами
1
и 2.
При этом для колёс контактные напряжения
Н
определяются по формуле Герца
![]()
в
которой удельная расчётная нагрузка
q,
как известно:
![]()
Приведенный
радиус кривизны определяем для общего
случая цилиндрического косозубого
зацепления:
![]()
по
рис. 6 для прямозубого зацепления
![]()
![]()
Для
косозубого колеса параметры косого
зуба определяются через параметры
эквивалентного колеса:
![]()
![]()
Тогда в общем случае косозубой цилиндрической передачи:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
где: «+» - для наружного зацепления; «-» - для внутреннего зацепления.
Тогда
имеем
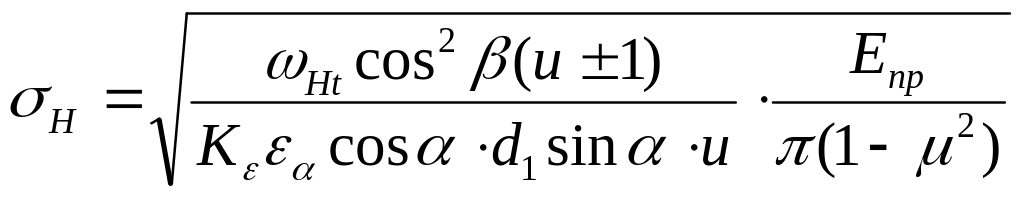 .
.
Известно
![]() .
.
Тогда
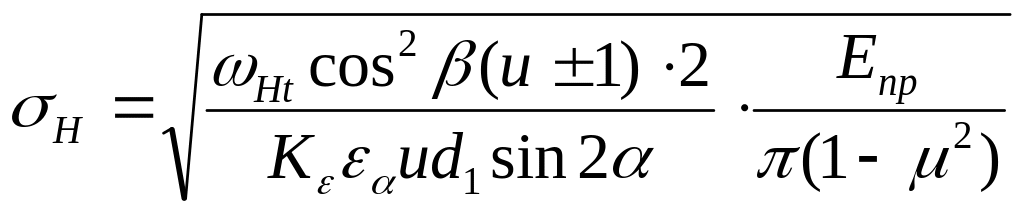 .
.
Обозначим
![]() -
- коэффициент, учитывающий форму
сопряженных поверхностей зубьев;
-
- коэффициент, учитывающий форму
сопряженных поверхностей зубьев;
В передачах без смещения при = 20 ZH= 1,77cos; для прямозубой передачи = 0, ZH= 1,77;
![]() -
коэффициент, учитывающий механические
свойства материалов сопряженных зубчатых
колёс;
-
коэффициент, учитывающий механические
свойства материалов сопряженных зубчатых
колёс;
для стальных колёс: ZM = 275 МПа1/2;
![]() -
коэффициент, учитывающий суммарную
длину контактных линий;
-
коэффициент, учитывающий суммарную
длину контактных линий;
Для прямозубых колёс Z = 1.
При
этих обозначениях получаем:
![]() , МПа
, МПа
Значения расчётных контактных напряжений одинаковы для шестерни и колеса. Поэтому расчёт выполняют для того из колёс пары, у которого меньше допускаемое напряжение Н (чаще это бывает колесо, a не шестерня).
Формулу (1) используют для проверочного расчёта, когда все необходимые размеры и параметры передачи известны. При проектном расчёте необходимо определить размеры передачи по заданным основным характеристикам передачи: крутящему моменту Т, передаточному числу u или мощности и частоте вращения n1 и передаточному числу u.
С этой целью формулу (1) решают относительно делительного диаметра d1 или межосевого расстояния а. При этом в формуле (1) оставляют только те из неизвестных параметров, которые можно определить или выбрать по рекомендациям практики.
Решая
формулу (1) относительно а
заменяем
![]() ,
,
и
вводим коэффициент ba,
полагая
![]() .
.
Удельная
расчётная окружная сила Ht
равна:
![]() .
.
Выразим окружную силу Ft через мощность N1 и частоту вращения n1: :
![]() .
.
Тогда
![]() .
.
После
преобразования получим:
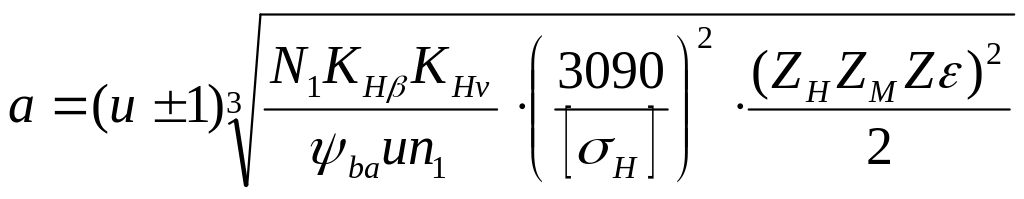 .
.
Обозначим
![]() ,
,
Тогда
межосевое расстояние а
равно
 ,
мм
,
мм
В формуле (2) N1 - мощность на валу шестерни, кВт; n1 - частота вращения шестерни, об/мин (мин-1); Н - допускаемое контактное напряжение, МПа.
Коэффициент К определяют через ZH, ZM, Z.
Для прямозубых колёс при ZH = 1,77, ZM = 275, Z = 1
К 50 МПа1/3;
для косозубых колёс К 43 МПа1/3.
Коэффициент динамической нагрузки КHV при расчёте по фломуле (2) предварительно принимают КHV = 1,1.
Величину коэффициента КH оценивают по специальным графикам в соответствии с заданной схемой передачи.
Коэффициент ширины колеса относительно межосевого расстояния ba выбирают по таблицам.
Для многоступенчатых редукторов, у которых нагрузка увеличивается от ступени к ступени, в каждой последующей ступени ba берут несколько больше, чем в предыдущей. Это способствует хорошему соотношению размеров колёс по ступеням.
Анализ формул (1) и (2) показывает, что контактные напряжения Н зависят от d1 или а, то есть произведения mz1 или произведения m(z1+z2), но не зависят от модуля m или количества зубьев шестерни z1 и колеса z2 в отдельности.
Если НН, то можно увеличивать в рекомендованных пределах ширину колеса b, увеличить делительный диаметр d1 или межосевое расстояние а; можно также изменить материал колёс (взять сталь с большей твёрдостью).
В инженерных расчётах допускается превышение расчётных контактных напряжений Н над допускаемыми напряжениями Н на 5% Н.
Полученное в формуле (2) межосевое расстояние а для нестандартных редукторов округляют по ряду Ra40.
Для стандартных редукторов общего применения, изготавливаемых специализированными заводами, большое значение имеет ограничение числа типоразмера корпусных деталей, когда в одном корпусе можно собрать несколько редукторов. С этой целью установлены стандартные межосевые расстояния а и стандартные значения коэффициента ba.
Расчёт прочности зубьев по напряжениям изгиба
Зуб имеет сложное напряженное состояние. Наибольшие напряжения изгиба F имеют место у корня зуба в зоне перехода эвольвенты в галтель. Здесь же наблюдается концентрация напряжений.
Для того, чтобы достаточно просто получать расчётные зависимости, принимают следующие допущения:
1. Вся нагрузка в зацеплении передаётся одной парой зубьев и приложена к вершине зуба. Практика подтверждает, что этот случай – худший.
2. Сила трения Fтр между зубьями мало влияет на прочность зубьев и учитывается с помощью некоторых поправок.
3. При зацеплении зуба вершиной направление силы Fn определяется углом ’ = + . Но очень мал, и его не учитывают.
4. Зуб рассматривается как консольная балка, для которой справедлива гипотеза плоских сечений и методы сопротивления материалов. В действительности зуб подобен короткой балке переменного сечения, у которой размеры поперечного сечения соизмеримы с размерами высоты. Точный расчёт напряжений в таких элементах выполняют методами теории упругости.
При этих допущениях определяем напряжения изгиба в опасном сечении, расположенном вблизи хорды основной окружности.
Положение опасного сечения определяется методом вписывания в контур зуба параболического бруса равного сопротивления изгибу с вершиной в точке А. Сечение ВС, проведенное через точки, в которых парабола касается боковых контуров зуба, будет опасным, так как во всех сечениях напряжение от изгиба будут меньшими
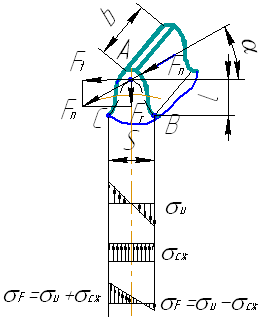
Рис. 5.10. Напряжения изгиба в опасном сечении зубчатых колес
Максимальные
напряжения в точке С
опасного сечения будут равны:
![]() , а в точке В:
, а в точке В:
![]() .
.
За
расчётное напряжение принимают напряжения
в точке В,
так как в большинстве случаев практики
именно здесь возникают усталостные
трещины (для стали растяжение опаснее
сжатия):
![]() .
.
Далее
![]() ,
,
где:
КТ
– теоретический коэффициент концентрации
напряжений; Ftl
– изгибающий момент в опасном сечении;
W
– момент сопротивления изгибу:
![]() ; A
– площадь опасного сечения: A=
b
S.
; A
– площадь опасного сечения: A=
b
S.
Тогда
![]() .
.
Размерные
величины l
и S
неудобны для расчётов. Используя
геометрическое подобие зубьев различного
модуля, эти величины выражают через
безразмерные коэффициенты:
![]() ;
;
![]() ,
,
где m – модуль.
Получим
![]() .
.
Для учёта динамических нагрузок, неравномерностей распределения по длине зуба введём коэффициенты расчётной нагрузки:
![]() ,
,
но
![]() - удельная расчётная окружная сила.
- удельная расчётная окружная сила.
Обозначим
![]() ,
,
где YF – коэффициент формы зуба.
YF зависит от формы зуба, от количества зубьев, от смещения инструмента; YF выбирается по таблицам или определяется по графикам.
Для прямозубых передач тогда получим расчётную формулу:
![]() ,
МПа
,
МПа
У
косозубых передач суммарная длина
контактных линий l
больше ширины колеса, что уменьшает
напряжения изгиба:
![]() .
.
Обозначим Y - коэффициент, учитывающий перекрытие зубьев:
![]() ;
;
![]() ;
;
 ;
;
Y
- коэффициент, учитывающий наклон зубьев:
![]() .
.
Тогда
для косозубой передачи получаем:
![]() ,
МПа
,
МПа
Для
колёс с косыми зубьями YF
определяется по тем же, что и для
прямозубых колёс таблицам или графикам,
но по числу зубьев соответствующего
эквивалентного колеса:
![]() .
.
Для
колёс с внутренними зубьями:
![]() .
.
При
расчёте на изгиб проверяют то из колёс
пары, у которого меньше отношение
F/YF.
Условие равнопрочности по напряжениям
изгиба зубьев шестерни и колеса:
![]() .
.
Влияние числа зубьев на форму и прочность зубьев
В зависимости от числа зубьев z форма эвольвентного профиля зуба меняется. На рисунке показано изменение формы зуба в зависимости от числа зубьев при постоянном модуле (смещения инструмента нет). При z колесо превращается в рейку, и зуб приобретает прямолинейные очертания. С уменьшением числа зубьев z уменьшается и толщина зуба у основания и вершины, а также увеличивается кривизна эвольвентного профиля. Такое изменение формы приводит к уменьшению прочности зуба. При дальнейшем уменьшении количества зубьев z появляется подрезание ножки зуба. При нарезании зубьев инструментом реечного типа для прямозубых передач число зубьев на границе подрезания zmin = 17.
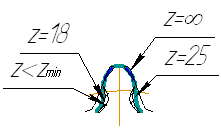
Рис. 5.10. Число зубьев на границе подрезания зубчатых колес
Рассмотренное влияние числа зубьев на прочность справедливо при постоянном модуле, когда с увеличением z увеличиваются и диаметры колёс. При постоянных диаметрах колёс с изменением числа зубьев z изменяется и модуль m. В этом случае изменяется не только форма, но и размеры зуба. С увеличением количества зубьев z форма улучшается, а размеры уменьшаются, так как уменьшается модуль m. Уменьшение модуля m снижает прочность зуба на изгиб.
Особенности расчёта открытых цилиндрических и конических передач
Открытые передачи выполняют только прямозубыми и применяют при окружной скорости до 2 м/с. Степень точности их изготовления обычно 9-ая.
1. При определении допускаемых напряжений коэффициент долговечности принимают KHL=KFL=1
2. При любой твёрдости рабочих поверхностей зубьев открытые передачи считаются прирабатывающимися. Коэффициенты, учитывающие неравномерность распределения нагрузки по ширине зубчатого венца KH = KF = 1
3. Перед определением модуля задаются числом зубьев шестерни.
z1 = 17…22.
4. Для цилиндрической передачи модуль определяют по формуле
![]() ;
;
где: а
– межосевое расстояние, наёденное из
условия контактной выносливости зубьев;
u
– передаточное число открытой передачи:
![]() .
.
Величина модуля округляется до стандартного значения. Дальнейший расчёт ведётся как у закрытой передачи.
У
конической передачи определяется
внешний окружной модуль:
![]()
где de1 – внешний делительный диаметр шестерни; mte округляется до стандартного значения. Дальнейший расчёт как у закрытых передач.
Различие в расчётах закрытых и открытых передач определяется разными условиями работы: открытые передачи работают с худшей смазкой, в атмосфере запылённости. Они больше подвержены абразивному износу.
Допускаемые напряжения при расчёте на усталость
Практика эксплуатации и испытаний позволила установить, что контактная прочность, а следовательно, и допускаемые контактные напряжения определяются в основном твёрдостью рабочих поверхностей зубьев.
Допускаемые
контактные напряжения
для передач, работающих длительное
время определяют по зависимости
![]() ,
,
где: Hlimb – базовый предел контактной выносливости, принимается по таблицам;
SH – коэффициент безопасности, SH = 1,1 – при нормализации, улучшении или объёмной закалке зубьев; SH = 1,2 – при поверхностной закалке, цементации, азотировании;
KHL
– коэффициент долговечности. Для
длительно работающих передач KHL
= 1, для кратковременно работающих
передач:
![]() ;
;
NH0 – базовое число циклов;
NH – число циклов напряжений за время работы.
При большой разнице в твёрдости зубьев шестерни и колеса за расчётное принимается меньшее из двух допускаемых напряжений, определяемых по материалу шестерни Н1 и колеса Н2.
Для передач с непрямыми зубьями, если твёрдость зубьев колеса значительно меньше твёрдости зубьев шестерни (на 100 и более единиц по шкале Бринеля), то в качестве расчётного принимается среднее из Н1 и Н2, но не более 1,25Н2 для цилиндрических и 1,15Н2 – для конических передач:
![]() -
для цилиндрической передачи
-
для цилиндрической передачи
![]() -для
конической передачи
-для
конической передачи
Допускаемые
напряжения изгиба для
расчёта передачи на прочность при
длительной работе определяются по
формуле: ![]() ,
,
где:
Flimb
– базовый предел выносливости по излому
от напряжений изгиба (выбирается по
таблицам); SF
– коэффициент безопасности, рекомендуется
SF
= 1,7…2,2 (верхние значения для литых
заготовок); KFC
– коэффициент, учитывающий влияние
двустороннего приложения нагрузки, KFC
= 1 – односторонняя нагрузка и KFC
= 0,8…0,7 – двух сторонняя нагрузка; KFL
– коэффициент долговечности. Для
длительно работающих передач KFL
= 1. При НВ
350
![]() ,
,
при
НВ
350
![]()
NF0 = 4 106 – базовое число циклов для всех сталей.
