Обернені тригонометричні функції. Тригонометричні рівняння.

1. Обернена функція.

2. Графік і властивості функції .

3. Графік і властивості функції .

4. Графік і властивості функції .

5. Графік і властивості функції .

6. Рівняння з оберненими тригонометричними функціями.

7. Основні найпростіші тригонометричні рівняння.

8. Лінійне рівняння.

9. Зведення тригонометричного рівняння до алгебраїчного.

10. Розкладання рівняння на множники.

11. Рівність однойменних функцій.

12. Перетворення добутків у суми, а сум у добуток.

13. Рішення, засновані на обмеженості функцій.

14. Системи тригонометричних рівнянь.

Питання для самоперевірки.

Вправи для самостійного розв’язування.

1. Обернена функція

Нехай функція неперервна і монотонна на інтервалі і при цьому перемінна змінюється на інтервалі . Розв'яжемо рівняння відносно і знайдемо рішення . Функція називається оберненою до функції . При зазначених умовах обернена функція існує і неперервна при . При цьому справедливі рівності

, ;

, (1)

Графіки функцій , розташовані симетрично щодо бісектриси першого координатного кута.

Приклад. Функція , визначає залежність між перемінними , котру також можна задати рівнянням , . У прикладі , . Рівності (1) приймає вид

, ;

, .

Графіки функцій , розташовані симетрично щодо бісектриси першого координатного кута (Рис. 1).

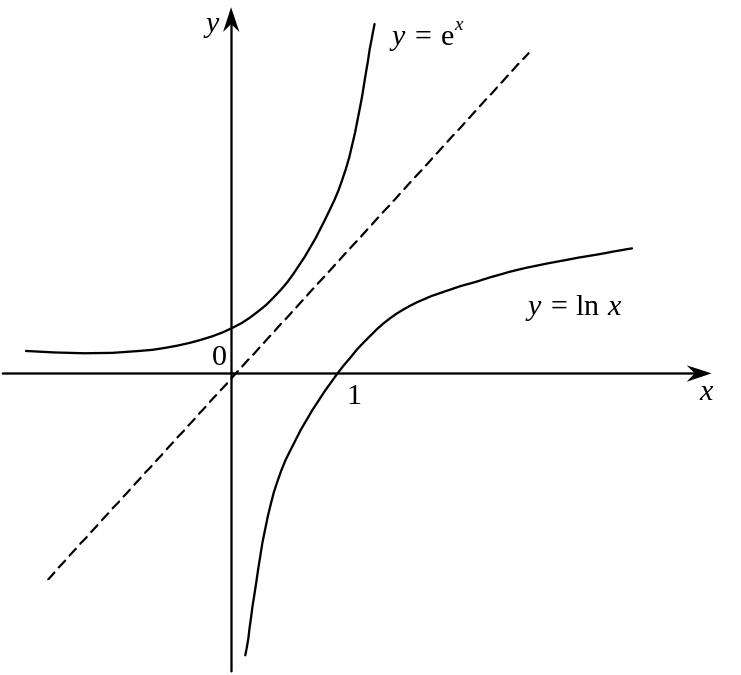
Рис. 1.

2. Графік і властивості функції .

Функція монотонна при . Обернена до неї функція , називається арксинусом (рис. 2).

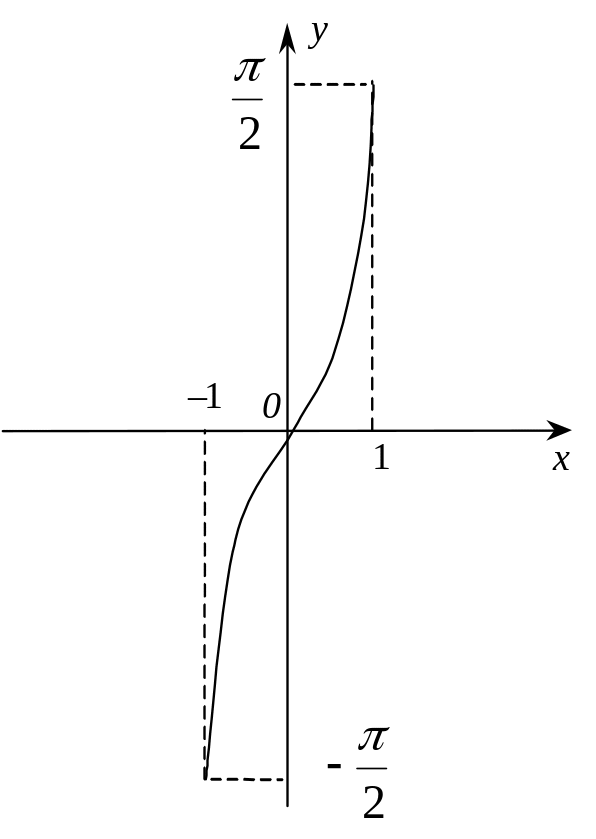
Рис. 2.

Функція монотонно зростає на відрізку і задовольняє нерівності

(2)

Визначення. Арксинусом називається кут , що задовольняє нерівності (2), синус якого дорівнює .

, . (3)

Приведемо деякі числові значення , що задовольняє нерівності (2), синус якого дорівнює .

, , ,

, . (4)

Функція — непарна, тобто

. (5)

Приведемо деякі формули

, ,

, ,

, ,

, , .

Приклад. Обчислити . Одержимо .

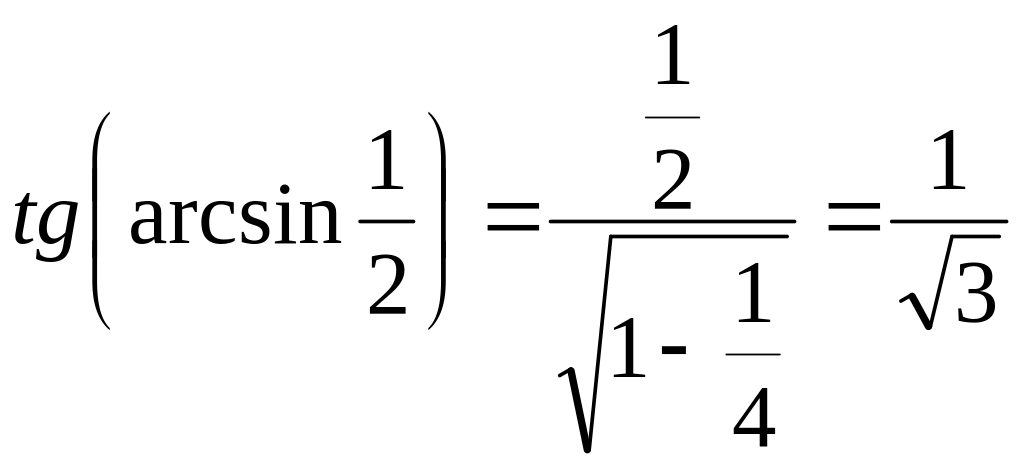Приклад. Вирішити нерівність . Маємо: ; . Оскільки є обмеження , то одержимо відповідь: .

3. Графік і властивості функції .

Функція монотонна при . Обернена до неї функція , називається арккосинусом (Рис. 3)

Рис. 3.

Функція монотонно спадає на відрізку і задовольняє нерівності

(6)

Визначення. Арккосинусом називається кут , що задовольняє нерівності (6), косинус якого дорівнює , тобто

, . (7)

Із симетрії графіка відносно точки випливає рівність:

.

Звідки знаходимо формулу

. (8)

Порівнюючи графіки функцій та дістаємо :

, . (9)

Наведемо деякі числові значення .

, , ,

, (10)

Приведемо формули:

; ;

; ;

, ,

, . (11)

Приклад. Обчислити значення функції

.

Приклад. Обчислити значення функції

.

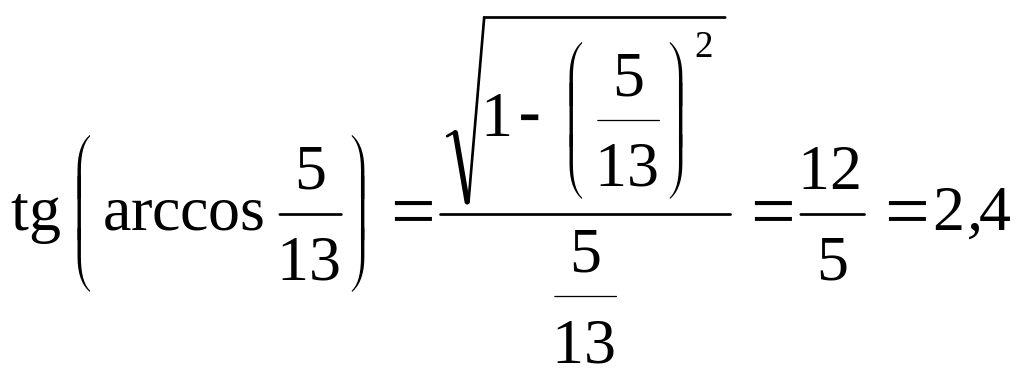4. Графік і властивості функції

Функція монотонна при . Обернена до неї функція , називається арктангенсом (рис. 4).

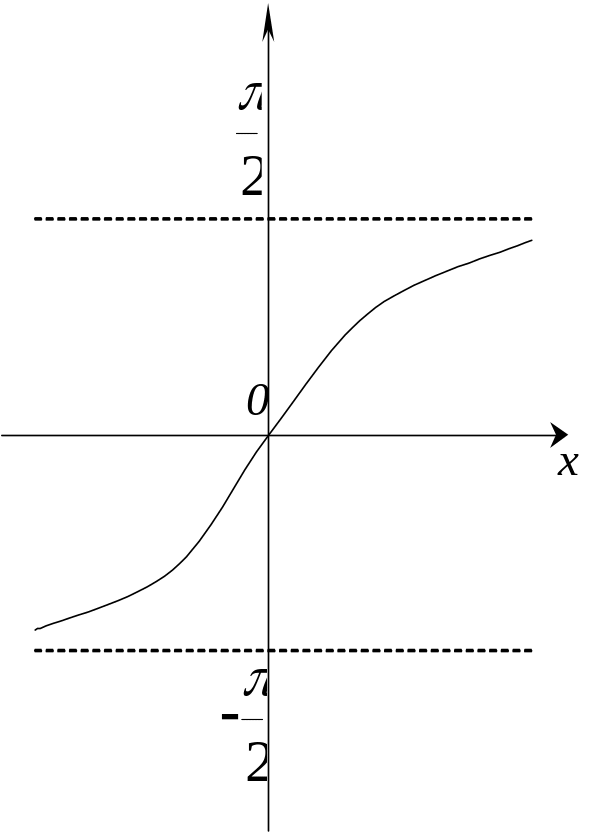
Рис. 4.

Функція монотонно зростає, непарна і задовольняє нерівності

. (12)

Виконано граничні співвідношення

, . (13)

Визначення. Арктангенсом називається кут , що задовольняє нерівності (12), тангенс якого дорівнює , тобто

, . (14)

Функція приймає наступні значення:

, , ;

, . (15)

Приведемо деякі формули:

; ,

; ,

; ,

; , . (16)

Приклад. Обчислити значення:

.

Приклад. Обчислити значення суми

.

Виведемо формулу для суми арктангенсів.

Нехай справджується рівність .

Знаходимо значення

.

Звідси знаходимо формулу

. (17)

Оскільки виконуються нерівності (12), те число K може набувати значень , .

Приклад. Знайти значення суми

.

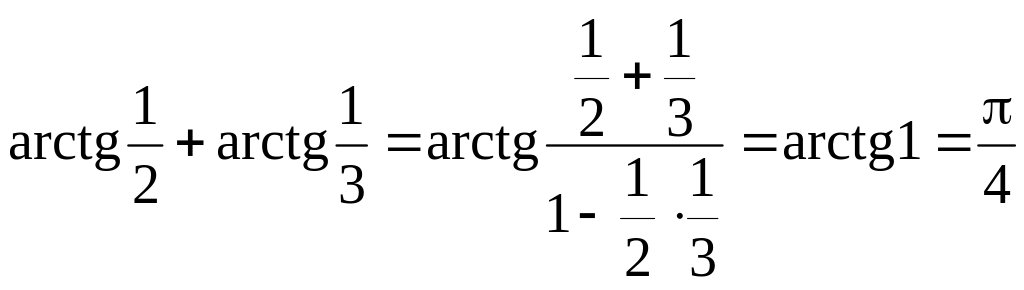Приклад. Знайти значення суми

.