Зміст:

1. Побудова гістограм частот 3

2. Знаходження оцінок математичних сподівань і дисперсій генеральних сукупностей 7

3. Оцінка невідомих математичних сподівань М[Х] і M[У] генеральних сукупностей Х і У за допомогою довірчого інтервалу з надійністю 0,95 15

4. Перевірка гіпотези про рівність дисперсій генеральних сукупностей для вибірок X та Y 19

5. Побудова нормальних кривих за вибірками з генеральних сукупностей Х і Y 20

6. Перевірка гіпотези про нормальний розподіл генеральних сукупностей X та Y, використовуючи критерій погодженості Персона 24

7. Перевірка гіпотези про рівність нулю математичних сподівань генеральних сукупностей Х і У 26

8. Оцінка відхилення емпіричного розподілу від нормального 28

9. Математична модель вибірок 32

10. Висновки 34

Розглянемо вибіркову сукупність Х(додаток 1).

X
-0,266	-1,309	0,597	0,989	0,934
0,901	1,531	-0,889	-1,019	0,084
-1,433	-1,008	-0,99	0,09	0,94
1,327	0,763	-1,724	-0,709	1,1
-0,248	0,788	-0,577	0,122	-0,536
-0,401	-0,679	0,921	0,476	1,121
0,344	-0,324	0,686	-1,487	-0,126
0,441	-0,372	-1,336	0,062	1,506
0,824	0,04	-1,734	0,251	0,054
1,385	1,32	-0,509	-0,381	-1,671

Відсортуємо значення вибіркової сукупності Х за зростанням:

-1,734	-1,724	-1,671	-1,487	-1,433
-1,336	-1,309	-1,019	-1,008	-0,99
-0,889	-0,709	-0,679	-0,577	-0,536
-0,509	-0,401	-0,381	-0,372	-0,324
-0,266	-0,248	-0,126	0,04	0,054
0,062	0,084	0,09	0,122	0,251
0,344	0,441	0,476	0,597	0,686
0,763	0,788	0,824	0,901	0,921
0,934	0,94	0,989	1,1	1,121
1,32	1,327	1,385	1,506	1,531

Розглянемо вибіркову сукупність Y(додаток 1).

Y
1,079	-0,656	-0,999	-0,036	-0,537
1,531	-0,144	-1,92	0,678	-0,402
0,207	-0,745	0,638	1,469	1,214
-1,346	-0,946	-0,157	0,522	-1,264
0,293	1,207	-2,243	1,642	1,353
-0,864	0,128	-0,551	-0,872	1,511
0,803	-0,961	0,183	-0,358	-0,184
-0,315	-0,112	-0,452	1,594	-0,264
-0,379	1,298	-0,126	0,104	-0,529
-0,524	-0,805	1,348	0,676	0,799

Відсортуємо значення вибіркової сукупності Y за зростанням:

-2,243	-1,92	-1,346	-1,264	-0,999
-0,961	-0,946	-0,872	-0,864	-0,805
-0,745	-0,656	-0,551	-0,537	-0,529
-0,524	-0,452	-0,402	-0,379	-0,358
-0,315	-0,264	-0,184	-0,157	-0,144
-0,126	-0,112	-0,036	0,104	0,128
0,183	0,207	0,293	0,522	0,638
0,676	0,678	0,799	0,803	1,079
1,207	1,214	1,298	1,348	1,353
1,469	1,511	1,531	1,594	1,642

1. Побудова гістограм частот

Для наочного зображення статистичного розподілу використовують різні графіки, зокрема, полігон і гістограму.

Гістограму будують у випадку неперервної ознаки, що вивчається. Для цього інтервал, на якому знаходяться всі значення ознаки, що спостерігаються, розбивають на декілька часткових інтервалів довжиною h і для кожного інтервалу знаходять суму частот варіант, що попали в і-й інтервал.

Визначається розмах варіації R

(1.1)

Далі вибирається число часткових інтервалів N. Для того, щоб згрупований ряд був не занадто громіздким, число інтервалів N вибирають за формулою Стреджеса:

, де п - число варіант вибіркової сукупності.

Далі визначається довжина часткового інтервалу

(1.2)

За початок першого інтервалу рекомендується брати величину

(1.3)

Верхня границя останнього інтервалу повинна задовольняти вимогу

(1.4)

Проміжні інтервали отримують, додаючи до кінця поререднього інтервалу довжину часткового інтервалу h.

Гістограмою частот називають сходинкову фігуру, що складається з прямокутників, основами яких є часткові інтервали довжиною h, а висоти дорівнюють n_i/h (густина частоти). Площа часткового i-го прямокутника дорівнює - сумі частот варіант, що попали в i-ий інтервал.

Площа гістограми частот дорівнює сумі всіх частот, тобто об'єму вибірки п.

Побудова гістограми частот вибіркової сукупності Х:

Розіб’ємо вибіркову сукупність на інтервали.

Знаходимо розмах варіації R.

(1.5)

Кількість часткових інтервалів визначимо за формулою Стреджеса:

Знаходимо довжину часткового інтервалу

За початок відліку візьмемо . Знаходимо інтервали.

Таблиця №1

Частковий інтервал, xi – xi+1

( )-( )

( )-( )

( )-( )

( )-( )

( )-( )

( )-( )

( )-( )

( )-( )

Створюємо таблицю для побудови гістограми частот

Таблиця №2

Номер інтервалу, і	Частковий інтервал, xi – xi+1	Сума частот варіант інтервалу, ni	Густина частоти,
1	( )-( )	3	6,12
2	( )-( )	6	12,24
3	( )-( )	7	14,23
4	( )-( )	7	14,23
5	( )-( )	9	18,37
6	( )-( )	10	20,41
7	( )-( )	6	12,24
8	( )-( )	2	4,08

Будуємо гістограму частот вибіркової сукупності Х:

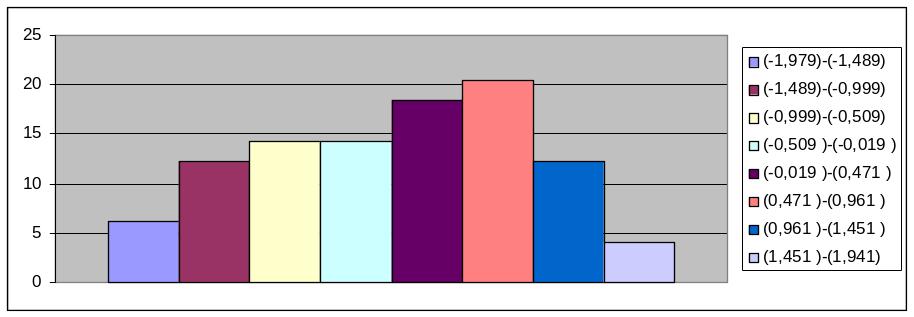
Рис. 1

Побудова гістограми частот вибіркової сукупності Y:

Розіб’ємо вибіркову сукупність на інтервали.

Знаходимо розмах варіації R.

Кількість часткових інтервалів визначимо за формулою Стреджеса:

Знаходимо довжину часткового інтервалу

За початок відліку візьмемо . Знаходимо інтервали.

Таблиця №3

Частковий інтервал, yi – yi+1

( )-( )

( )-( )

( )-( )

( )-( )

( )-( )

( )-( )

( )-( )

( )-( )

Створюємо таблицю для побудови гістограми частот

Таблиця №4

Номер інтервалу, і	Частковий інтервал, yi – yi+1	Сума частот варіант інтервалу, ni	Густина частоти,
1	( )-( )	1	1,72
2	( )-( )	1	1,72
3	( )-( )	8	13,79
4	( )-( )	12	20,69
5	( )-( )	11	18,97
6	( )-( )	6	10,34
7	( )-( )	8	13,79
8	( )-( )	3	5,17

Будуємо гістограму частот вибіркової сукупності Y:

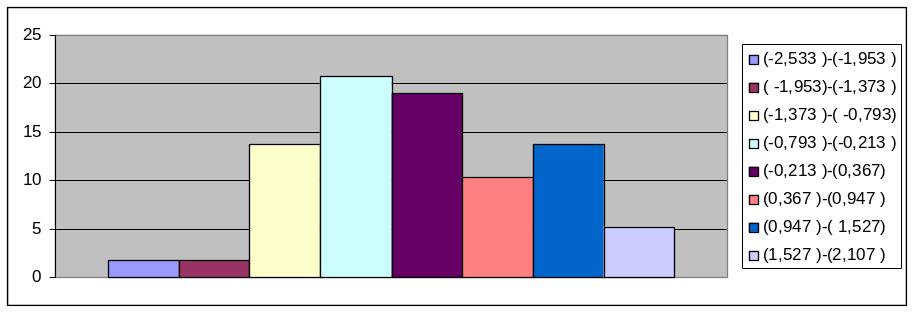
Рис. 2

Висновок: При виконанні завдання для кожної вибірки були побудовані гістограми частот. Площа кожного часткового і-го прямокутника, на гістограмі, – це сума частот варіант, що потрапили у даний інтервал. Площа кожної гістограми частот дорівнює сумі всіх частот, тобто об’єму відповідної вибірки.