- •Разработка алгоритмов и программ решения алгебраических задач численными методами
- •Содержание
- •Задание
- •Анализ задания
- •Теоретические сведения
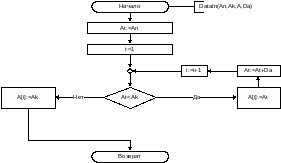
- •Схемы алгоритмов
- •Подпрограмма-процедура предназначенная для заполнения массива параметра а
- •Подпрограмма-функция f предназначена для вычисления значения подынтегральной функции.
- •Подпрограмма-процедура Integral предназначена для вычисления численного значения интеграла.
- •Подпрограмма-процедура Tab предназначена для вычисления таблицы значений функции y.
- •Подпрограмма-процедура RezOut предназначена для вывода результатов выполнения программы на внешние носители.
- •Текст программы на языке программирования Pascal и результаты её выполнения
- •Результат выполнения программы.
Московский авиационный институт
Факультет радиоэлектроники
Кафедра 403
Разработка алгоритмов и программ решения алгебраических задач численными методами
Расчетно-графическая работа по дисциплине «Информатика»
Вариант №5
Выполнил:
Студент группы 4О-110Б
Доценко М.В.
Принял:
Преподаватель кафедры 403
Кошелькова Л.В.
Москва
2012 г.
Содержание
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание
Разработать
схему алгоритма, составить Pascal-программу
вычисления таблицы значений функции
 при заданных изменениях значений
аргумента X
и параметра A,
начальном значениях параметра A,с
шагом Da,
конечном значении параметра A
числе значений аргумента X
и параметра А. Параметр B
принимает значение, численно равное
корню нелинейного уравнения
при заданных изменениях значений
аргумента X
и параметра A,
начальном значениях параметра A,с
шагом Da,
конечном значении параметра A
числе значений аргумента X
и параметра А. Параметр B
принимает значение, численно равное
корню нелинейного уравнения
 .
.
Анализ задания
Входные данные:
N – количество значений параметра А, тип – целый;
An – начальное значение параметра А, тип – вещественный;
Da – шаг изменения значений параметра A, тип – вещественный;
D – верхняя граница значения изоляции корня, тип – вещественный;
C – нижняя граница значения изоляции корня, тип – вещественный;
Eps – погрешность вычисления интеграла, тип – вещественный;
Km – предельное число повторений цикла, тип – целый.
Выходные данные:
Mx – массив значений аргумента X, тип – вещественный;
Ма – массив значений параметра A, тип – вещественный;
My – двумерный массив значений функции Y, тип – вещественный;
Er – двумерный массив признака ошибки, тип – вещественный;
В алгоритме выполняются следующие функции:
Ввод исходных данных;
Вычисление значения параметров функции;
Вычисление значения определенного интеграла;
Вывод значения параметра функции;
Вычисление таблицы значений функции;
Проверка значения аргумента и формирование признака ошибки, если он имеет неположительное значение;
Вывод результатов вычислений.
Теоретические сведения
Нелинейное уравнение, метод половинного деления .
Схемы алгоритмов
Условие |
Алгоритм |
Значение |
X |
X |
Аргумент функции, вещественный тип |
|
Mx |
Массив значений аргумента X, вещественный тип |
An |
An |
Начальное значение параметра А, вещественный тип |
Da |
Da |
Шаг изменения значений параметра A, вещественный тип |
N |
N |
Количество значений параметра А, целый тип |
M |
M |
Количество значений аргумента Х, целый тип |
Ма |
Ма |
Массив значений параметра A, вещественный тип |
B |
B |
Параметр функции, вещественный тип |
Y |
Y |
Функция, вещественный тип |
|
My |
Двумерный массив значений функции, вещественный тип |
|
Er |
Двумерный массив признака ошибки, целый тип |
|
i |
Счётчик повторения цикла, целый тип |
|
j |
Счётчик повторения цикла, целый тип |
a |
C |
Нижняя граница значения изоляции корня, вещественный тип |
b |
D |
Верхняя граница значения изоляции корня, вещественный тип |
|
Km |
Предельное число повторений цикла, тип – целый |
ε |
Eps |
Погрешность вычисления интеграла, тип – вещественный |
|
Z |
Численное значение интеграла, вещественный тип |
|
Err |
Признак ошибки при вычислении интеграла, целый тип |

Схема алгоритма главной программы.