ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ И ГАЗОВЫЙ РАЗРЯД

Газовый разряд — это процесс протекания электрического тока через газ. Различают несамостоятельные и самостоятельные разря­ды. Несамостоятельный разряд возможен при инжекции электронов в раз­рядный промежуток (например, термоэмиссия с катода) или при иониза­ции газа каким-либо внешним источником. Несамостоятельные разряды используют довольно широко: это и ионизационные камеры технологиче­ского и дозиметрического назначения на атомных реакторах, газотроны в выпрямительных установках сетей питания постоянным током, плазмотроны с накаливаемым катодом и т.д. Физические процессы, протекающие в разных несамостоятельных разрядах, естественно, различаются, но не все они характерны для собственно газовых разрядов, как обычно пони­мают этот термин. В них с помощью электрического поля просто собира­ют образующиеся в объеме заряды (что вообще-то не совсем «просто»!), в пропорциональных счетчиках используют ограниченное образование электронных лавин, в гейгеровских счетчиках происходит коронный раз­ряд, в газотронах и тиратронах «обходят» закон «3/2», как бы приближая анод к катоду, в дуговых лампах дневного света термоэмиссия с подогревных катодов только обеспечивает зажигание самостоятельной дуги. Однако наиболее широко применяются самостоятельные разряды, о них и будет речь. Самостоятельный тлеющий разряд зажигается тогда, когда напряжение на его активных участках достигает «напряжения про­боя», для дугового разряда необходимо создать условия возникновения термоэмиссии с катода. Коронные разряды возникают только при наличии участков с очень большой неоднородностью напряженности электриче­ского поля, а искровые разряды принципиально импульсные. Все это справедливо для постоянных электрических полей, у полей ВЧ и СВЧ, которые широко используются в технологиях, есть своя специфика, осо­бенно у полей лазерной искры.

Электрический ток в газах

Столкновения частиц могут иметь упругий и неупругий характер. При упругом столкновении меняется направление движения частиц, про­исходит обмен импульсами и кинетической энергией. При неупругом столкновении внутренняя энергия и состояние одной из частиц (редко ко­гда обеих) изменяется. Ионизация атома при ударе электроном происхо­дит за счет передачи кинетической энергии электрона атому. Значение энергии электрона, достаточное для ионизации атома называется потен­циалом ионизации U_i . При многократной ионизации энергия, необходимая для отрыва каждого следующего электрона возрастает. Пионерами экспе­риментального определения потенциала ионизации атомов были Франк и Герц. Метод определения основывался на том, что зависимость тока, про­текающего через диод в парах ртути, от ускоряющего электроны напря­жения носит не монотонный возрастающий характер, а имеет провалы из-за потерь энергии электронов на возбуждение и ионизацию атомов ртути. Зависимость вероятности ионизации атомов любого газа f_i от энергии час­тиц U функцией ионизации:

f_i = а (U - U_i ) exp( - (U - U_i )/b), (1)

где а и b — эмпирические константы для конкретного газа.

Время между столкновениями, приводящими к ионизации, обратно пропорционально частоте ионизации _i = 1/_i,. Число ионизации в единицу времени пропор­ционально плотности частиц газа п, скорости налетающей частицы v и сечению ионизации _i:

_i = n_i. (.2)

Ионизационный пробег _i (длина, на которой частица может ионизовать) равен

(3)

где Si = n_i называется суммарным сечением ионизации. Суммарное сече­ние ионизации так же хорошо аппроксимируется подобной (8.1) зависи­мостью от энергии частицы U:

(4)

(формула Моргулиса)

где а и b — эмпирические константы для конкретного газа.

Зависимость суммарного сечения возбуждения имеет похожий вид:

(5)

(формула Фабриканта),

где U_r - потенциал возбужденного уровня, U_шах и S _max - энергия и сечение возбуждения в максимуме функции возбуждения, значения которых мож­но найти в справочных таблицах для конкретного газа. Время пребывания атома в возбужденном состоянии можно связать с числом переходов в единице объема в единицу времени N, тогда за промежуток времени dt число переходов: Ndt = wn_adt, где w — вероятность данного перехода, n_a — концентрация возбужденных атомов. Число актов излучения равно убыли числа возбужденных атомов: Ndt = - dn_a, тогда dn_a= - wn_adt. Таким обра­зом, число возбужденных атомов изменяется во времени по закону:

n_a(t) = n_a0exp(-wt), (6)

где n_a0 — концентрация возбужденных атомов в начальный момент време­ни. За время t_o = l/w концентрация уменьшается в «е» раз. Это время и полагают временем пребывания атома в возбужденном состоянии. Не­смотря на малость этой величины t_o ~ 10^-8 — 10^-7 с, даже за столь короткое время существования возбужденного атома возможно получение новой порции энергии, достаточной для перехода атома на следующий уровень возбуждения, либо для ионизации атома, в этом случае говорят о ступен­чатой ионизации. Именно такой процесс ступенчатой ионизации атомов ртути наблюдался в опытах Франка и Герца. Среди возбужденных со­стояний атомов и молекул существуют метастабилъные состояния, вре­мена жизни которых от 10^-4 до нескольких секунд. Самый нижний метастабильный уровень называется резонансным. Для ртути резонансный уровень возбуждения равен 4.7 эВ, при превышении энергией электронов этого значения наблюдался первый провал в зависимости тока от уско­ряющего электроны потенциала. Метастабильная частица при столкнове­нии с электроном может и дезактивироваться, т.е. перейти в основ­ное состояние, этот процесс называется неупругим соударением вто­рого рода.

Кроме образования положительных ионов при протекании тока в газе возможно возникновение отрицательных ионов. Для того, чтобы от­рицательный ион существовал и был устойчив, его внутренняя энергия Е_i, должна быть меньше, чем энергия нормального состояния пары атом — свободный электрон Е₀ Разность А = Е₀ - Е_i называется сродством атома к электрону. В атомах с заполненной внешней электронной оболочкой (инертные газы Не, Ne, Ar, Хе, Кг,...) электронная оболочка экранирует ядро и вероятность образования отрицательных ионов мала. Атомы с не­полными внешними оболочками (F, Cl, К, Na...), у которых оболочки ближе всего к заполнению, образуют наиболее устойчивые отрицательные ионы. Сродство этих атомов достаточно велико: А_F- = 3.43.6 эВ, А_Cl- = 3.82 эВ. Если электрон до столкновения имел кинетическую энер­гию E_к , то при его захвате должна освобождаться энергия А + E_к . Эта энергия может освобождаться через излучение: е + а —> а^- + hy, но более вероятен процесс образования отрицательного иона в результате столкно­вения трех тел Х+ Y+ е —> Х ^- + Y + е или Х+ Y+ e —> Х + Y ^- .

Для описания электрического тока в газах недостаточно рассмот­рения процессов ионизации и рекомбинации. Необходимо описание дви­жения заряженных частиц под действием электрических и магнитных по­лей, причем статистическое, т. е. усредненное по многочисленным столк­новениям. При наличии электрического поля на хаотическое движение частиц накладывается направленное движение вдоль поля. Для стацио­нарного процесса распространения тока средняя энергия и средняя ско­рость электронов должны оставаться постоянными, несмотря на присутст­вие ускоряющего электрического поля. Это возможно, если электрическая сила компенсируется силой трения (электроны при столкновениях отдают часть своей энергии). Таким образом, средняя скорость движения от одно­го электрода к другому, которую называют скоростью дрейфа и_d , остается постоянной. Отношение скорости направленного движения (скорости дрейфа) заряженной частицы к напряженности электрического поля назы­вается подвижностью:

(7)

Скорость дрейфа можно оценить из предположения, что она много мень­ше тепловой скорости и в результате столкновения частица теряет всю

кинетическую энергию. За время между столкновениями _ст заряженная частица пройдет путь

тогда:

(8)

где — средняя длина свободного пробега, — тепловая скорость.

Для распределения Максвелла, усредненная по скоростям скорость дрей­фа (формула Ланжевена):

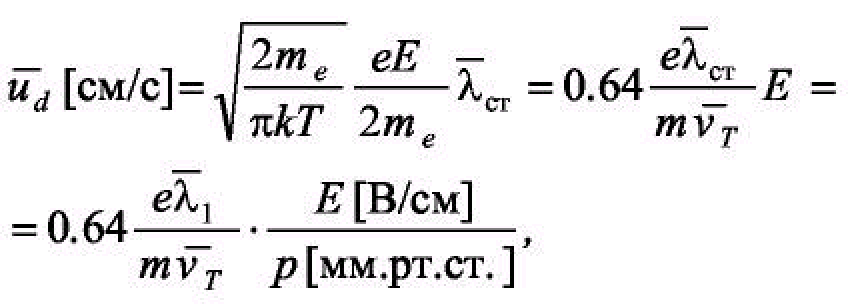( 9)

где - средний пробег при давлении 1 мм.рт.ст.

Для средней скорости дрейфа ионов формула Ланжевена имеет вид:

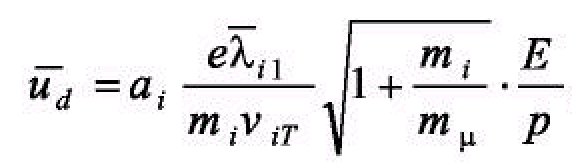(10)

где а_i - коэффициент, равный 0.5 1, т_ - масса молекулы иона.

Электроны на своем пути ионизуют атомы, «ионизующую» спо­собность электронов англичанин Таунсенд предложил характеризовать коэффициентом , названным впоследствии первым коэффициентом Таунсенда, равным числу электронов, создаваемых электроном на единице длины пробега. При таком описании прирост количества электронов про­порционален  и количеству атомов п: dn(x) = ndх. Тогда число электронов на расстоянии х:

n_e(х)= n₀ ехр(х), (11)

 - первый коэффициент Таунсенда:

=(1/n)(dn/dx). (12)

Процесс возникновения электронов можно также характеризовать часто­той ионизации Y_i — числом электронов, создаваемых одним электроном в единицу времени:

(13)

Тогда частота ионизации связана с первым коэффициентом Таун­сенда через скорость дрейфа:

.

Все три величины , Y_i , u_d зависят от напряженности электрического поля Е. Сразу отметим, что U(E), Y,{E), и_d(Е) весьма сложные зависимости, ме­няются с изменением условий разряда, но для Y_i(е) и (E) всегда весьма сильные (экспоненциальные, степенные).