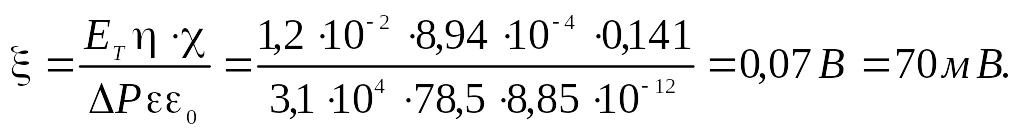Применение электрофореза и электроосмоcа

Наименование

Цель применения

Электрофорез Электроосмос

Нанесение покрытий; разделение и извлечение компонентов коллоидного раствора, масляных эмульсий и белков; очистка глины; извлечение мелких частиц из раствора, не поддающегося фильтрации Удаление избыточной влаги из капиллярно-пористых тел; дубление кожи; очистка дисперсионной среды коллоидных растворов, а также воды, глицерина, сахарных сиропов, желатина и др., в электрокинетических датчиках, преобразователях, усилителях и др. приборах

В пищевой промышленности, например, электрофорез применяют для очистки хлопкового масла. Напряженность внешнего электрического поля для его осуществления должна составлять —6,1∙10^–7 В/м. Знак «минус» показывает, что частицы загрязнений несут положительный заряд. Электроосмос используют для обезвоживания пищевых масс. Так, согласно существующей технологии скорость движения воды в сахаросодержащих коллоидных растворах составляет около 0,03 м/с.

7.4. Электрофоретическая подвижность

Все электрокинетические явления связаны с относительным перемещением дисперсной фазы и дисперсионной среды, осуществляемой по границе скольжения. Их интенсивность определяется значением ζ-потенциала. Поэтому данную величину используют для оценки электрокинетических явлений.

Двойной электрический слой можно рассматривать в качестве своеобразного конденсатора (рис. 7.9). Относительность движения дисперсной фазы и дисперсионной среды определяется силами f₁ и f₂. Сила f₁ возникает в результате взаимодействия избытка зарядов потенциалобразующего слоя по отношению к адсорбционному слою; она характеризует заряд диффузного слоя и направлена параллельно границе скольжения (линия АА), противодействуя силе трения. Сила f₁ определяется по формуле

f₁ = Eq_B, (7.9)

где Е — напряженность или градиент внешнего поля; q_B — плотность заряда поверхности.

Сила f₂ определяет трение жидкости при ее перемещении:

f₂ = h(ω/h), (7.10)

где h — коэффициент трения; ω — скорость движения жидкости; h — расстояние между поверхностями (см. рис. 7.9).

При установившемся движении эти силы равны, т.е.

Eq_B = η(v/h), или v = (q_Bh/η)E. (7.11)

Формула (7.11) определяет скорость взаимного перемещения дисперсной фазы и дисперсионной среды. Удельный заряд q_В можно связать с φ-потенциалом:

ζ = q_Bh/ε_а ; q_B = (ε_а/h)ζ, (7.12)

где ε_а — абсолютная диэлектрическая проницаемость.

Подставляя равенство (7.12) в формулу (7.11), получим

v = (ε_аζ/η)Е. (7.13)

Скорость движения в расчете на единицу напряженности электрического поля называют электрофоретической подвижностью, которая определяется по формуле

v_Е = v/Е = ε_аζ/η. (7.14)

С учетом формы частиц дисперсной фазы уравнения (7.13) и 7.14) принимают следующий вид:

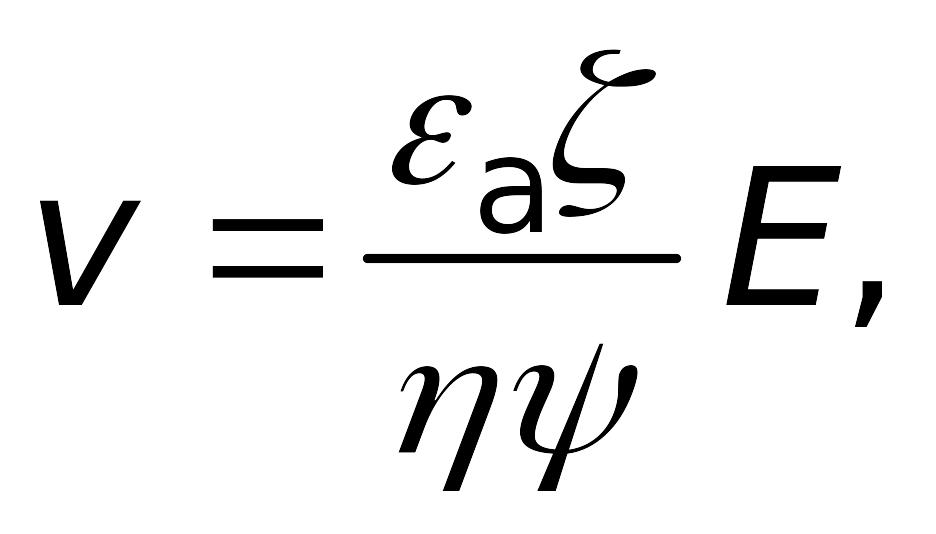(7.15) 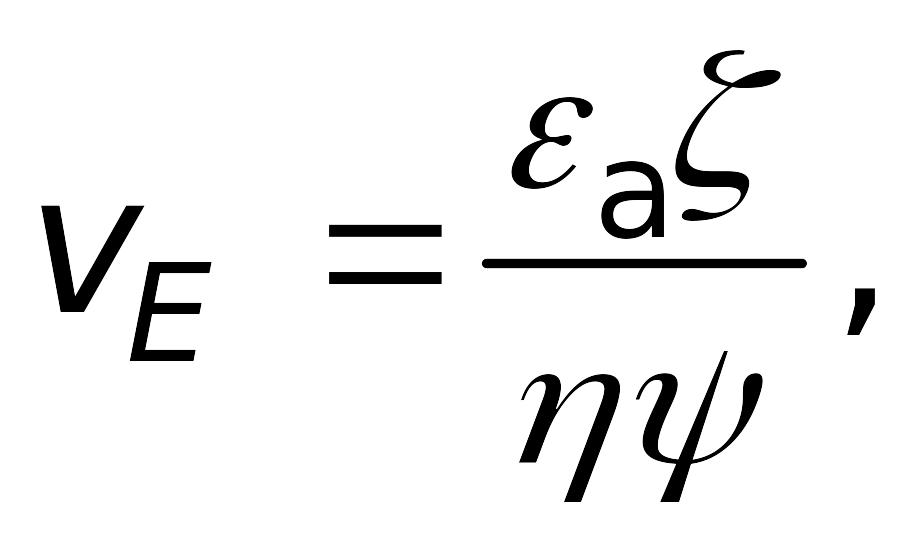(7.16)

где v — скорость, м/с; v_E — электрофоретическая подвижность, м²/с ∙ В, Ψ — коэффициент, зависящий от формы частиц; ζ — дзета-потенциал, В; Е — напряженность или градиент внешнего электрического поля, В/м.

Коэффициент Ψ учитывает форму частиц и их ориентацию в электрическом поле. Для шарообразных частиц коэффициент Ψ равен 0,66, а для цилиндрических, ориентированных вдоль силовых линий электрического поля — 1.

Абсолютная диэлектрическая проницаемость среды ε_а = ε ∙ ε₀, где ε — относительная диэлектрическая проницаемость; ε₀ — абсолютная диэлектрическая проницаемость вакуума, или электрическая постоянная, равная 8,85∙10^—12 K²/H∙м² (8,85∙10^—12 Ф/м).

С учетом значения абсолютной диэлектрической проницаемости формулу (7.15) можно представить в виде

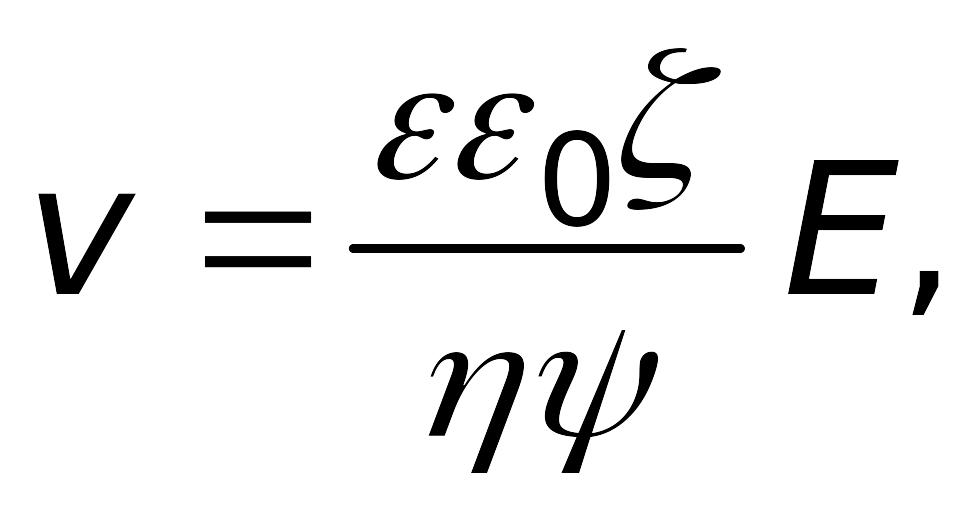или 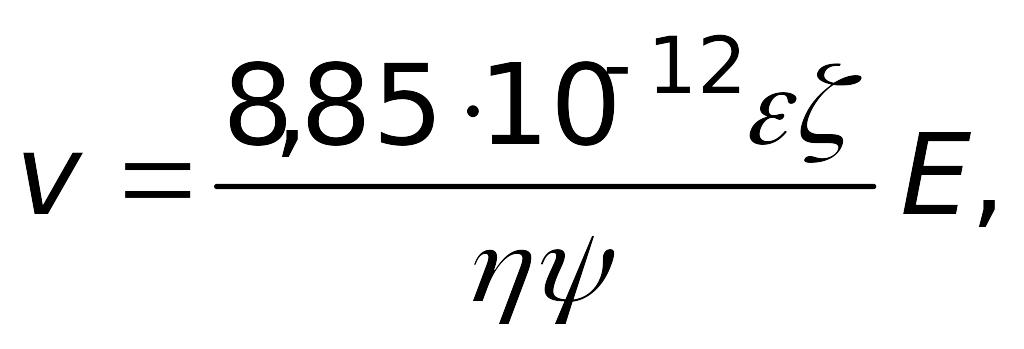(7.17)

Согласно формуле (7.17) величины, которые определяют интенсивность электрофореза и электроосмоса, зависят от свойств среды (η, ε), формы частиц (Ψ), напряженности внешнего электрического поля (Е) и электрокинетического потенциала (ζ), определяемого структурой ДЭС.

Электрофоретическую подвижность и электрокинетический потенциал довольно просто определить экспериментально по скорости перемещения дисперсной фазы; электрофоретическая подвижность обычно не превышает 5,0∙10^—8 м²/с∙В, а электрокинетический потенциал — 100 мВ.

В формулах (7.15) и (7.17) не учитывается ряд особенностей дисперсных систем, например электропроводность частиц дисперсной фазы, специфические свойства дисперсной системы в случае ее нахождения в щелях, каналах и капиллярах. Тем не менее, эти формулы являются основными для количественной характеристики электрокинетических явлений.

Для расчета потенциала течения Е_т который осуществляется под внешним воздействием Р₁ (см. рис. 7.8), можно воспользоваться следующей формулой:

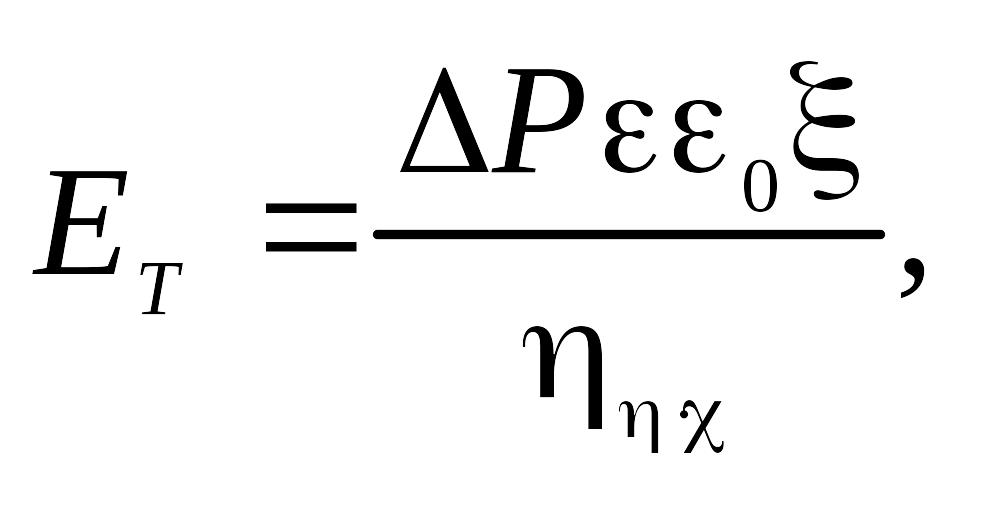(7.18)

где ΔР = Р₁ — Р₂ — перепад давления при течении дисперсионной среды; χ — удельная электропроводность дисперсионной среды.

Заметим, что потенциал течения возникает на любой границе раздела фаз при перемещении дисперсной фазы или дисперсионной среды. Так, например, кровь организма человека является дисперсной системой. Сердце, как своеобразный насос, заставляет кровь двигаться по сосудам. Потенциал течения крови составляет примерно 1—2 мВ, т.е. незначителен. При движении нефти по трубопроводам потенциал течения намного выше и может привести к электрическому пробою, пожару или взрыву. По той же причине наливать бензин в полиэтиленовую емкость крайне опасно, так как при опорожнении канистры возникает потенциал течения, который может вызвать искру и воспламенить бензин.

Таким образом, электрокинетические явления и электрофоретическую подвижность можно рассматривать как следствие образования ДЭС на границе раздела фаз. Возможность и интенсивность относительного перемещения фаз определяется величиной z-потенциала, которая обусловлена структурой ДЭС.

Упражнения

1. Электрокинетический потенциал высокодисперсных частиц золя апельсинового сока равен 50 мВ. Определите скорость электрофореза и электрофоретическую подвижность частиц золя сферической формы, если относительная диэлектрическая проницаемость среды e равна 54,8, внешняя ЭДС — 120 В, расстояние между электродами h = 40 см, вязкость среды η= 4,5∙10^—3 Па ∙ с.

В соответствии с формулой (7.17) при Е = E₁ /h

2. Определите электрокинетический потенциал коллоидов 20%-го раствора сахарозы при градиенте внешнего электрического поля 400 В/м, относительной диэлектрической проницаемости ε = 69,1, вязкости η = 2,5∙10^—3 Па ∙ с и скорости электрофореза v = 13.5 мкм/с.

По формуле (7.17) находим

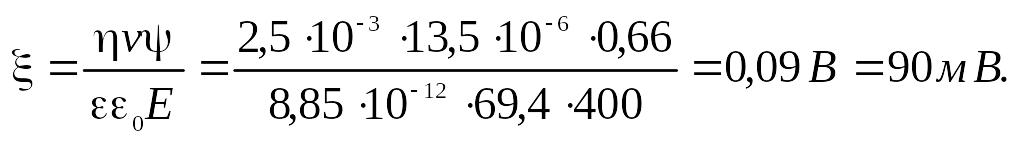
3. Найдите значения потенциала течения, если через мембрану продавливается 42,4%-й раствор спирта при следующих условиях: ΔР = 20∙10^—3 Па, удельная электропроводность χ = 1,3∙ 10^—3 См ∙ м^—1, относительная диэлектрическая проницаемость ε = 41,3, вязкость η = 0,9∙10^—3 Па∙с, электрокинетический потенциал ζ = 6∙10^—3 В.

Согласно формуле (7.18)

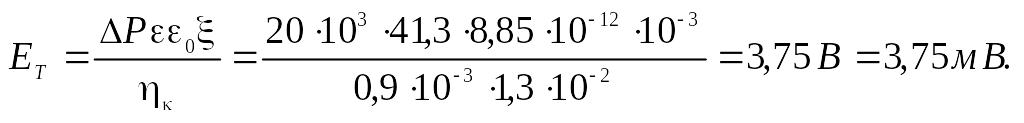
4. Чему равен электрокинетический потенциал при протекании 0,01 М раствора КСl через керамический фильтр под избыточным давлением (ΔР) 3,1∙10⁴ Па и потенциале течения Е_т = 1,2∙10^—2 В. При 298 К вязкость раствора η = 8,94∙10^—4 Па∙с, удельная электропроводность χ = 0.141 См∙м^—1, относительная диэлектрическая проницаемость ε = 78,5.

Из формулы (7.18) получаем