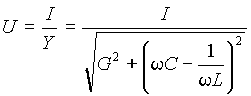18. Выражения для тока и падений напряжения для резонанса напряжений.

19. Сущность резонанса. Резонанс токов. Условия резонанса. Резонансные кривые.

Резона́нс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы.

Резонанс токов — резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.

Условия получения резонанса токов такие же, как и для резонанса напряжений: f =fo или xL = хC.

Резонансные кривые определяют, наблюдая изменение амплитуды вынужденных колебаний либо при медленной перестройке частоты p вынуждающей силы, либо при медленном изменении собственной частоты w₀.

20. Выражения для токов и падений напряжения для резонанса токов.

Резонанс токов, или параллельный резонанс, получается в случае, когда генератор нагружен на индуктивность и емкость, соединенные параллельно, т.е. когда генератор включен вне контура Условия получения резонанса токов такие же, как и для резонанса напряжений: f =fo или xL = хC.

При   резонансе   токов  действующие значения  токов  в каждом разветвлении, определяемые отношениями IL = U / XL  и  IC = U / XC будут  равны  между собой, так XL = ХC.

Такая цепь содержит два сложных потенциальных узла, а все элементы находятся под одним и тем же напряжением

Для любого из узлов - 1 или 1’ справедлив первый закон Кирхгофа:

 

 

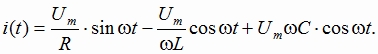
  Для параллельного соединения токи в отдельных элементах можно представить через проводимости  и  общее  падение   напряжения  U в виде

.

(16)

Пусть в режиме резонанса  падение   напряжения  на входе контура равно U₀, тогда токи в отдельных элементах будут

Падение   напряжения  на входе контура U при питании его от источника, обладающего свойствами источника тока  и  формирующего  ток  с действующим значением I, будет равно

21. От каких величин зависит значение угла сдвига фаз между напряжением и током?

В цепи переменного тока с активным сопротивлением ток и напряжение совпадают по фазе и угол сдвига фаз равен нулю. Угол сдвига фаз между током и напряжением зависит от соотношения между активным и реактивным сопротивлениями, включенными в цепь. Увеличение активного сопротивления приводит к уменьшению угла сдвига фаз. Реактивная нагрузка, подключенная в цепь, наоборот, увеличивает угол сдвига фаз. Под сдвигом фаз тока относительно напряжения подразумевается разность начальных фаз напряжения и тока, то есть ϕ =ψ –ψ

В общем случае, когда участок цепи содержит не только активное, но и реактивное (емкостное, индуктивное или и то и другое) сопротивление, напряжение между концами этого участка сдвинуто по фазе относительно тока, причем сдвиг фаз лежит в пределах от +p/2 до —p/2 и определяется соотношением между активным и реактивным сопротивлениями данного участка цепи.