9. Активная мощность в цепи переменного тока.

Активная мощность - количество электрической энергии, преобразованной в тепло. Для цепей переменного тока, когда ток и напряжение изменяются по синусоидальному закону с одинаковой частотой, она равна: P=UIcosφ

• Единица активной мощности - ватт (W, Вт).

10. Реактивная мощность индуктивности и емкости.

Реактивная мощность обусловлена способностью реактивных элементов накапливать и отдавать электрическую или магнитную энергию.

Eмкостная нагрузка в цепи переменного тока за время половины периода накапливает заряд в обкладках конденсаторов и отдаёт его обратно в источник. Индуктивная нагрузка накапливает магнитную энергию в катушках и возвращает её в источник питания в виде электрической энергии. Напряжение на выводах реактивного элемента будет достигать максимального значения во время смены направления тока, следовательно, расхождение во времени между напряжением и током в пределах элемента составит четверть периода (сдвиг фаз 90°).

Угол сдвига фаз φ в цепи нагрузки определяется соотношением реактивного и активного сопротивлений нагрузки.

Реактивная мощность характеризует потери, созданные реактивными элементами в цепи переменного тока, и выражается формулой Q = UIsinφ.

11. Полная мощность.

12. Полная мощность в комплексной форме.

Комплексное значение полной мощности, отражающее реальные мощности в цепи, получится, если умножить комплексное значение напряжения на сопряженное комплексное значение тока:

S = UI*.

Сопряженное комплексное значение тока I* отличается от I знаком перед мнимой частью. Если комплексное значение тока I = е в степени (jψ), то сопряженное ему комплексное значение I* = Iев степени (-jψ).

Покажем, что комплексное значение мощности отражает реальные мощности в цепи.

Допустим, что комплексные значения напряжения и тока какой-то цепи имеют выражения

U = Ue в степени (jψ1); I = Ie в степени (jψ2)..

Комплексное значение полной мощности

Выразив комплексное значение полной мощности в тригонометрической, а затем в алгебраической форме, получим

S = S cos φ + jS sin φ = Р + jQ,

где S cos φ = P — активная мощность цепи; S sin φ = Q — реактивная мощность цепи;

S = √р2 +Q2 — полная мощность.

Следует отметить, что при активно-индуктивном характере нагрузки (ψ1 > ψ2) знак перед jQ положительный, при активно-емкостном (ψ2 > ψ1) — отрицательный.

13.Треугольник сопротивлений и мощностей.

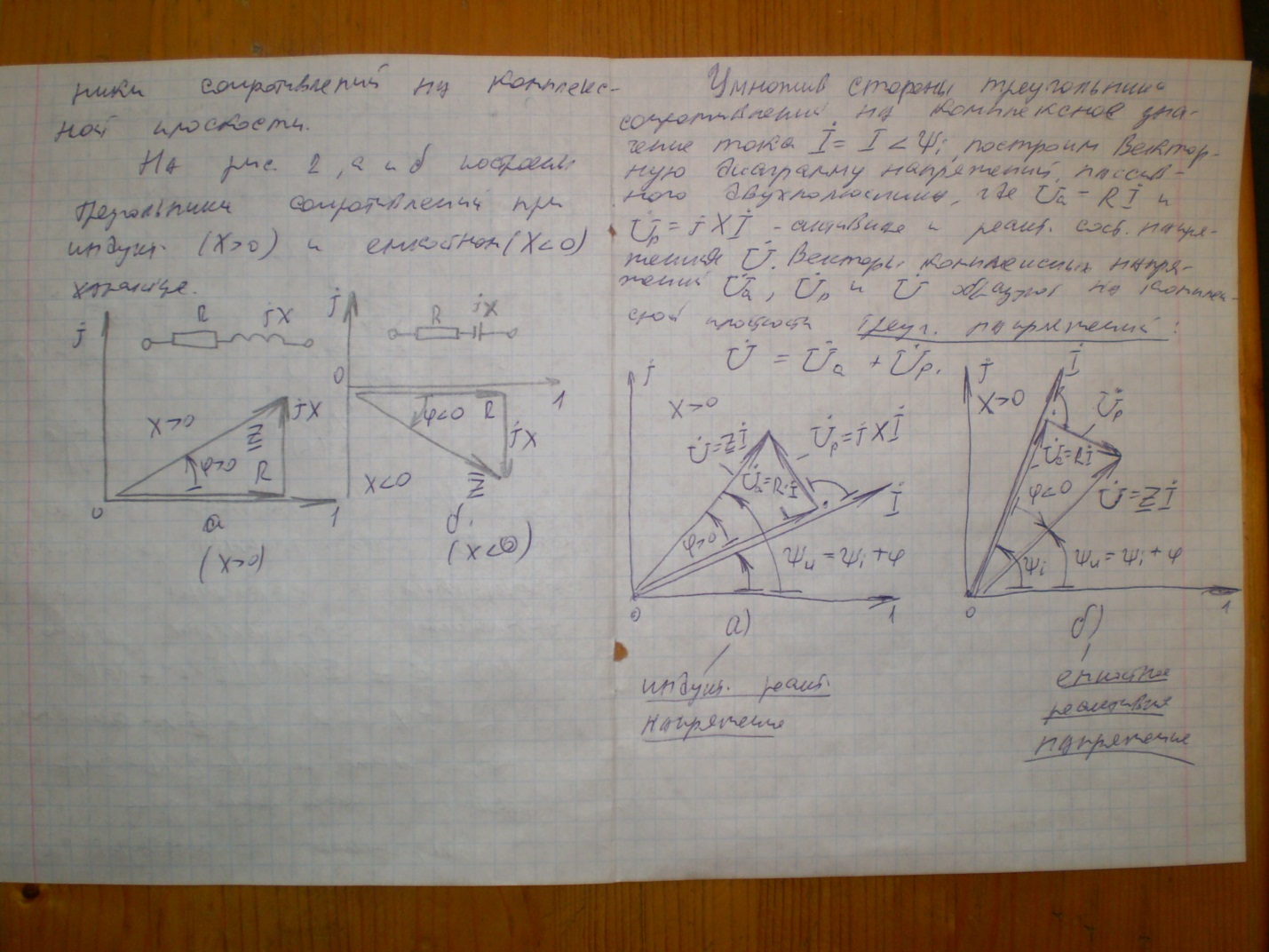
14. 1 И 2 законы Кирхгофа в комплексной форме.

 По первому закону Кирхгофа,  алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю:

 Равенство не нарушится, если вместо токов подставить соответствующие комплексы.  Это и будет выражение для первого закона  Кирхгофа  в комплексной форме:

  где  - количество ветвей, подходящих к узлу.

По второму закону Кирхгофа,  в любом (замкнутом) контуре справедливо равенство алгебраических сумм мгновенных значений  напряжений  на сопротивлениях контура и ЭДС:

  Заменив напряжения  и  ЭДС на соответствующие комплексы,  получим выражение для второго закона Кирхгофа в комплексной форме:

 где   - количество элементов в контуре,

            - количество ЭДС в контуре.

 Пример: