5 . Зависимость между током и напряжением для резистивного элемента. Закон Ома в комплексной форме. Векторная диаграмма. Фазовый сдвиг между током и напряжением.

Резистивным называют идеализированный двухполюсный элемент,

для которого связь между напряжением и током можно представить в виде

графика, называемого вольт-амперной характеристикой. Резистивный эле-

мент моделирует процесс необратимого преобразования электромагнитной

энергии в тепло и другие виды энергии, при этом запасание энергии в элек-

тромагнитном поле отсутствует.

Закон Ома в комплексной форме:

I = U/Z,

где Z = r + jx_L для цепи, состоящей из последовательно включенных активного r и индуктивного x_L сопротивлений; Z = r -- jx_C для цепи, состоящей из последовательно включенных активного r и емкостного х_C сопротивлений.

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов.

Гармоническое (то есть синусоидальное) колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постоянной угловой скоростью ω. Длина вектора соответствует амплитуде, угол поворота относительно оси (Ox) - фазе.

вариант построения векторной диаграммы (для последовательно соединенных резистора, индуктивности и конденсатора) приведен на рисунке.

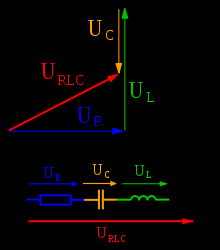
фазовый сдвиг φ между напряжением и током равен разности начальных фаз напряжения и тока, т.е.

φ = ψ_u -ψ_i .

Если φ >0, то напряжение опережает по фазе ток; если φ <0, то напряжение отстает по фазе от тока (или ток опережает напряжение); если φ =0, то напряжение совпадает по фазе с током.

6 .Зависимость между током и напряжением для индуктивного элемента. Закон Ома в комплексной форме. Векторная диаграмма. Фазовый сдвиг между током и напряжением.

7. Зависимость между током и напряжением для емкостного элемента. Закон Ома в комплексной форме. Векторная диаграмма. Фазовый сдвиг между током и напряжением.

Связь между током и напряжением на емкостном элементе  . 

Закон Ома в комплексной форме получаем из формулы для комплексного сопротивления:  Применение векторных диаграмм при расчете и исследовании электрических цепей переменного тока позволяет наглядно представлять рассматриваемые процессы и упрощать производимые электротехнические расчеты.

Векторные диаграммы являются совокупностью векторов, изображающих действующие синусоидальные ЭДС и токи или их амплитудные значения.

Гармонически изменяющееся напряжение определяется выражением u = U_m sin (ωt + ψ_и).

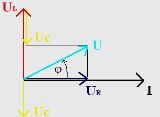
Угол фазового сдвига между током и напряжением равен .

8. Основы символического метода расчета цепей переменного тока. Комплексное сопротивление и комплексная проводимость.

Метод расчёта цепи, основанный на применении комплексных чисел, называется символическим методом. В символическом методе расчета все реальные параметры электрической цепи заменяют символами в комплексной форме записи. После замены реальных параметров цепи на их комплексные символы расчет цепей переменного тока выполняют методами, которые применяли для расчета цепей постоянного тока. Отличие состоит в том, что все математические операции необходимо выполнять с комплексными числами.

В результате расчета электрической цепи искомые токи и напряжения получаются в виде комплексных чисел. Завершают расчёт цепи переменного тока, как правило, составлением баланса активных и реактивных мощностей, который позволяет проверить правильность вычислений.

Комплексной проводимостью называется отношение комплексного тока к комплексному напряжению

Y=I/U=1/Z=1/(zejj)=ye‑jj=yÐ‑j,  (6.31а)

 где y=1/z — величина, обратная полному сопротивлению, называется полной проводимостью.

Комплексная проводимость и комплексное сопротивление взаимно обратны. Комплексную проводимость можно представить в виде

 Y= ye‑jj=ycosj‑jysinj=g‑jb, (6.31б)

 где g=ycosj — действительная часть комплексной проводимости, называется активной проводимостью; b=ysinj — значение мнимой части комплексной проводимости, называется реактивной проводимостью;