7. Визначення діапазону зміни параметра к за методом д-розбивки

Передаточна функція розімкнутої системи:

Характеристичний поліном замкнутої системи:

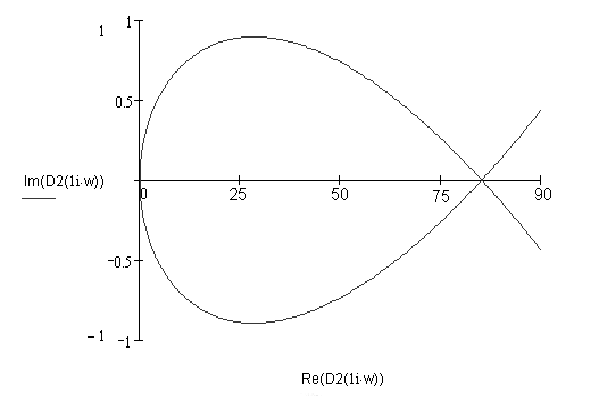
Рис.7 Межа розбиття за параметром К

Оскільки коефіцієнт К=21 входить в область допустимих коефіцієнтів, тому система нестійка

8. Визначення коефіцієнтів помилок сак

Усталена похибка при гармонічній вхідній дії має вигляд:

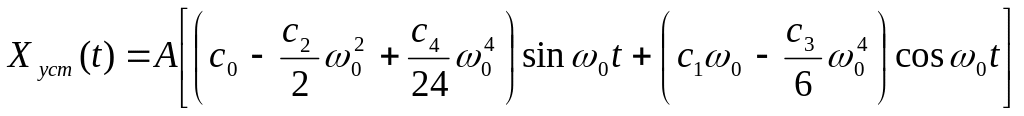
Ми розраховуємо три коефіцієнта похибок , , , бо вони мають фізичний зміст. Обчислимо їх шляхом поділу полінома чисельника передаточної функції за похибкою на поліном знаменника.

Отже коефіцієнти похибок дорівнюють:

= 0,045

= 0,326

= 0,039

Вхідний сигнал g(t)=1

X_уст=0,045 тому графік усталеної похибки матиме вигляд:

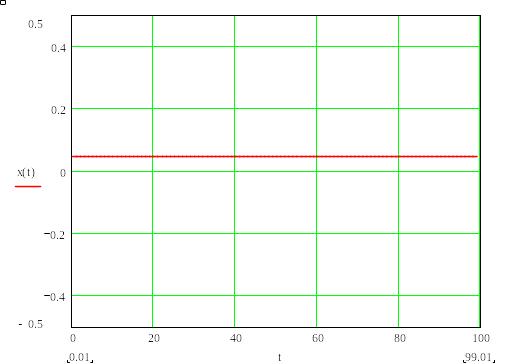
9. Побудова кривої перехідного процесу

Перехідною характеристикою називається графік зміни в часі вихідної величини ланки або системи, коли на вхід подається одиничний ступінчастий сигнал. Аналітичним виразом для перехідної характеристики є перехідна функція. Перехідною функцією називається аналітичний опис зміни вихідної величини у часі при впливі одиничного ступінчастого сигналу при нульових початкових умовах.

Передаточна функція замкненої системи:

Будуємо графік перхідної характеристики в програмному середовищі MatLab (рис.8)

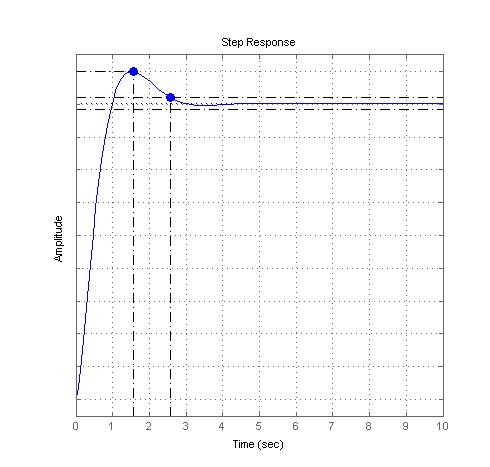
Рис. 8. Перехідний процес в системі при вхідній одиничній ступунчатій дії

За графіком перхідної характеристики оцінюємо якість САК:

Час перехідного процесу t_p=2,57 c.

Відносне перегулювання .

Як бачимо система досить швидко переходить до стабільного стану, а перерегулування становить 5 %.

Висновки

В розрахунково-графічній роботі було досліджено лінійну неперервну САК. Система виявилася стійкою за різними критеріями стійкості. Побудовано амплітудно-фазо-частотну характеристику розімкненої САК та визначено стійкість замкненої САК за критерієм Найквіста. Побудовано також логарифмічні частотні характеристики та по них визначено запаси стійкості системи. Отримано графік перехідної характеристики та визначено час перехідної характеристики та пере регулювання.

Література

1. Самотокін Б.Б. „Лекцій з теорії автоматичного керування”: Навчальний посібник для студентів вищих технічних закладів. Житомир: ЖІТІ, 2001– 503 с.

2. Довідкова система MathCAD Professional 2000.

3. Плечистий Д.Є. „Датчики” Житомир: ЖІТІ, 2001 – 355 с.

4. Інтернет мережа.

5. Довідкова система MatLab .