Завдання

1. Використовуючи правила структурних перетворень схем САК, одержати одноконтурну схему системи типу

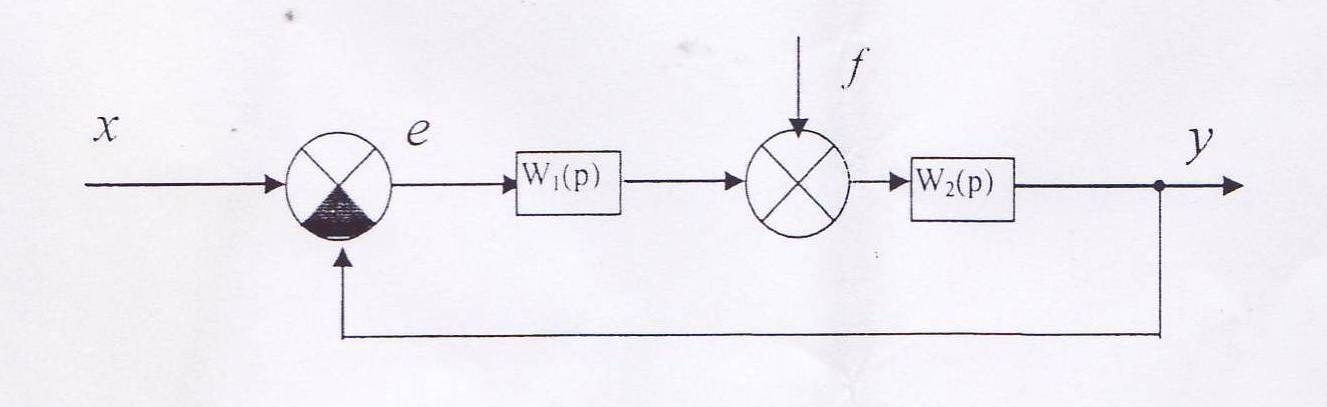
де: х- вхідна величина; f- сигнал збурення; y - вихідна величина; е - сигнал похибки.

2. Визначити передаточні функції: розімкнутої САК, замкнутої САК, за похибкою та по збуренню.

3. Дати визначення стійкості САК.

4. Визначити стійкість замкнутої САК за критеріями Рауса, Гурвиця та Михайлова.

5. Побудувати амплітудно-фазо-частотну характеристику розімкненої САК та визначити стійкість замкненої САК за критерієм Найквіста.

6. Побудувати логарифмічні частотні характеристики:

6.1. Амплітудно-частотну характеристику (ЛАЧХ);

6.2. Фазо-частотну характеристику (ЛФЧХ) розімкненої САК, по них визначити запаси стійкості системи.

3. За допомогою методу Д–розбивки визначити діапазон зміни заданого параметра (за варіантом).

4. Визначити коефіцієнт помилок САК С₀, С₁ С₂ та представити похибку в аналітичній формі.

5. Використовуючи спеціальні програми для ЕОМ побудувати криву перехідного процесу замкненої системи.

Система керування описується наступними рівняннями:

; ; ;

Вихідні дані
Варіант	, с	, с	, с
7	0,08	0,8	7	0,4	0,6	7	3

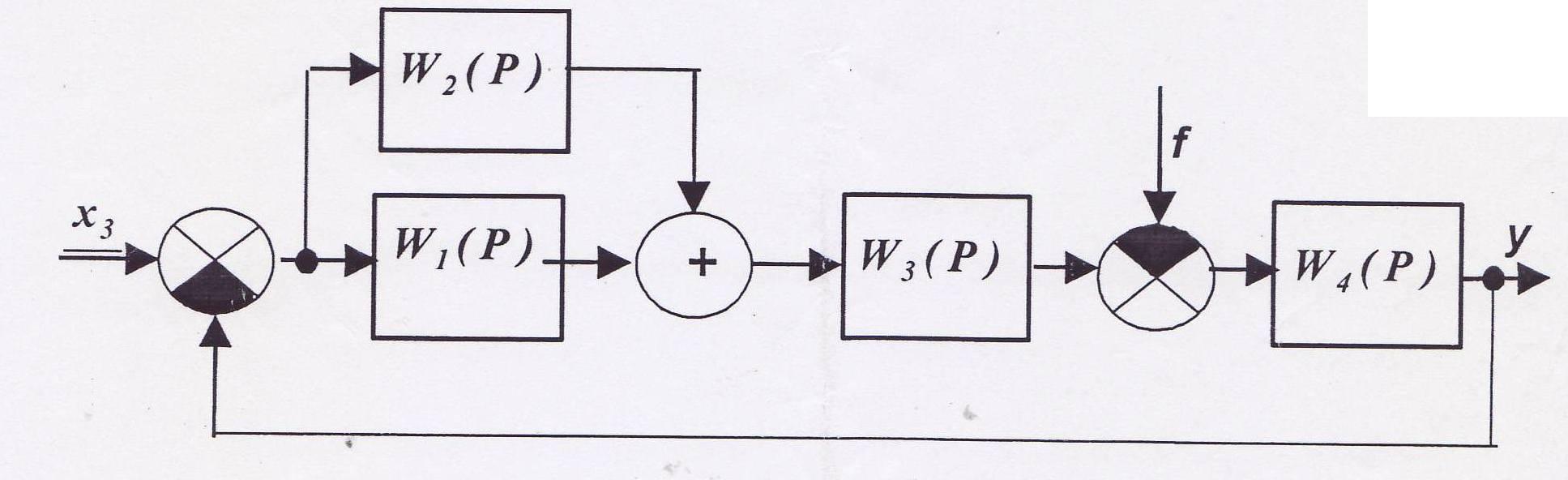
Рис. 1. Cтруктурна схема САК

1. Отримання одноконтурної САК

Використовуючи правила структурних перетворень схем САК, одержали одноконтурну систему (рис. 2), де: х- вхідна величина; f- сигнал збурення; y - вихідна величина.

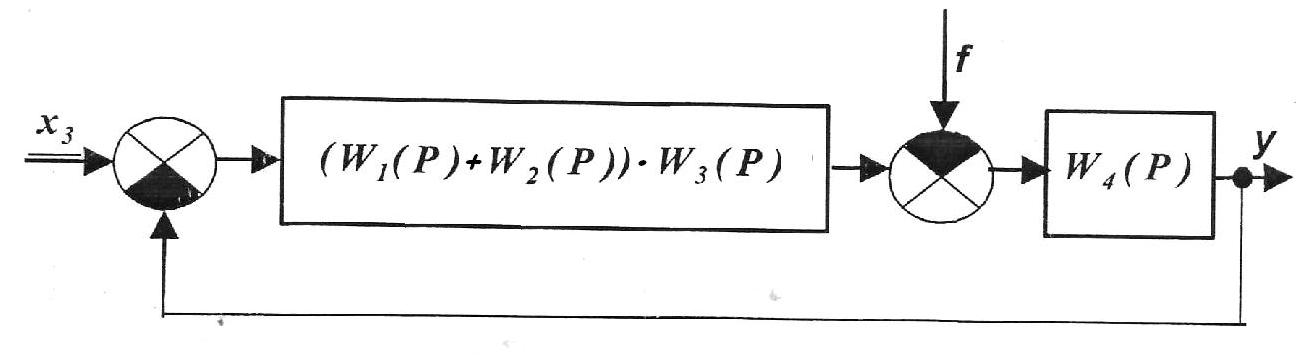
Рис. 2. Одноконтурна САК

2. Визначення передаточних функцій сак

2.1. Розімкнута САК:

2.2. Замкнута САК:

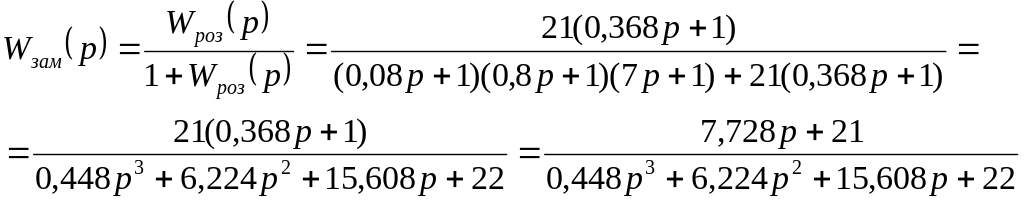
2.3. Передаточна функція системи за похибкою:

2.4. Передаточна функція системи по збуренню:

3. Визначення стійкості сак

Однією з найважливіших характеристик автоматичної системи керування є стійкість. Цим поняттям характеризується працездатність системи. Система, що не володіє стійкістю, не здатна виконувати функції керування і має нульову або навіть негативну ефективність (тобто система шкідлива).

Нестійка система може привести керований об'єкт до аварійного стану. Тому проблема стійкості систем є однією із центральних у теорії автоматичного керування.

Стійкість автоматичної системи - це властивість системи повертатися у вихідний стан рівноваги після припинення дії, яка вивела систему з цього стану.

Загальна умова стійкості: для стійкості лінійної автоматичної системи керування необхідно і достатньо, щоб дійсні частини всіх коренів характеристичного рівняння системи були від’ємними. При цьому дійсні корені розглядаються як окремий випадок комплексних, в яких мнима частина дорівнює нулю. Якщо хоча б один корінь має позитивну дійсну частину, то система буде нестійкою.

Стійкість системи залежить тільки від вигляду коренів характеристичного рівняння і не залежить від характеру зовнішніх впливів на систему. Стійкість є внутрішня властивість системи.

У теорії автоматичного керування розроблено ряд правил, за допомогою яких можна судити про знаки коренів, не вирішуючи характеристичне рівняння і не знаходячи числові значення самих коренів. Ці правила називаються критеріями стійкості. Найпростішим критерієм стійкості є умова позитивності коефіцієнтів характеристичного рівняння. Позитивність коефіцієнтів характеристичного рівняння є необхідною (але не достатньою) умовою стійкості системи. Це означає, що коли всі коефіцієнти позитивні, то система може бути стійкою або нестійкою. Але якщо хоча б один коефіцієнт негативний або дорівнює нулю, то система нестійка. Критерії стійкості можуть бути алгебраїчними і частотними. Алгебраїчні критерії встановлюють необхідні й достатні умови від’ємності коренів у формі обмежень, що накладаються на певні комбінації коефіцієнтів характеристичного рівняння. Частотні критерії визначають зв'язок між стійкістю системи і формою частотних характеристик системи.