2.8. Графическое представление отношений

Множества упорядоченных пар, входящие в отношения, сложно «расшифровываются», ненаглядны. Для изображения бинарных отношений на небольших множествах можно использовать графические представления.

Пусть А = {a, b, c, d} и отношение R = {a,b, a,c, b,d, c,e, e,b}.

 Метод представления, относящийся к традиционной аналитической геометрии: чертится пара взаимно перпендикулярных осей OX и OY и на каждой отмечаются точки, представляющие элементы множества A. Далее в правом верхнем координатном углу отмечаются точки с координатами (x, y), где x  A, y  A. Таким образом, для множеств R_I, R_U, R имеем:

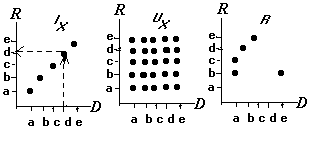
Недостаток: при увеличении |A| трудно увидеть элементы в области и установить соответствие с точками, обозначающими отношения.

 И, наконец, можно не дублировать одни и те же элементы, оставить стрелки, но позволить им изгибаться, изображение становится более наглядным:

2.9. Свойства отношений

Отношения могут обладать рядом свойств, которые определяются через условия, которым должны удовлетворять их элементы.

Итак, пусть  – отношение на множестве A. Тогда

a)  рефлексивно, если  x  A x x;

b)  симметрично, если x у х y y x;

c)  транзитивно, если x y и y z  x z;

d)  антисимметрично, если х y и ух  х= у.

Пример 2.12.

Пусть A — множество всех людей, а P и S – отношения на А, определяющиеся следующим образом:

Р = {x,y: x – предок y}

S = {x,y: x и y имеют общих родителей}

Тогда Р – транзитивно, а S — рефлексивно, симметрично и транзитивно. 

Пример 2.13.

Пусть N – множество натуральных чисел.

 = N, R;  = N, S;  = N\{1}, T.

R = {x,y: x – делитель y},

S = {x,y: x y},

T = {x,y: x и y имеют общий делитель}.

Тогда :

4. рефлексивно, т.к. x/x=1 для всех x N;

b) несимметрично, т.к., например, 2 — делитель 4, но 4 не является делителем 2;

c) транзитивно, т.к. если y/x  N и z/x N, то z/x=(y/x)*(z/y)  N;

d) антисимметрично, т.к. если y/x  N и x/y N, то x=y.

Аналогично :

4. рефлексивно, т.к. x  x для всех x N;

b) несимметрично, т.к., например, 2 3, но 3 не  2;

c) транзитивно, т.к. если x  y и y  z, то x  z;

d) антисимметрично, т.к. если x  y и y  x, то x=y.

Наконец, :

4. рефлексивно, т.к. x и x имеют общий делитель;

b) симметрично, т.к. если x и y имеют общий делитель, то y и x имеют общий делитель (тот же);

c) не транзитивно, т.к. например, 2 и 6 имеют общий делитель, 6 и 3 имеют общий делитель, но 2 и 3 не имеют общего делителя;

d) не антисимметрично, т.к. например, из того, что 2 и 6 имеют общий делитель, 6 и 2 имеют общий делитель, не следует, что 2=6. 

Заметим, что свойства симметричности и антисимметричности не являются взаимоисключающими. Действительно, для любого множества X отношение I_X является и симметричным, и антисимметричным. Можно также привести пример отношения, которое не является ни симметричным, ни антисимметричным.

Пример 2.14.

Пусть P – множество всех людей. Определим отношение B так, что xBy тогда и только тогда, когда x является братом y. В семье из двух братьев p и q и сестры r мы имеем ситуацию, изображенную на следующей диаграмме:

Отношение B не симметрично, т.к. pBr, но не rBp. Это отношение также и не антисимметрично, т.к. pBq и qBp имеют место, но p и q различны. 

В общем случае можно проинтерпретировать характеристики отношения через его диаграмму:

a) отношение рефлексивно – для каждого узла (точки) на диаграмме существует стрелка, которая начинается и заканчивается на этом узле;

b) отношение симметрично – для каждой стрелки, соединяющей два узла, существует также стрелка , соединяющая эти узлы в обратном направлении;

c) отношение транзитивно – для каждой пары узлов x и y, связанных последовательностью стрелок от x к a₁, от a₁ к a₂, ..., от a_n-₁ к a_n, от a_n к y, существует также стрелка от x к y.

d) отношение антисимметрично – не существует двух различных узлов, связанных парой стрелок.

Рассмотрим еще три свойства отношений: иррефлексивность, асимметричность и сравнимость.

Отношение  на множестве A иррефлексивно, если x

Отношение  асимметрично, если x y xy .

Отношение  сравнимо, если x y x y  y x.