2. Множества и отношения

2.1. Множества и их спецификации. Пустое и универсальное множества

Множество — совокупность определенных различаемых объектов таких, что для любого объекта можно установить, принадлежит этот объект данному множеству или нет.

Природа объектов произвольна, (например, множество натуральных чисел, множество станций кольцевой линии московского метро и т.д.); для большинства примеров используются абстрактные множества, например, множества чисел.

Множества обозначаются прописными буквами: A, B, C ..., элементы – строчными буквами: x, y, z, …

Множества задаются одним из двух способов:

1) перечислением всех элементов множества (A= {7, 8, 9})

2) указанием свойств элементов множества (A={x: x – целое число и 6 < x < 10})

Множества – неупорядоченные совокупности объектов, то есть {7,8,9}, {8,9,7} и {9,8,7} – разные виды записи одного и того же множества.

Принадлежность элемента х множеству А обозначается x  A. Если элемент х не принадлежит множеству А, это обозначается x  A.

Пример 2.1.

Какие из следующих множеств заданы правильно?

A = {1, 2, 3}; B = {5, 6, 6, 7}; C = {x: x  A}; D = {A, C}

Разъяснение:

A – правильно определено, т.к. число членов множества конечно и среди элементов нет повторений.

B –определено неправильно, т.к. содержит два одинаковых элемента.

C – правильно определено (так как правильно определено A), ибо если x A, то x C и если x  A, то x  C.

D – правильно определено, поскольку A и C представляют множества, то D – множество множеств. В множестве D только два элемента. В частности, 1  D, хотя 1 A и A D. Действительно, 1  A, 1  C  1D.

Пустое множество (обозначается ) есть множество, которому не принадлежит никакой элемент, то есть, множество, обладающее свойством

x х  .

Универсальное множество (обозначается E) есть множество всех рассматриваемых в данной задаче элементов. Оно обладает свойством

x х E .

2.2. Диаграммы Венна

Это одно из геометрических представлений множеств, оно полезно для иллюстраций, а также для проверки справедливости конкретного утверждения до его формального доказательства. Если же утверждение является неверным, то геометрическая иллюстрация облегчает построение контрпримера. Диаграммы Венна названы по имени английского математика Джона Венна, иногда их называют «диаграммы Эйлера – Венна».

В этих диаграммах прямоугольник изображает множество E, а круги (овалы, прямоугольники) – другие множества, являющиеся подмножествами E. Точки внутри фигур рассматриваются как элементы соответствующих множеств (иногда они прямо внутри фигур и записываются). Обычно области диаграммы Венна штрихуют для обозначения вновь образованных множеств.

Пример 2.2.

Пусть E = {b, c, d, e, f}, A = {b, c, d}, B = {c, e}. Соответствующей диаграммой будет:

А

В

(a)Е

b

d

c

e

f



3. Равенство множеств. Подмножества

Говорят, что множества A и B равны (запись: A = B), если они состоят из одних и тех же элементов. Формально это можно записать:

A = B  x х A  х B

. ^Df

Обозначение Df под знаком  означает эквивалентность по определению.

Множество A есть подмножество множества B, если из принадлежности x  A следует, что x  B (запись: A  B). Формально это можно записать:

A  B  x х A  х B

. ^Df

Если существует элемент B, который не принадлежит A, то A называют собственным подмножеством B (запись A  B).

Соответствующая диаграмма Венна такова:

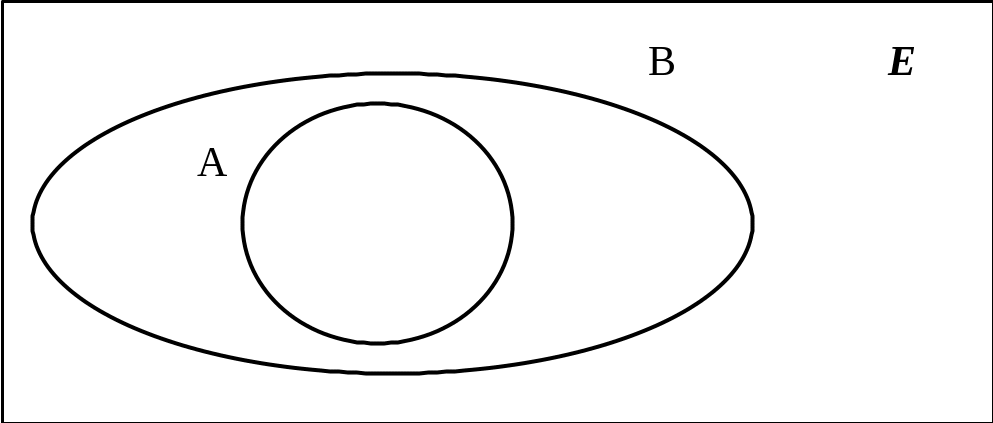
Если записать в обратном порядке: B  A (или B A), то говорят, что B – (собственное) надмножество A.

Очевидно, что для любого множества A   A, A  A, A  E.

Равенство множеств A и B означает, что все элементы A являются элементами B, а все элементы B – элементами A, то есть множества A и B равны, если A  B и B  A.

Это свойство формально можно записать так

A = B  A  B  B  A

Доказательство

Для доказательства воспользуемся методом принадлежности, основанным на формальных определениях равенства и включения множеств.

(x х A  х B)  x ((х A  х B)  (х B  х A)) (*)

Зафиксируем предметную переменную х и обозначим а_х высказывание хA, b_х – высказывание х B. Получим

(а_х  b_х )  (а_х  b_х) ( b_х  а_х).

Это высказывание представляет собой логический закон 21 из п. 1.4, то есть оно справедливо независимо от его содержания, то есть от того, какой именно элемент х мы возьмем. Следовательно, будет справедливо и высказывание (*), а значит и исходное утверждение.

Далее (в п. 2.4) на основе определения равенства множеств будут сделаны определенные доказательства.