5.5. Скалярное произведение

Выше мы выяснили, что в линейном пространстве можно складывать векторы и умножать их на числа, ввели понятия базиса и линейного преобразования. Если мы хотим иметь возможность измерять длину векторов и углы между ними, то удобнее всего это сделать, используя понятие скалярного произведения. В пространстве двухмерных или трехмерных геометрических векторов скалярным произведением двух векторов называется произведение их длин, умноженное на косинус угла между ними. Это произведение обладает рядом свойств, через обязательность наличия которых определяется скалярное произведение векторов произвольного линейного пространства.

В линейном пространстве R задано скалярное произведение, если каждой паре векторов x и y из R поставлено в соответствие вещественное число (x, y) так, что для любых векторов x, y, z и любого числа α выполняются условия:

1) коммутативность (x, y)=(y, x)

2) ассоциативность относительно умножения на число (α x, y)= α (x, y)

3) дистрибутивность относительно сложения векторов (x+y, z)=(x, z)+(y, z).

Из этих условий можно легко получить следующие соотношения:

(x, α y)= α (x, y)

( z, x+y)=(z, x)+(z, y).

Линейное пространство R с заданным в нем скалярным произведением называется евклидовым, если скалярное произведение любого вектора x из R на себя самого неотрицательно , а из равенства этого скалярного произведения нулю вытекает, что и сам вектор x равен нулю

Длиной вектора x в евклидовом пространстве называется корень квадратный из его скалярного квадрата

В евклидовом пространстве для любых векторов x и y выполняется неравенство Коши-Буняковского

.

Выполнение этого неравенства делает корректным следующее определение.

Угол φ между ненулевыми векторами x и y в евклидовом пространстве определяется равенством

Пусть – базис евклидова пространства R. И известны разложения векторов x и y в этом базисе.

Тогда

При любом k

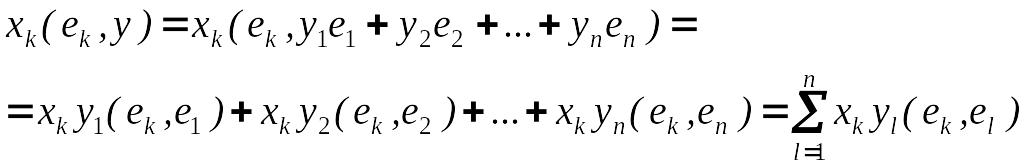
То есть

Из этой формулы очевидно, что скалярное произведение двух векторов определяется через их координаты и попарные скалярные произведения базисных векторов. Наиболее просто оно вычисляется в случае, если базис является ортонормированным.

Базис евклидового пространства называется ортонормированным, если выполняются условия

1) ортогональность: для любой пары различающихся базисных векторов

2) нормировка: для любого базисного вектора

Таким образом, если базис является ортонормированным, то в формулу суммы, по которой вычисляется скалярное произведение, входят лишь слагаемые со скалярным квадратом базисных векторов.

Пример 5.6.

Найти косинус угла между векторами векторов x и y трехмерного евклидового пространства, записанными в ортонормиро­ванном базисе,

,



7. ЛИнейное программирование

В жизни каждому человеку постоянно приходится принимать решения. И, конечно, хочется, чтобы они были оптимальными, т.е. наилучшими. Когда и сами решения, и факторы, которые надо учесть при их принятии, могут быть выражены в количественной форме, на помощь приходит математика со своей теорией принятия оптимальных решений.

Эта теория формализует совокупность действий, связанных с достижением определенных целей (ее принято называть «операцией»), например, разработку схемы перевозок, обеспечивающих снабжение населенных пунктов; выбор пищевого рациона, содержащего достаточное количество питательных веществ; планирование производства различных видов изделий. Операция характеризуется количественными факторами двух видов: неконтролируемыми (значения известны, но не зависят от воли принимающего решение) и контролируемыми (управляемыми) x₁, x₂, …, x_n (значения зависят от лица, принимающего решение, но в определенных пределах, выражаемых математическими ограничениями).

Решение – любой допустимый (удовлетворяющий ограничениям) набор значений факторов x₁, x₂, …, x_n.

Как выбрать лучшее из решений? Надо определить критерий качества решения.

Критерий качества решения, выраженный в виде функции f(x₁, …, x_n), называют критерием оптимальности, а функцию f(x₁, …, x_n ), позволяющую оценить качество решения, – целевой функцией.

Оптимальное решение – решение, на котором достигается экстремум целевой функции.

Если ограничения задаются системой линейных неравенств и целевая функция является линейной, то задача называется задачей линейного программирования.

Классической иллюстрацией задач линейного программирования служит задача о диете: найти наиболее экономный рацион при соблюдении условий питательности. Формулируется она следующим образом.

Имеется n различных продуктов F₁, F₂, ..., F_n, содержащих m различных питательных элементов N₁, N₂, ..., N_m. Каждому человеку необходимо в фиксированный период не менее ₁ единиц N₁, ..., _m единиц N_m. Известно содержание каждого питательного элемента в единице каждого из продуктов (матрица питательности):

			...
			...
...	....	....	...	.....
			...

Выбрать диету – значит определить количества ₁, ₂,…, _n единиц продуктов F₁, F₂, …, F_n .

При этом должны быть удовлетворены требования питательности:

для i=1,2,...,m. (*)

Поскольку речь идет о количествах продуктов, естественно потребовать также неотрицательность каждого из ₁, ₂,…, _n. :

для i=1, …, n. (**)

Диета, для которой выполнены условия (*) и (**), является допустимой.

Пусть для каждого продукта F_j задана его цена (за единицу) – _j.

Тогда P(₁, ₂,…, _n ) – стоимость диеты ₁, ₂,…, _n находится как:

P(₁, ₂,…, _n)=

Задача: среди всех диет, удовлетворяющих (*) и (**), найти оптимальную (ту, при которой P(₁, ₂,…, _n ) достигает минимума).

Задачи линейного программирования удобно формулировать с использованием матриц и векторов. Действительно, обозначим матрицу питательности А. Вектор-столбец  – вектор искомых количеств продуктов (n-мерный). Произведение матрицы А на вектор  задает левую часть системы ограничений.

Вектор-столбец  состоит из m компонент _i и задает правую часть системы ограничений, т.е. А   .

Стоимость диеты P(₁, ₂,…, _n ) – значение целевой функции – скалярное произведение вектора  и вектора цен .

Задача состоит в нахождении вектора , удовлетворяющего условию А    и доставляющего минимум P(₁, ₂,…, _n ) = .

Еще короче: найти: min() при А   .

Пример 6.1.

При откорме ягнят можно использовать корм с высоким содержанием белка по цене 0,80 руб./кг или более дешевый корм по цене 0,40 руб./кг. Килограмм дорогого корма дает 125 г белка и 4500 калорий, а дешевого – 50 г белка, но 7500 калорий. Одному ягненку в неделю требуется не менее 100 г белка и 4500 калорий. Найти самую дешевую смесь кормов, удовлетворяющую требованиям питательности.

Сформулируем задачу линейного программирования.

Пусть искомая смесь состоит из х₁ кг дорогого корма и х₂ кг – дешевого. Эта смесь содержит 125 х₁ +50 х₂ граммов белка и дает 4500 х₁ +7500 х₂ калорий. Таким образом, система ограничений имеет вид:

Найти такие х₁ и х ₂ , чтобы стоимость недельного рациона (0,8 х₁ + 0,4 х₂) достигала минимума. В матричном виде:

Найти min(0,8 х₁ + 0,4 х₂)

Каждое из линейных неравенств системы ограничений определяет полупространство, пересечение которых образует область допустимых решений.

Пример 6.2.

Изобразим графически область допустимых решений для примера 6.1.

Н е углубляясь в детали решения задач линейного программирования, опуская описание симплекс-метода – основного способа решения таких задач, реализованного во множестве программных продуктов. Заметим лишь, что симплекс-метод по сути определяет переход от одного допустимого решения к другому в направлении оптимизации значения целевой функции (уменьшения значения для задачи отыскания минимума и увеличения – для задачи максимизации). Если размерность задачи невелика, то решение задачи легко находится сравнением значений целевой функции в углах многогранника, задающего область допустимых решений.

Пример 6.3.

Для нахождения решения задачи из примера 6.1 требуется сравнить значения функции (0,8 х₁ + 0,4 х₂) в точках (0,2), (1,0) и (14/19, 3/19) (последняя точка – точка пересечения прямых 125х₁+50х₂=100 и 4500х₁+7500х₂=4500).

точка	Значение функции (0,8 х1 + 0,4 х2 )
(0,2)	0,8
(1,0)	0,8
(14/19, 3/19) или (0,737; 0,158)	0,65

Таким образом, решение задачи: 0,737 кг дорогого корма и 0,158 кг – дешевого.

В теории линейного программирования особая роль принадлежит двойственности. Для каждой задачи линейного программирования существует двойственная к ней. Двойственность играет особую роль и в задачах линейного программирования экономического содержания. Опишем, как строится двойственная задача, и сформулируем основную теорему линейного программирования.

Основные правила перехода к двойственной задаче:

– целевая функция изменяется на противоположную (min – на max, max – на min)

– коэффициентами аргументов целевой функции становятся бывшие правые части системы ограничений

– матрица, задающая систему ограничений, транспонируется

– правыми частями системы ограничений становятся бывшие коэффициенты аргументов целевой функции.

Формально постановку задачи, двойственной задаче о диете, можно описать так: найти такие, на которых достигается при условии для .

Содержательная постановка задачи: определить цены питательных веществ так, чтобы суммарная цена требуемого в диете количества питательных веществ была максимальной и чтобы стоимость всех питательных веществ, содержащихся в продукте, не превосходила цены единицы продукта (для всех продуктов).

Смысл двойственной задачи заключается в том, что если человек покупает продукты, чтобы удовлетворять свои потребности в питательных веществах, то найдется некто (например, продавец «Гербалайф»), кто будет продавать ему питательные вещества в чистом виде и при этом за максимально возможную цену. Но эта максимальная цена ограничена стоимостью продуктов.

Основная теорема двойственности. Если обе двойственные задачи имеют допустимые решения, то они имеют и оптимальные решения, и их значения совпадают.

Пример 6.3.

Построим задачу, двойственную задаче из примера 6.1.

Система ограничений:

Найти максимум функции (100 y₁ + 4500 y₂).

Соответствующее графическое представление: