5.4. ЛинейНые преобразования

В векторном пространстве R задано преобразование А, если каждому вектору x из R поставлен в соответствие определенный вектор А x, также принадлежащий R и называемый образом вектора x при преобразовании А. Преобразование А  называется линейным, если для любых двух векторов x и y из R и произвольного числа выполняются равенства:

1) А (x+y)= А x+ А y

2) А (αx)= α А x

Пример 5.3.

Является ли преобразование вектора х, заключающееся в изменении знака его координат, линейным?

Пусть х – вектор n- мерного пространства R.

. Тогда А x=

Очевидно, что А x=(-1)x, а признак линейности преобразования следует из свойств умножения вектора на число. Данный пример можно обобщить, сделав заключение, что умножение вектора на число является линейным преобразованием. 

Если то линейное преобразование векторов можно интерпретировать как преобразование двухмерных геометрических векторов, первая координата которых откладывается по оси абсцисс, а вторая – по оси ординат. В частности, вышерассмотренное преобразование интерпретируется как отражение вектора относительно начала координат (рис. 5.1).

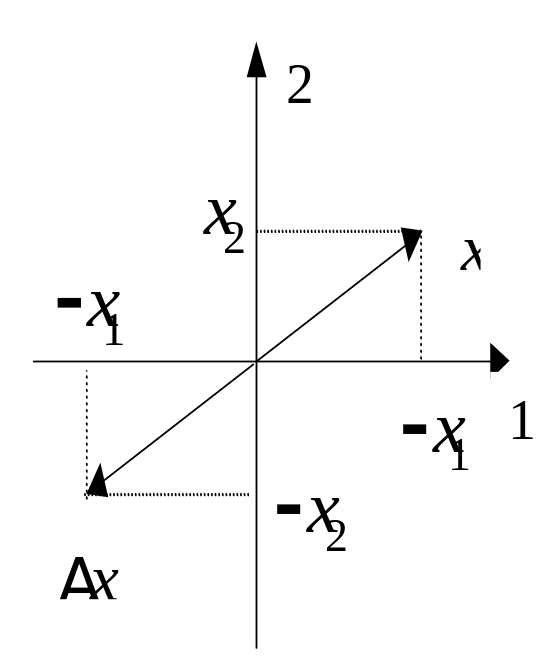
Рис. 5.1. Пример линейного преобразования – отражение двухмерного вектора относительно начала координат

Пусть – базис пространства R, то есть . Тогда в силу линейности преобразования А имеем

y=А = А + А + … + А .

Таким образом, линейное преобразование вектора x является линейной комбинацией преобразований базисных векторов, причем коэффициентами этой комбинации являются соответствующие координаты вектора x. Результат преобразования А базисного вектора (i=1, …, n) также можно разложить по базису

А = .

Подставляя это в выражение для А , получим

y= А =

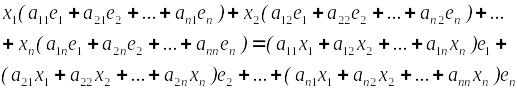
Учитывая что вектор y имеет единственное разложение по базису

,

получим выражения для координат вектора – результата преобразования А

Таким образом, каждому линейному преобразованию А в данном базисе соответствует матрица А, в которой

• столбцы образованы коэффициентами разложения векторов А по базису ;

• строки содержат коэффициенты линейной комбинации, выражающей значения i-ой координаты вектора Аx через координаты вектора x.

Пример 5.4.

Найти матрицу линейного преобразования, переводящего вектор

_{в вектор} .

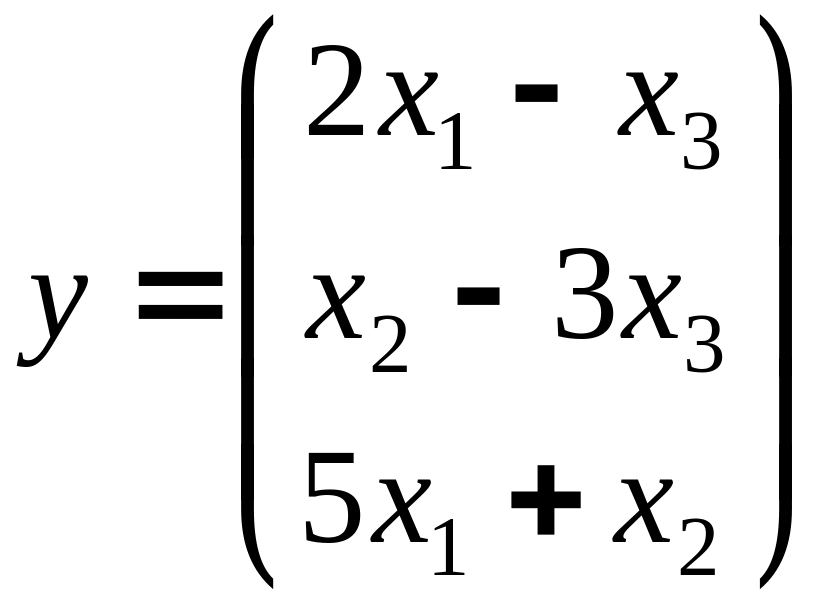Так как коэффициенты линейной комбинации, выражающей значения i-ой координаты вектора y через координаты вектора x, располагаются по строкам матрицы А, то:

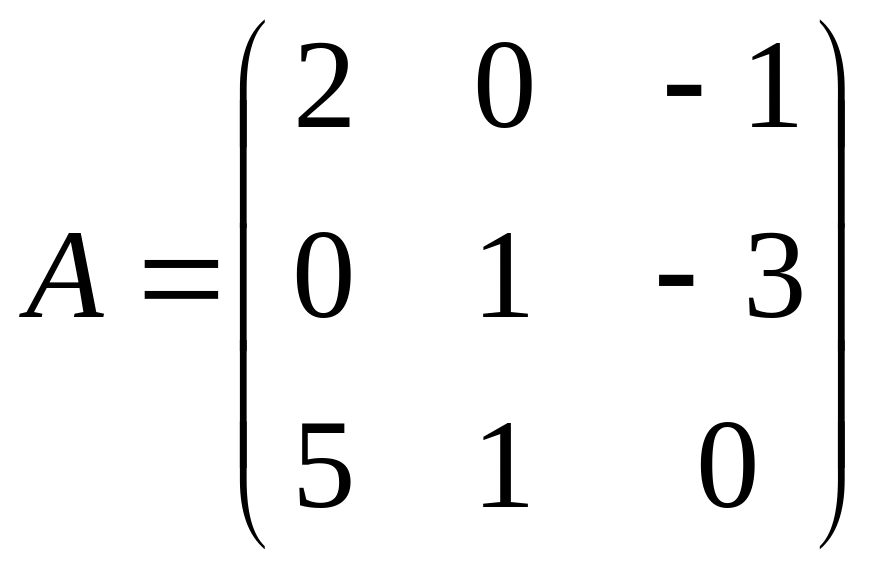
Пусть линейное преобразование А, матрица которого равна А, переводит вектор x в вектор y, то есть

y=А

Пусть другое линейное преобразование B, матрица которого равна B, переводит вектор y в вектор z, то есть

z=B y.

Тогда можно доказать, что преобразование С, заключающееся в суперпозиции, то есть в последовательном выполнении сначала линейного преобразования А, а затем линейного преобразования B будет также линейным. Поскольку

z=B y=B (А )=(B А) = C ,

то матрица C преобразования-суперпозиции С будет равна произведению матриц последовательно выполняемых преобразований, причем справа записывается матрица преобразования, которое выполняется раньше

C=B A. 

Пример 5.5.

Найти матрицы линейных преобразований векторов двухмерного пространства, заключающихся в последовательном выполнении преобразований 1) А и B, 2) B и А, где

А – изменение знака второй координаты,

B – прибавление к первой координате второй координаты, вычитание из второй координаты первой координаты.

Пусть y=А . Тогда

.

Пусть теперь y=B . Тогда

.

1)

2)

