4. Матрицы и определители

4.1. Основные понятия

Из школьного курса математики вам хорошо знакомы числовые множества, над элементами которых можно производить различные числовые операции (сложение, вычитание и другие). Используя эти множества, можно строить различные числовые функции, записывать с их помощью и решать разноообразные уравнения. Эти знания полезны при решении многих управленческих задач, например при вычислении количества денег, необходимых для реализации некоторых управленческих решений. Введя в математические построения новые математические объекты, матрицы, которые можно рассматривать как своеобразные обобщения (и усложнения) чисел, возможно не только более кратко записать уже известные вам формулы и методы расчета, но и получить удобный аппарат для решения более широкого круга управленческих задач.

Матрицей A размера mn называется таблица чисел, содержащая m строк и n столбцов.

Если необходимо явно указать размер матрицы A, то он добавляется к имени матрицы в виде нижних индексов – _mn.

Элемент матрицы A, находящийся в i-ой строке и j-ом столбце обозначается как _ij.

Матрицу записывают, помещая таблицу чисел в круглые скобки,

Допустима также следующая краткая запись матрицы с указанием ее размера mn

A_{m n}=[ij]_{m n}

Пример матрицы размера 33

Ее элемент 23

4.2. Виды матриц

Различные виды матриц определяются путем задания некоторых ограничений на их размер или/и значение их элементов.

Матрица, в которой имеется только одна строка, называется вектором-строкой

;

матрица, в которой есть только один столбец, называется вектором-столбцом

Матрица, в которой число строк равно числу столбцов, называется квадратной матрицей n-го порядка

Главной диагональю матрицы называется множество ее элементов, у которых номер строки равен номеру столбца.

Диагональной матрицей, называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали, равны нулю.

Единичной матрицей, называется диагональная матрица, у которой все элементы, принадлежащие главной диагонали, равны единице.

Верхней (нижней) треугольной матрицей называется квадратная матрица произвольного порядка, все элементы которой, стоящие под (над) главной диагональю, равны нулю.

Примером верхней треугольной матрицы является нижеприведенная матрица A, а нижней треугольной – матрица B.

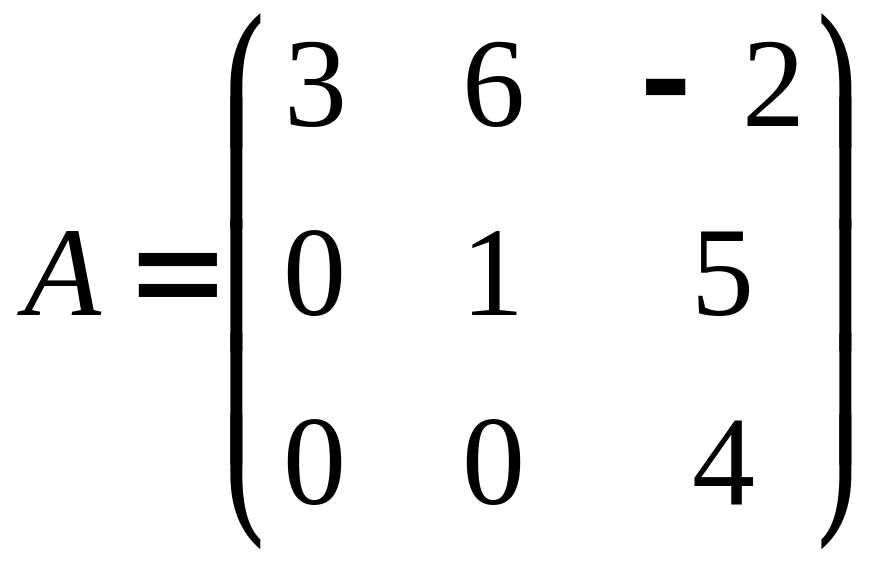
Нулевой матрицей называется матрица произвольного порядка, все элементы которой равны нулю.

0_mn=[ 0]_mn

4.3. Операции над матрицами

На множестве матриц можно определить некоторые операции, результатом выполнения которых также являются матрицы.

1. Транспонирование матрицы

Операция транспонирования является одноместной и может быть применена к любой матрице.

Результатом транспонирования матрицы размера mn является матрица размера nm, столбцы которой являются строками исходной матрицы и записаны в том же порядке.

B =A^T [b_ij]_{n m} =[_ji]_{m n}

Пример 4.1.

Пусть . Транспонированной для нее будет матрица:



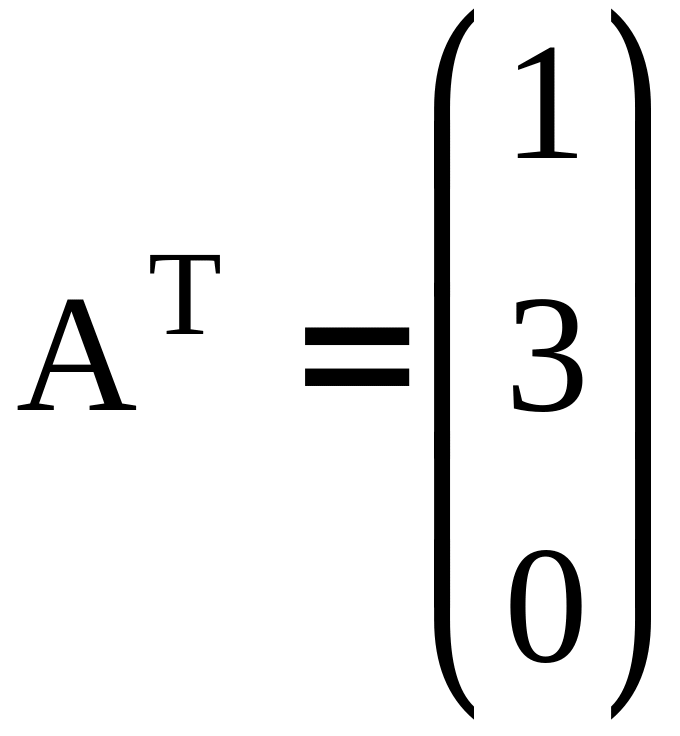
2. Умножение матрицы на число

Эта операция также является одноместной и может быть применена к любой матрице.

Результатом умножения матрицы размера mn на число  является матрица того же размера, все элементы которой равны соответствующим элементам исходной матрицы, умноженным на это число.

B_mn=A_mn [b_ij]_mn =[_ij]_mn

Пример 4.2.

Пусть .

Тогда 