3.3. Обход графа

Если G=<{v₁, v₂, …, v_n}, E> ‑ граф с n вершинами и : N_n  N_n – перестановка^*), то упорядоченное множество t = v_(1), v_(2), …, v_(n) определяет обход G.

Поскольку существует n! = 12…n различных перестановок N_n, то должно быть n! различных способов обхода графа с n вершинами. Обход начинается с вершины v_(1). Далее для определенности мы будем рассматривать упорядоченные графы и из всего множества возможных обходов рассмотрим лишь два наиболее распространенных – по глубине и по ширине.

Обход графа по глубине

Пусть G = <{v₁, …, v_n}, {L_v1, …, L_vn}> – упорядоченный граф. Выбрав начальную вершину v_s (1  s  n), имеем (1) = s. Далее вершины из t определим следующим образом:

v_(2) – первая вершина из списка смежности (то есть смежная с v_(1)),

v_(3) – первая вершина из , которой еще нет в t и т.д.,

...

v_(k) – первая вершина из , которой еще нет в t (k  4).

При этом если встречается вершина u такая, что все вершины из L_u уже содержатся в t, то процесс повторяется из вершины w  t, где w – последняя вершина в t такая, что L_w содержит вершины, не входящие в t. Обход заканчивается, когда никакая вершина из V, не входящая в t не может быть достигнута из вершин включенных в t.

Если граф G связный, то описанный выше процесс определяет обход графа G, в противном случае – обход только одной компоненты G (содержащей v_(1)). Значит, если граф G не связный, то для полного обхода надо начинать процесс в каждой связной компоненте G. Если G имеет связные компоненты V_i (1  i  p), где |V_i| = n_i, то определены n₁  n₂ …  n_p обходов по глубине; если G связный, то n обходов (так как каждая из n вершин может быть выбрана в качестве начальной).

Пример 3.8.

Для упорядоченного графа

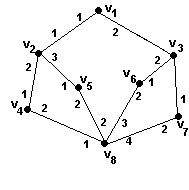
первый обход по глубине определяется так (начальная вершина v₁):

v₁, v₂, v₄, v₈, v₅, v₆, v₃, v₇  

Обход графа по ширине

Пусть G = <{v₁, …, v_n}, {L_v1, …, L_vn}> – упорядоченный граф. Выберем начальную вершину v_s и предположим, что

L_vs = <<v_s, w₁>, <v_s, w₂>, …, <v_s, w_k>>.

Тогда первые k+1 членов упорядоченного множества t определим следующим образом:

v_(1) = v_s, v_(2) = w₁, …, v_(k+1) = w_k,

а v_(k+1+i) является i-ой вершиной из L_w1, не входящей в t (i= 1,2,…). Это исчерпывает L_w1, и процесс начинается над L_w2 и т.д. Обход продолжается до того момента, пока все вершины, достижимые из v_(1), не окажутся в t. Замечание о единственности, связности и числе возможных обходов для обхода по глубине, справедливы и для обхода по ширине.

Пример 3.2.

Для графа, описанного в примере 3.1, обход по ширине с начальной вершиной v₁ задается следующим образом:

v₁, v₂, v₃, v₄, v₅, v₆, v₇, v₈  

3.4. Таблица основных понятий теории графов

№ п/п	Граф	Орграф
1	Вершина	Вершина
2	Ребро	Дуга
3	Компонента графа	Сильно связная компонента орграфа
4		Слабо связная компонента орграфа
5	Упорядоченный граф	Упорядоченный орграф
6	Дерево	Ориентированное дерево
7		Упорядоченное ориентированное дерево
8		Лист
9		Непосредственный предок
10		Непосредственный потомок
11		Предок
12		Потомок
13	Корень	Корень