3. Элементы теории графов

3.1. Вводные понятия

Графом G называется пара G=V, E, где V – непустое конечное множество вершин, а E – множество неупорядоченных пар различных вершин, называемых ребрами графа.

В дальнейшем ребро, соединяющее вершины v_i  V и v_j  V, мы будем обозначать е = {v_i, v_j}.

Вершины v_i и v_j называют смежными, если есть ребро, соединяющее эти вершины.

Графы могут быть представлены матрицами с булевыми элементами (т.е. элементами 0 и 1), поэтому многие свойства графов могут быть определены из матричных представлений путем алгебраических преобразований.

Определим матрицу смежности А графа G=V, E, где |V|=n, следующим образом:

	1, если {vi, vj}E
Aij=		(i, j =1, 2, ..., n)
	0 в противном случае

Другими словами, если вершины vi и vj являются смежными, то Aij= 1.

Следствия:

1. A_ii= 0, так как множества {v_i, v_i} по определению не принадлежат E.

2. А_ij = A_ji для всех i  j. Это следует из неупорядоченности вершин, которые соединены ребром графа. Таким образом, если {v_i, v_j}  Е, то {v_j, v_i}  Е. В результате можно определять лишь те элементы матрицы А, которые находятся выше главной диагонали, а остальную часть А симметрично отражать относительно главной диагонали.

Если e  E – ребро, а v, w  V – вершины, и если e соединяет v и w (то есть при отображении пар вершин  на ребра имеем e =  (v, w)), говорят, что e инцидентно v и w.

Матрица инцидентности (инциденций) – булева матрица n  m (где n – число вершин, m – число ребер) такая, что

		1, если j-ое ребро инцидентно i-ой вершине,
aij =	
		0, если j-ое ребро не инцидентно i-ой вершине

Замечания.

1. В любом столбце матрицы инциденций ровно два единичных элемента.

2. Связь между смежностью и инцидентностью графа может быть выражена следующим утверждением:

Любой элемент a_ij матрицы смежности равен числу ребер, инцидентных одновременно i-ой и j-ой вершинам.

Изображение графа G=V, E получается путем расположения различных точек на R² для каждой vV, причем если {v, w}  Е, мы проводим линию, соединяющую вершины v и w.

Пример 3.1.

Матрица смежности 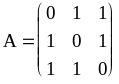дает граф из трех вершин, полностью соединенных ребрами:

v₁

v₂

v₃

Таким образом, здесь

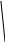
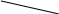
V={v₁, v₂, v₃},

E={{ v₁,v₂}, {v₂, v₃}, {v₁, v₃}},

|V|=3, |E|=3.

Пример 3.2.

Пусть V={v₁, v₂, v₃, v₄, v₅}, E={{ v₁,v₂}, {v₁, v₅}, {v₂, v₃}, {v₂, v₄}, {v₃, v₅}, {v₃, v₄}, {v₄, v₅}}, |V|=5, |E|=7.

Матрица смежности будет: а матрица инцидентности:

	0	1	0	0	1			1	1	0	0	0	0	0
	1	0	1	1	0			1	0	1	1	0	0	0
A=	0	1	0	1	1		В=	0	0	1	0	1	1	0
	0	1	1	0	1			0	0	0	1	0	1	1
	1	0	1	1	0			0	1	0	0	1	0	1

Изображений графа может быть сколько угодно много, например:



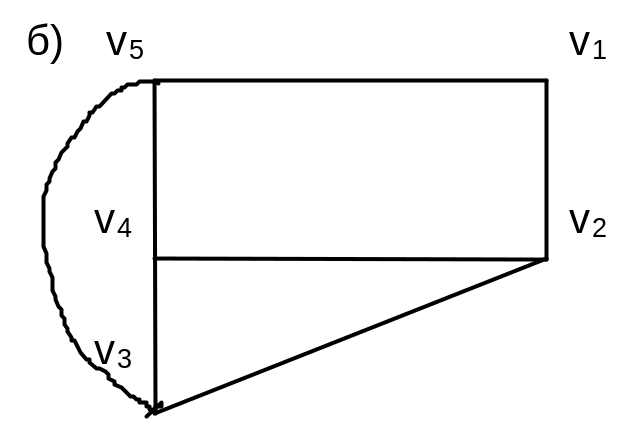
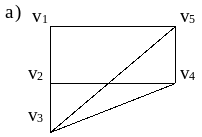
Замечание. Графы являются скорее не «геометрическими», а «топологическими» объектами, то есть они больше выражают отношения между вершинами, нежели расположение вершин и ребер в пространстве. Таким образом, граф может быть изображен бесконечным количеством разных, но «эквивалентных» способов. Во избежание неточностей понимания следует стараться не пересекать ребра графа иначе, как в вершинах (следовательно, способ изображения (а) в примере 3.2 менее предпочтителен, чем способ изображения (б)).

Маршрутом длины k из v в w в графе G= V, E называется последовательность ребер вида {v, w₁}, {w₁, w₂}, …, {w_k-2, w_k-1}, {w_k-1, w}, где вторая вершина каждого ребра совпадает с первой вершиной следующего.

Цепь – маршрут, не содержащий повторяющихся ребер.

Простая цепь – цепь, не содержащая повторяющихся вершин.

Если v=w, то маршрут называется замкнутым маршрутом или циклом.

Граф G=V, E называется связным, если каждая пара различных вершин может быть соединена маршрутом.

Обозначим через Lv список вершин, смежных с v (список смежности); Lv определяет «порядок» вершин, выходящих из v.

Множество V={v₁, …, v_n} вершин вместе с множеством {L_v1, …, L_vn} упорядоченных списков упорядоченных пар вершин называется упорядоченным графом.

Пример 3.3.

Граф, изображенный на следующем рисунке (в скобках указан порядок следования вершин в списках):

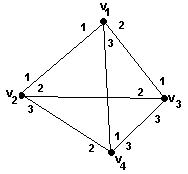
может быть записан как упорядоченный граф следующим образом:

<{v₁, v₂, v₃, v₄}, {<<v₁, v₂>, <v₁, v₃>, <v₁, v₄>>,

<<v₂, v₁>, <v₂, v₃>, <v₃, v₄>>, <<v₃, v₁>, <v₃, v₂>, <v₃, v₄>>,

<<v₄, v₁>, <v₄, v₂>, <v₄, v₃>>}> 

Любой связный ациклический граф называется деревом.

Корневое дерево – это дерево с выделенной вершиной, называемой корнем.