Теоремы о непрерывных и дифференцируемых функциях.

Определение1. Функция у=f(x) называется непрерывной в точке х₀ ,если 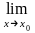f(x)=f(x₀).

Из определения 1 мы получаем

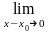f(x)= f(x₀) т.е. f(x)- f(x₀)=0, т.е. (f(x)-f(x₀))=0, т.е. f(x)=0,

здесь х=х-х₀- является приращением аргумента, а f(x)-f(x₀)=y является приращением функции. Отсюда получаем

Определение1`.Функция y=f(x) называется непрерывной в точке х_0, если y=0

Т.е. при бесконечно малом приращении аргумента приращение функции бесконечно мало.

Теорема1. Если функция y=f(x) имеет в точке х₀ производную, то она в этой точке непрерывна.

Доказательство.

Пусть f `(x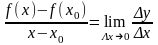<sub>0</sub>)= . Отсюда f `(x₀)=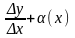 где (х)0 при х0 т.е. у=f ‘(x₀)x+(x)x. f `(x<sub>0</sub>)-const, x- бесконечно малая, т.е.f `(x₀)x- б.м.

(х) и х - оба б.м., значит (х)х- б.м., таким образом при х0 у0, следовательно у=f(x) непрерывна в точке х₀.

Теорема2. (о прохождении через нуль).

Пусть функция у=f(x) определена и непрерывна на отрезке аb (т.е. непрерывна  xa,b), пусть на концах этого отрезка она принимает значения разных знаков т.е.f(a)f(b)0. Тогда  с(a,b),что f(c)=0. (без доказательства)

Теорема3. (о прохождении через любое промежуточное значение)

Пусть f(x) определена и непрерывна на a,b, f(a)f(b), f(a)=A, f(b)=B.(либо АВ, либо ВА) Пусть ВА, тогда C(A,B)  c(a,b), что f(c)= C.

Доказательство.

Рассмотрим функцию Y(x)=f(x)-C

Y(a)=f(a)-C=A-C

Y(b)=f(b)-C=B-C Тогда Y(x) удовлетворяет теореме о прохождении через нуль, т.е.  с (a,b), Y(c)=0

Таким образом Y(c)=f(c)-C=0, следовательно f(c)=C.

Теорема4.(1-ая теорема Вейерштраса).

Если f(x) определена и непрерывна на a,b,то f(x) ограничена на a,b.(без доказательства)

Теорема5.(2-ая теорема Вейерштраса)

Если f(x) определена и непрерывна на a,b, то она достигает на a,b своего наибольшего и наименьшего значения. (без доказательства)

Геометрический смысл производной.

Рассмотрим функцию у=f(x) определённую на отрезке a,b.

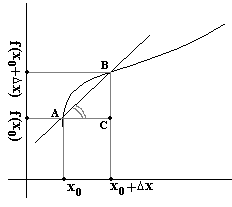
Пусть А(х₀,f(x)) и B(x+x₀, f(x₀+x))- две точки на кривой у= f(x).

Через точки А и В проходит прямая, которая является секущей для линии у=f(x).

C(x₀+x,f(x₀)), -угол между секущей и положительным направлением оси ОХ. tg= .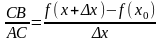

Пусть точка В движется по линии к точке А т.е. х0. Тогда в пределе точка В совпадает с точкой А секущая займёт предельное положение и превратится в касательную угол  превратится в угол  между касательной и положительным направлением оси ОХ tg превратится в tg.

tg= tg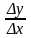= =f`(x₀).

Таким образом f`(x₀)- угловой коэффициент касательной,проведённой к линии y=f(x) в точке A(x₀, f(x₀)).(Вспомнить геометрический смысл углового коэффициента k=tg).

Тогда уравнение касательной имеет вид y-f(x₀)=f`(x<sub>0</sub>)(x-x<sub>0</sub>) или y=f(x<sub>0</sub>)+f`(x₀)(x-x₀).

Теоремы о дифференцируемых функциях.

Теорема1.(теорема Ферма).

Пусть f(x) определена и непрерывна в некоторой окрестности точки х₀, достигает максимума или минимума в точке х₀ (a,b) и имеет конечную f`(x<sub>0</sub>), то f`(x₀)=0.

Доказательство.

Допустим в точке х₀- максимум(т.е. наибольшее значение из всех возможных значений для х из данной окрестности), тогда х из этой окрестности f(x)f(x₀).

Рассмотрим 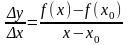, пусть хх₀, тогда f(x)f(x₀), т.е. f(x)-f(x₀)0, x-x₀0, т.е.

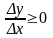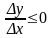0 (1), при хх₀ аналогично получаем 0 (2). Тогда перейдём к пределу в неравенствах (1) и (2) при х0. Из (1) следует, f`(x<sub>0</sub>)= , из (2) f`(x₀)= .Отсюда f`(x₀)=0. Аналогичные рассуждения для случая минимального значения f(x₀).