
- •Розділ I Математичний аналіз
- •Блок № 2
- •Блок № 3
- •Блок № 4
- •Блок № 5
- •Розділ II Аналітична і диференціальна геометрія Блок № 1
- •Лінійна алгебра Блок № 1
- •Блок № 3
- •Алгебра і теорія чисел Блок № 1
- •Блок №2
- •Блок №3
- •Розділ III Диференціальні рівняння Блок №1
- •Блок №2
- •Блок №3
- •Блок №4
- •Теорія ймовірностей та математична статистика Блок №1 Дискретний імовірнісний простір. Класична модель.
- •Блок №2 Математичне сподівання дискретної випадкової величини
- •Блок №3 Геометрична ймовірність
- •Комплексний аналіз Блок №1
- •Блок №2
- •Блок №3
- •Блок №4
Лінійна алгебра Блок № 1
|
|
A і B квадратні невироджені матриці однакових порядків, причому detA = detB. Знайти det(AB1). |
a |
b |
c |
d |
b
|
||||||||||
а) 0; |
b) 1; |
c) 1; |
d) 2. |
|||||||||||||
2. |
H підпростір дійсного векторного простору L. Яке з поданих висловлювань є вірним? |
a |
b |
c |
d |
b
|
||||||||||
а) якщо x, y є L, то (x – y) є H; |
b) якщо x є H, то 10x є H; |
|||||||||||||||
c) якщо x є H, y є L , то (x + y) є H; |
d) якщо x є L, то (–x) є H. |
|||||||||||||||
3. |
Яка з поданих систем векторів є базисом векторного простору R3? |
a |
b |
c |
d |
a
|
||||||||||
а) (1, 2, 1), (2, 3, 1), (3, 5, 1) ; |
||||||||||||||||
b) (1, 4, 1), (2, 0, 2), (1, 5, 10), (3, 2, 1) ; |
||||||||||||||||
c) (1, 0, 1), (1, 1, 1), (2, 1, 2) ; |
||||||||||||||||
d) (4, 2, 3), (0, 3, 7) . |
||||||||||||||||
4. |
Задана однорідна система із m лінійних рівнянь з n невідомими, A матриця цієї системи і rangA = k. Вказати кількість елементів у фундаментальній системі розв’язків цієї системи. |
a |
b |
c |
d |
a
|
||||||||||
а) n k; |
b) k n; |
c) m k; |
d) n + k. |
|||||||||||||
5. |
Задана сумісна система із m
лінійних рівнянь з n
невідомими, A
матриця цієї системи,
|
a |
b |
c |
d |
b
|
||||||||||
а)
|
b)
|
c)
|
d)
|
|||||||||||||
6. |
лінійне перетворення дійсного векторного простору L, x і y власні вектори із власними значеннями (1) і 0 відповідно. Знайти (2x – y). |
a |
b |
c |
d |
d
|
||||||||||
а) (2x – y) = 2x – y; |
b) (2x – y) = y – 2x; |
|||||||||||||||
c) (2x – y) = 2x; |
d) (2x – y) = –2x. |
|||||||||||||||
7. |
A і B такі матриці, що rangA = 4, rangB = 7 і добуток AB визначений. Яке з поданих висловлювань вірне? |
a |
b |
c |
d |
b
|
||||||||||
а) rang(AB) = 4; |
b) rang(AB) ≤ 4; |
c) rang(AB) > 4; |
d) rang(AB) = 28. |
|||||||||||||
8. |
Серед поданих матриць вибрати матрицю, ранг якої дорівнює числу 4. |
a |
b |
c |
d |
d
|
||||||||||
а)
|
b)
|
|||||||||||||||
c)
|
d)
|
|||||||||||||||
9. |
A квадратна невироджена матриця n–го порядку. Знайти rangA. |
a |
b |
c |
d |
c |
||||||||||
а) 1; |
b) n 1; |
c) n; |
d) n + 1. |
|||||||||||||
10. |
A і B квадратні невироджені матриці n–го порядку. Знайти rang(AB). |
a |
b |
c |
d |
b |
||||||||||
а) n 1; |
b) n; |
c) n + 1; |
d) n2. |
|||||||||||||
11. |
A квадратна матриця n–го порядку, причому detA = 0. Яке з поданих висловлювань вірне? |
a |
b |
c |
d |
a |
||||||||||
а) rangA ≤ n 1; |
b) rangA = n; |
c) rangA = n 1; |
d) rangA = 0. |
|||||||||||||
12. |
Яка з вказаних матриць обов’язково має ранг 25: |
a |
b |
c |
d |
a |
||||||||||
а) добуток двох невироджених квадратних матриць порядку 25; |
||||||||||||||||
b) добуток двох невироджених квадратних матриць порядку 5; |
||||||||||||||||
c) вироджена квадратна матриця порядку 26; |
||||||||||||||||
d) сума двох невироджених квадратних матриць порядку 25. |
||||||||||||||||
13. |
Яка із поданих підмножин векторного простору R5 є тривимірним підпростором простору R5? |
a |
b |
c |
d |
c |
||||||||||
а) ( , , , 2 + 2 + 2, 0 ) | , , R; |
||||||||||||||||
b) ( , 0, , 0, 0 ) | , R; |
||||||||||||||||
c) ( , 2, , , ) | , , R; |
||||||||||||||||
d) ( 0, , , 4 + 3, 0 ) | , R. |
||||||||||||||||
14. |
{a, b, c} лінійно незалежна система векторів дійсного векторного простору L. Яка з поданих систем векторів також є лінійно незалежною системою векторів у просторі L? |
a |
b |
c |
d |
a |
||||||||||
а) {a, a +b, a + b +c}; |
b) {a, b, a + b}; |
|||||||||||||||
c) {2a, 3b, 4c, a + b + c}; |
d) {a, 3a, –a}. |
|||||||||||||||
15. |
Який з поданих векторних просторів ізоморфний векторному простору R4 ? |
a |
b |
c |
d |
c |
||||||||||
а) R2; |
b) R3; |
c) M2(R); |
d) M4(R). |
|||||||||||||
Блок № 2
|
||||||||||||||||
1. |
Нехай
|
a |
b |
c |
d |
b |
||||||||||
a)
|
b)
|
c)
|
d)
|
|||||||||||||
2. |
Вектор x
векторного простору L
в базисі {e1,
e2, e3}
має координати
|
a |
b |
c |
d |
d |
||||||||||
а)
|
b)
|
|||||||||||||||
c)
|
d)
|
|||||||||||||||
3. |
лінійне перетворення дійсного векторного простору L, яке в базисі
{e1,
e2, e3}
простору L має
матрицю
|
a |
b |
c |
d |
c |
||||||||||
а)
|
b)
|
|||||||||||||||
c)
|
d)
|
|||||||||||||||
4. |
Лінійне перетворення
дійсного векторного простору L
в базисі {e1,
e2, e3}
простору L має
матрицю
Знайти (x), якщо x = 2e1 – e3. |
a |
b |
c |
d |
a |
||||||||||
а) (x) = e1 – 2e3; |
b) (x) = –2e1 + e3; |
|||||||||||||||
c) (x) = –e1 – e2 – e3; |
d) (x) = –e1 – e2 + 2e3. |
|||||||||||||||
5. |
f – лінійне перетворення векторного простору R2, задане за правилом: f( (x, y) ) = ( y, x ). Який з поданих векторів є власним вектором лінійного перетворення f? |
a |
b |
c |
d |
c |
||||||||||
а) ( 0, 0 ); |
b) ( 1, 2 ); |
c) ( 2, –2 ) |
d) ( 0, 1 ). |
|||||||||||||
6. |
лінійне перетворення дійсного тривимірного векторного простору L, яке в деякому базисі простору L має матрицю
Знайти множину всіх власних значень . |
a |
b |
c |
d |
d |
||||||||||
а) 1; 2; 3; |
b) 1; 4; 9; |
c) 3; 2; 3; |
d) 3; 3; 4. |
|||||||||||||
7. |
Лінійне перетворення дійсного векторного простору L в базисі {e1, e2} простору L має матрицю
Знайти матрицю в базисі {–e2, –e1}. |
a |
b |
c |
d |
a |
||||||||||
а)
|
b)
|
c)
|
d)
|
|||||||||||||
8. |
Лінійне перетворення дійсного векторного простору Rn ( n 3 ) задане за правилом: (x1, x2, x3, , xn1, xn) = (x1 + x2, x2 + x3, , xn1 + xn, 2xn). Який із поданих векторів є власним вектором перетворення , якому відповідає власне значення 2. |
a |
b |
c |
d |
d |
||||||||||
а) (2, 0, 0, , 0); |
b) (1, 2, 3, , n); |
c) (0, 0, 0, , 0); |
d) (3, 3, 3, , 3). |
|||||||||||||
9. |
лінійне перетворення дійсного векторного простору L, яке в базисі {e1, e2} простору L має матрицю
Який із поданих векторів є власним вектором ? |
a |
b |
c |
d |
a |
||||||||||
а) 2e1; |
b) e1 + e2; |
c) e1 – e2; |
d) e2. |
|||||||||||||
10. |
A
матриця несумісної системи лінійних
рівнянь,
розширена матриця цієї системи і
rangA = n.
Знайти
|
a |
b |
c |
d |
d |
||||||||||
а) 1; |
b) n 1; |
c) n; |
d) n + 1. |
|||||||||||||
11. |
Яка із вказаних систем лінійних рівнянь завжди є сумісною? |
a |
b |
c |
d |
a |
||||||||||
а) однорідна система із n лінійних рівнянь, кількість невідомих в якій дорівнює (n 1); |
||||||||||||||||
b) неоднорідна система із n лінійних рівнянь з n невідомими; |
||||||||||||||||
c) неоднорідна система із n лінійних рівнянь, кількість невідомих в якій дорівнює (n + 1); |
||||||||||||||||
d) неоднорідна система із n лінійних рівнянь, ранг матриці якої дорівнює (n 1). |
||||||||||||||||
12. |
A і B квадратні матриці n–го порядку ( n 3), причому rangA = n, rangB = n 1. Яке з поданих висловлювань вірне? |
a |
b |
c |
d |
a |
||||||||||
а) rang(AB) = n 1; |
b) rang(AB) = n; |
|||||||||||||||
c) rang(AB) = n2 n; |
d) rang(AB) n 2. |
|||||||||||||||
13. |
H ненульовий підпростір векторного простору R2, H R2. Знайти dimRH. |
a |
b |
c |
d |
b |
||||||||||
а) 0; |
б) 1; |
c) 2; |
d) 4. |
|||||||||||||
14. |
Одним із базисів дійсного векторного простору L є система {e1, e2, e3}. Яка із поданих систем векторів також є базисом простору L? |
a |
b |
c |
d |
b |
||||||||||
а) {e1, e2}; |
b) {3e1, 2e3, –e2}; |
|||||||||||||||
c) {2e1, 5e3, e1 – 4e3}; |
d) {e1, e2, e1 +e2}. |
|||||||||||||||
15. |
Одним із базисів дійсного векторного простору L є система {e1, e2, …, en}. Яка із поданих систем векторів також є базисом простору L? |
a |
b |
c |
d |
b |
||||||||||
а) {e1, e2, …, en–1, e1 + e2 + … + en–1}; |
b) {e1, 2e2, …, nen}; |
|||||||||||||||
c) {e1, 2e1, …, ne1}; |
d) {e1 + e2, e2 + e3, …, en–1 + en }. |
|||||||||||||||

 ;
;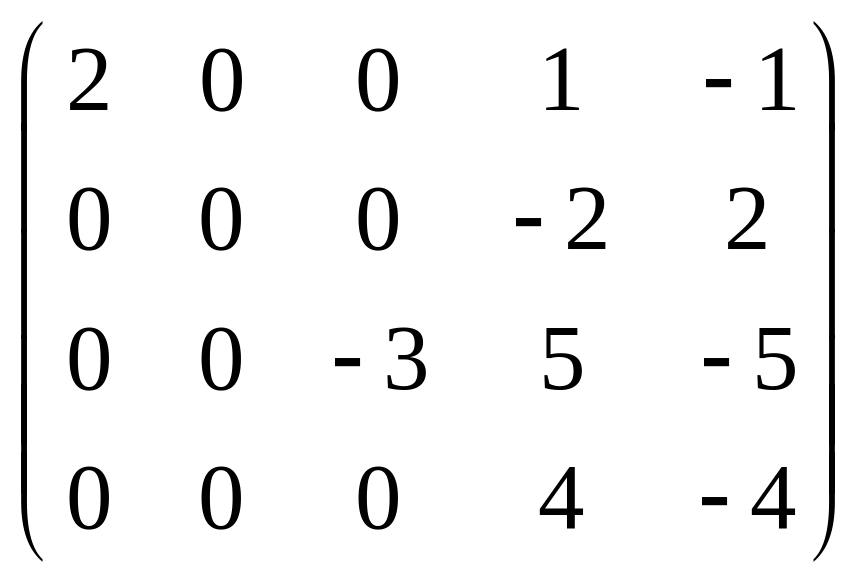 ;
;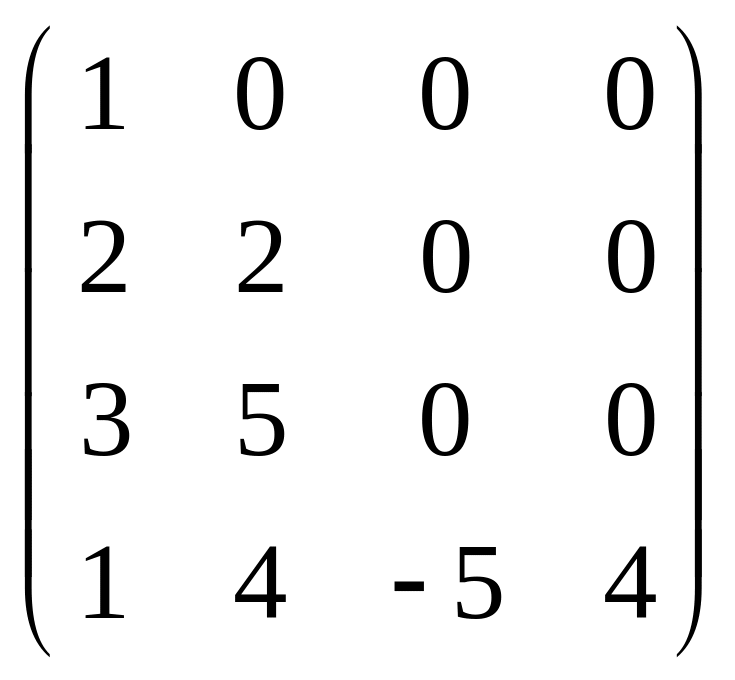 ;
;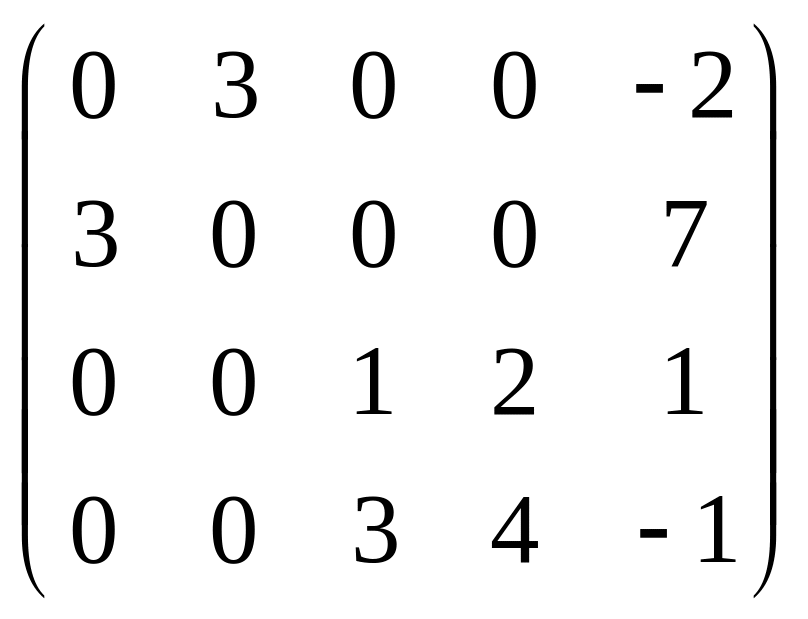 .
.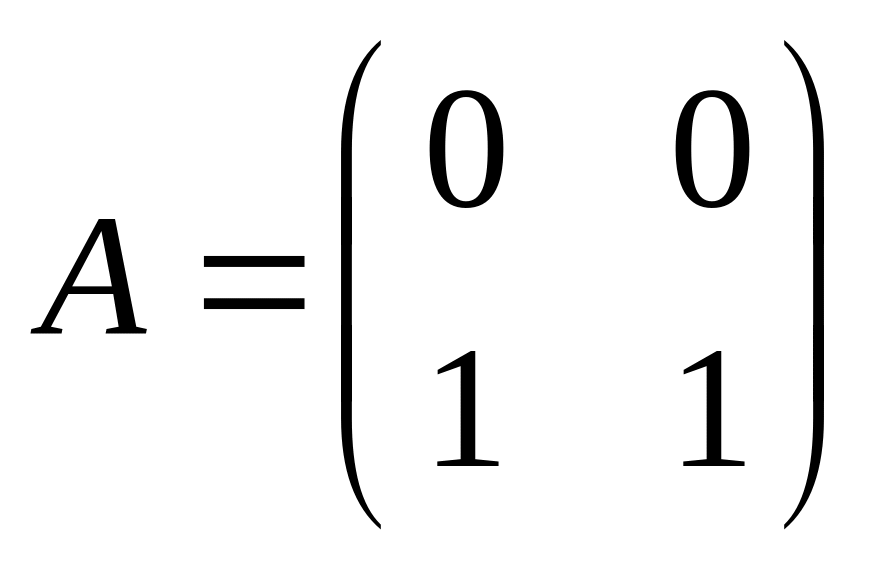 ,
,
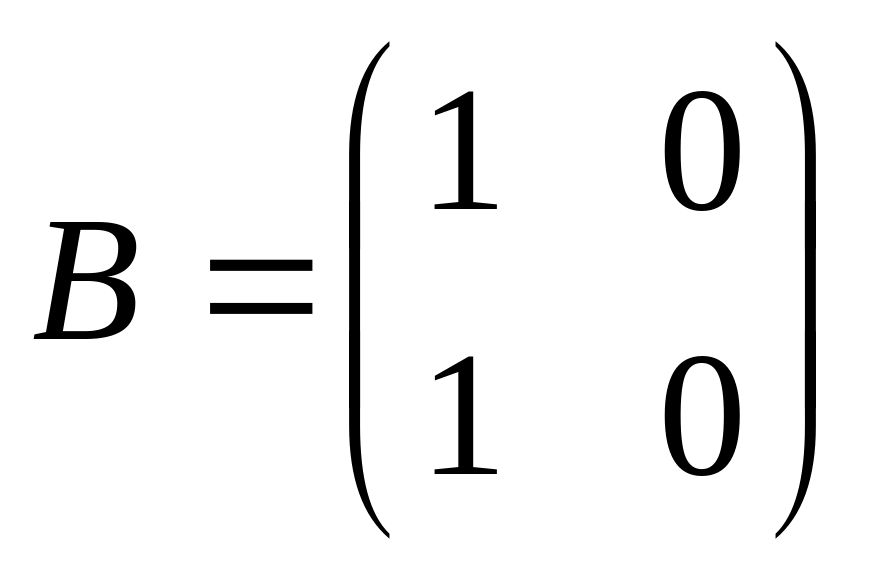 .
Знайти матрицю C,
якщо
.
Знайти матрицю C,
якщо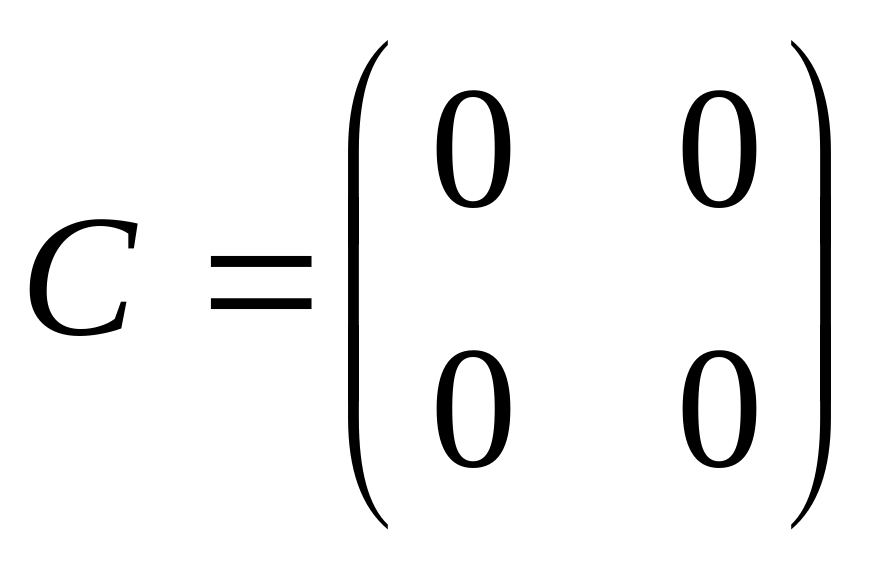 ;
;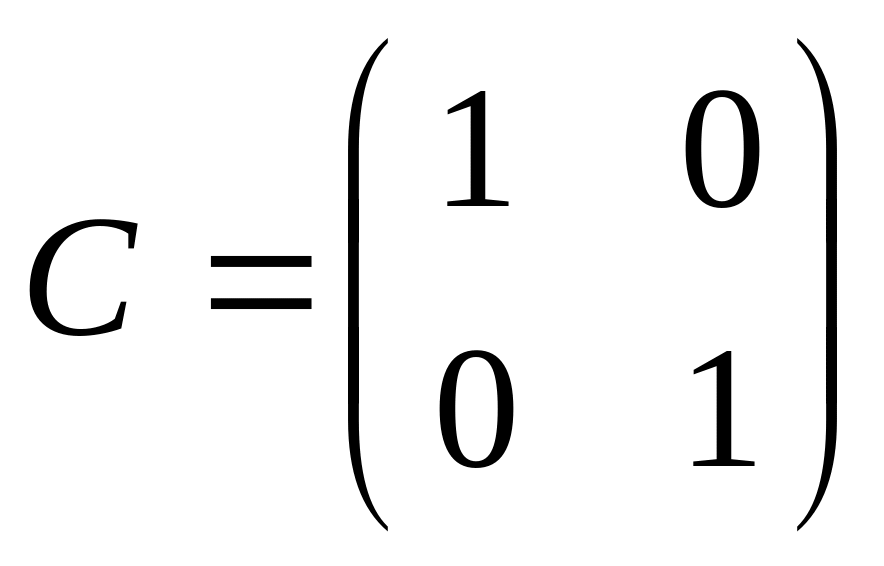 ;
;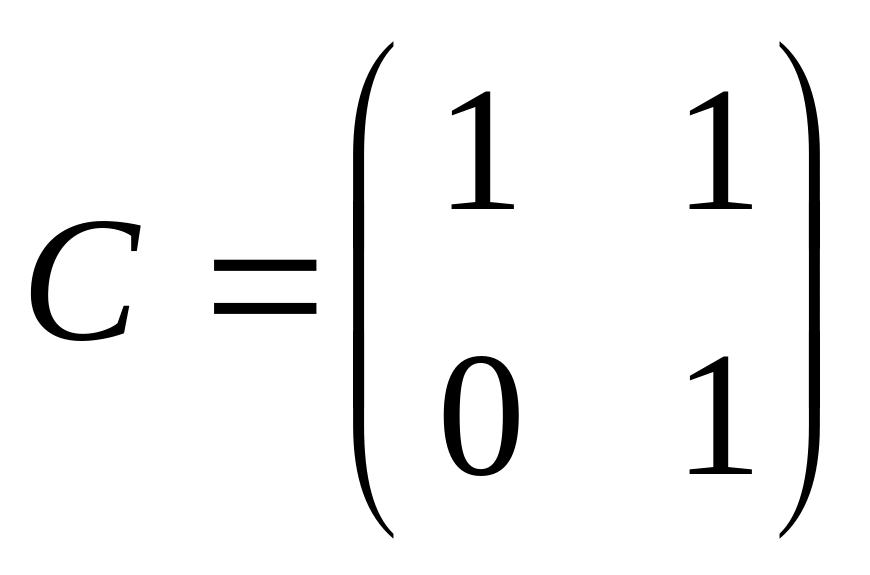 ;
; .
.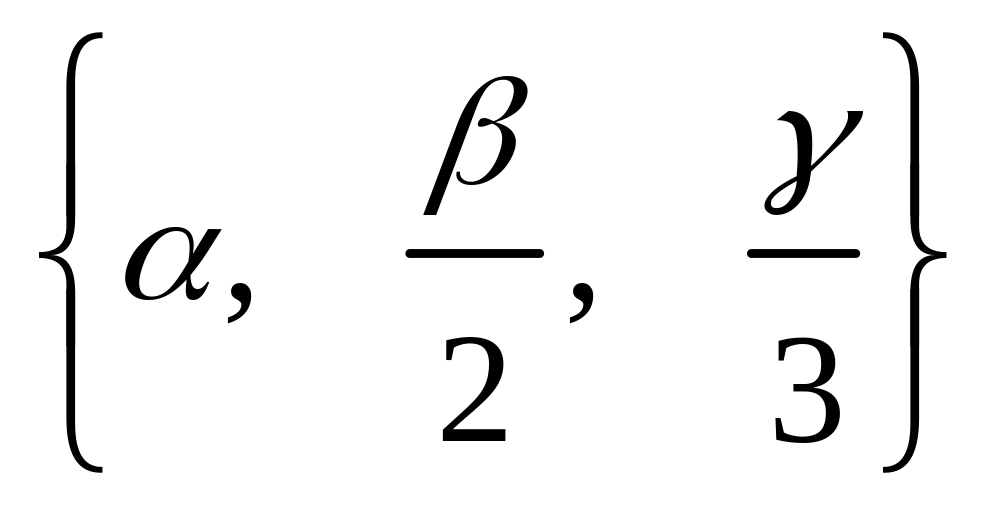 ;
;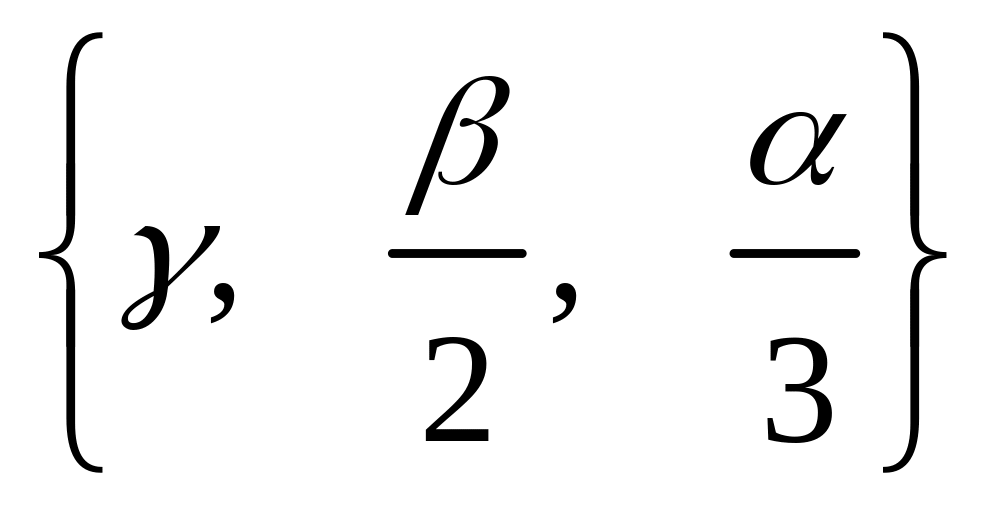 .
.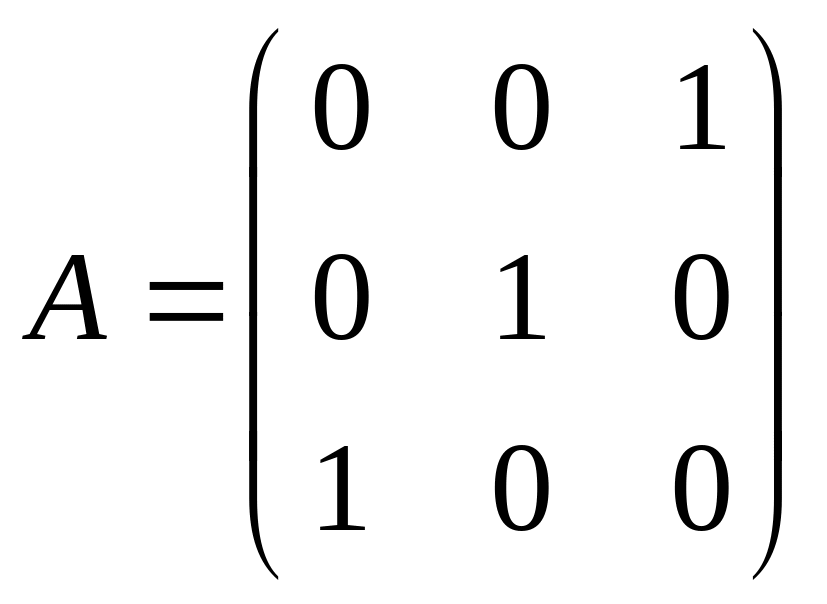 .
Знайти матрицю
.
Знайти матрицю
 ;
;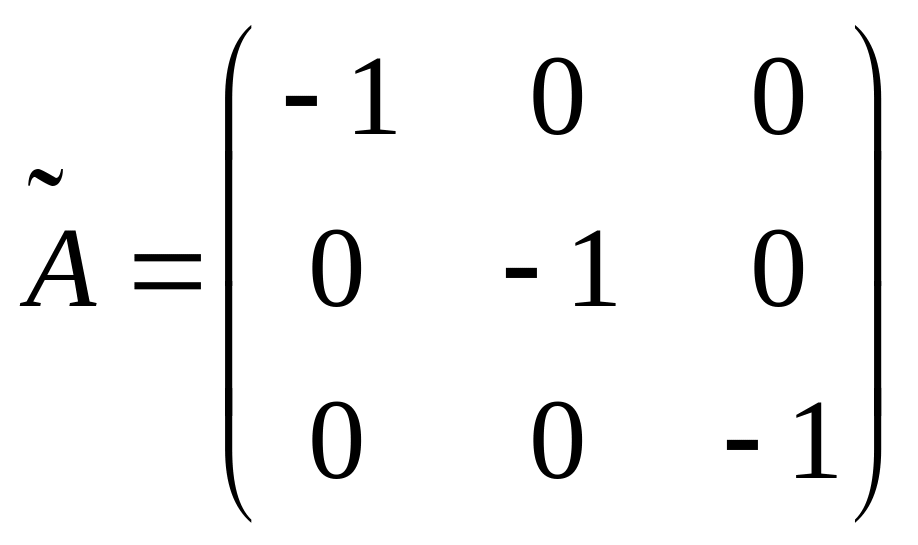 ;
;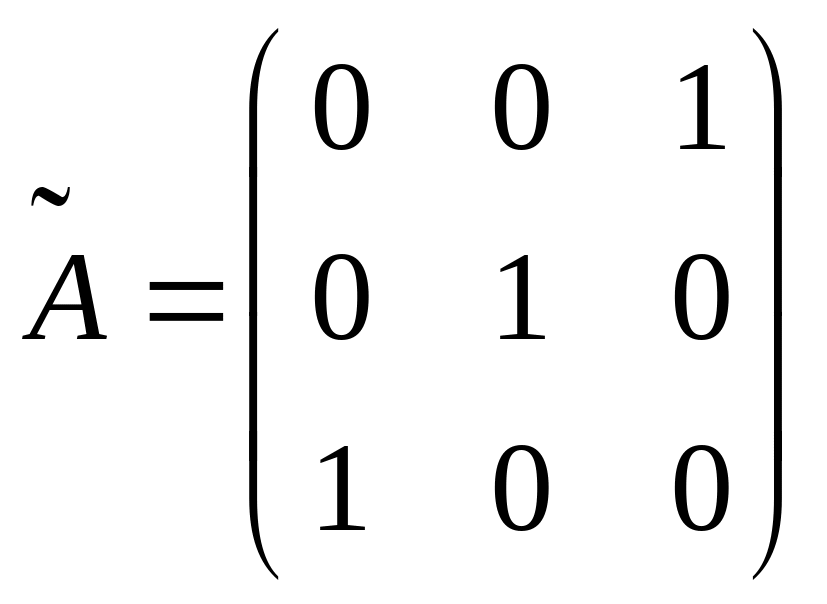 ;
;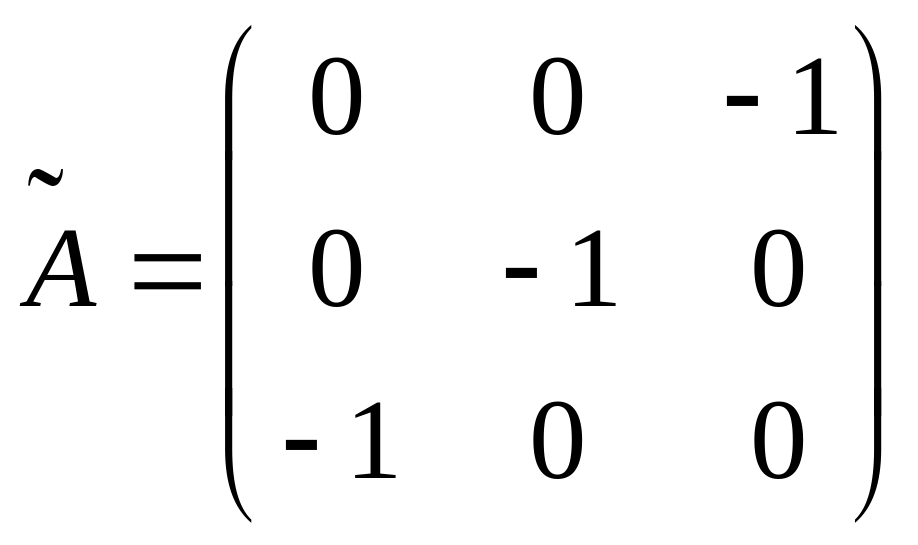 .
.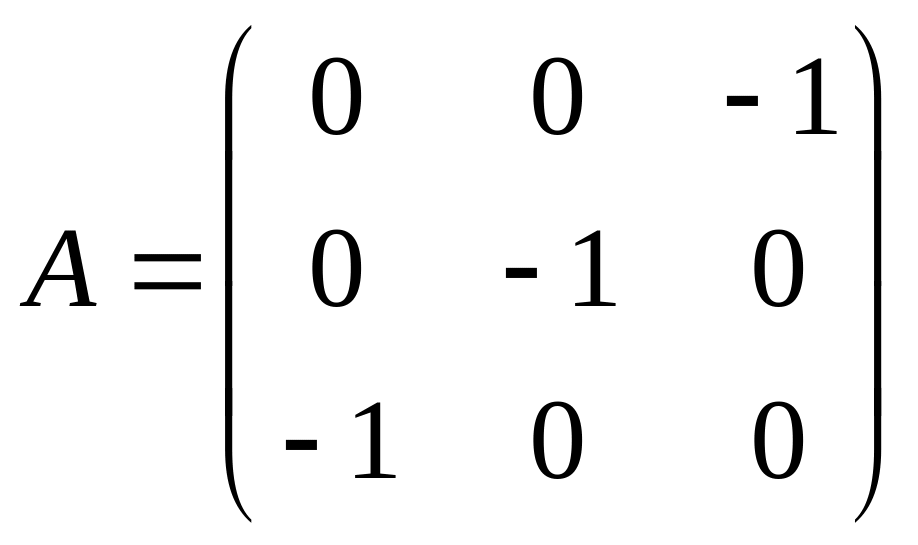 .
. .
.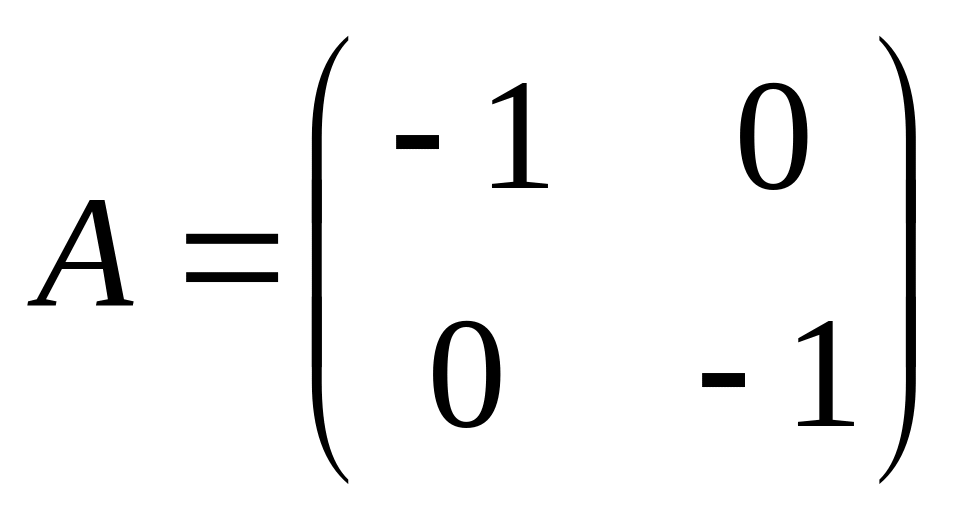 .
.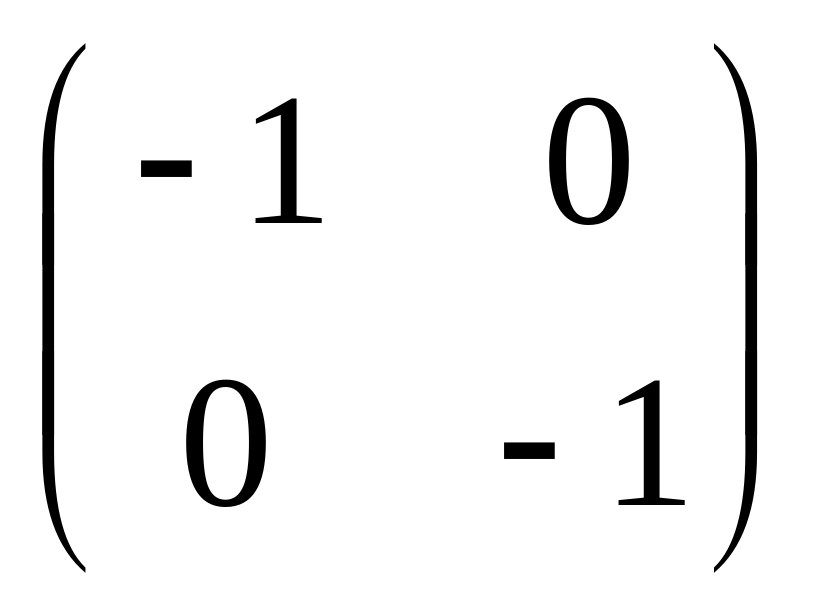 ;
;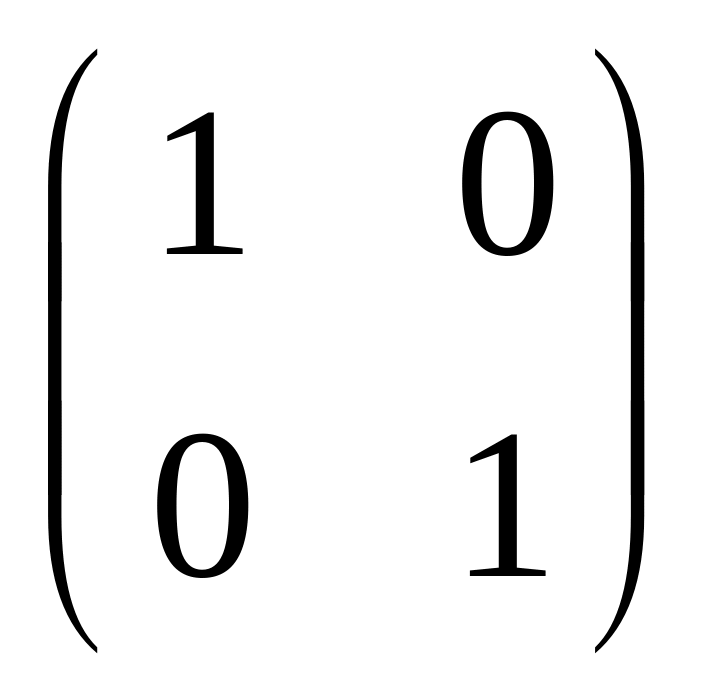 ;
;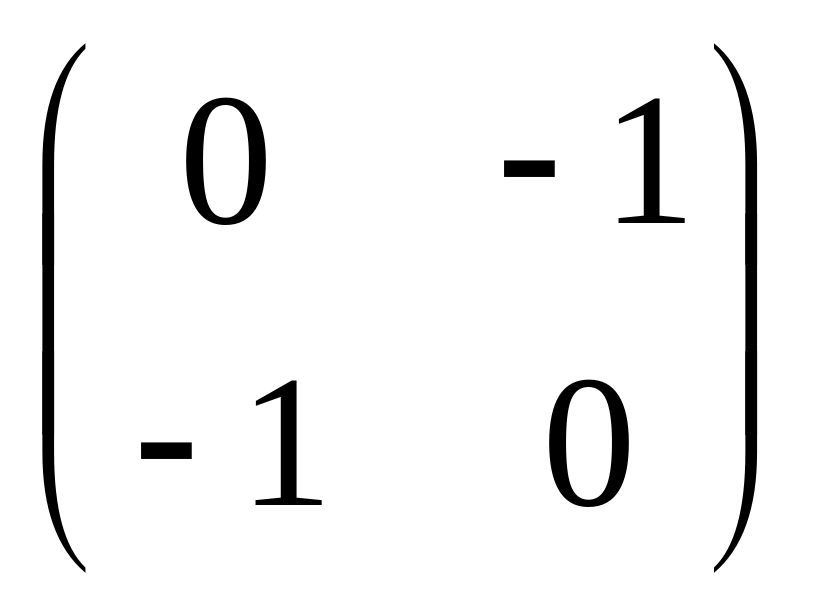 ;
;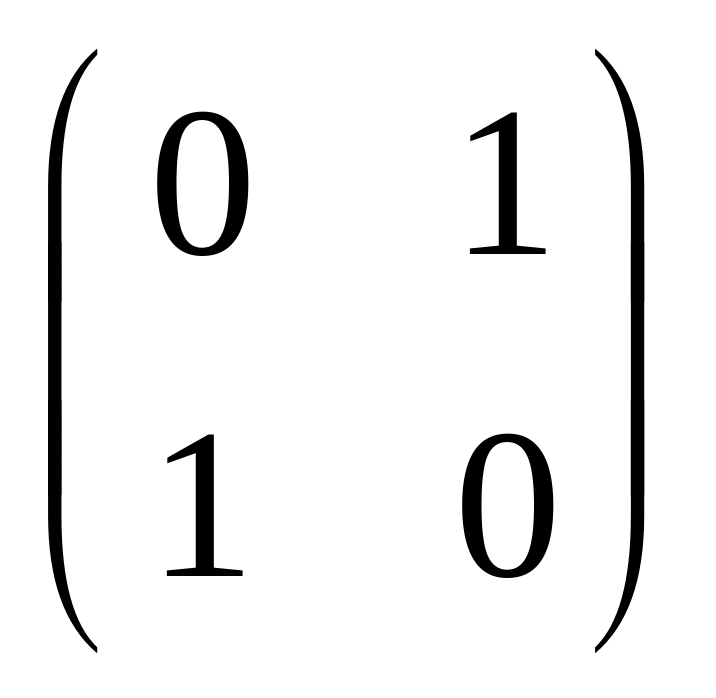 .
. .
.