Определение объема выборки.

Для повторной выборки:

, где  - допустимая погрешность (ошибка), t – нормированное отклонение от среднего значения.

Для бесповторной выборки:

Погрешность () задается исследователем, значение t определяется по таблицам F(t) в зависимости от заданной доверительной вероятности (0,95).

Чем больше вероятность, тем уже вероятность ответа.

Методы оценки дисперсии генеральной совокупности перед проведением наблюдения.

1. По данным предыдущих исследований.

2. Если известно примерное значение среднего, то .

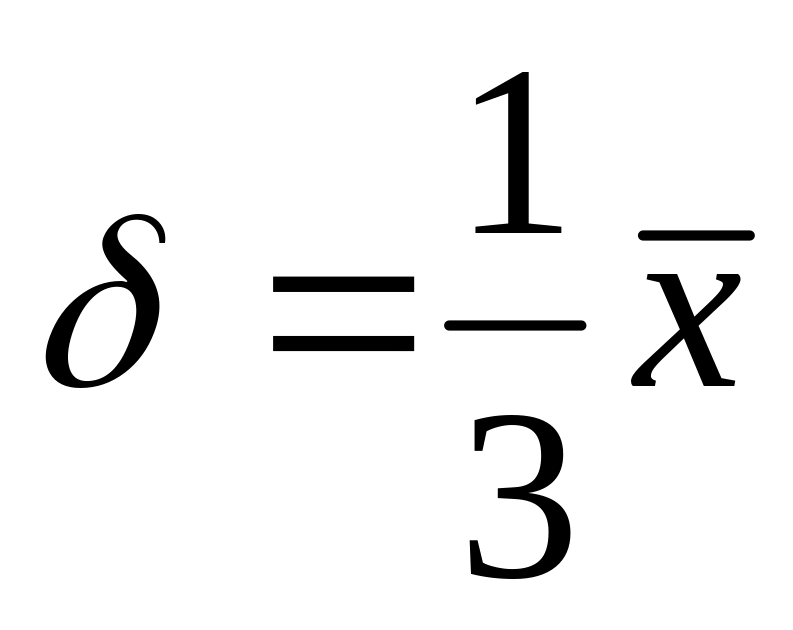3. Если известны max и min значения исследуемого показателя и распределение является нормальным, то .

4. Если известны max и min значения исследуемого показателя и распределение является ассиметричным, то .

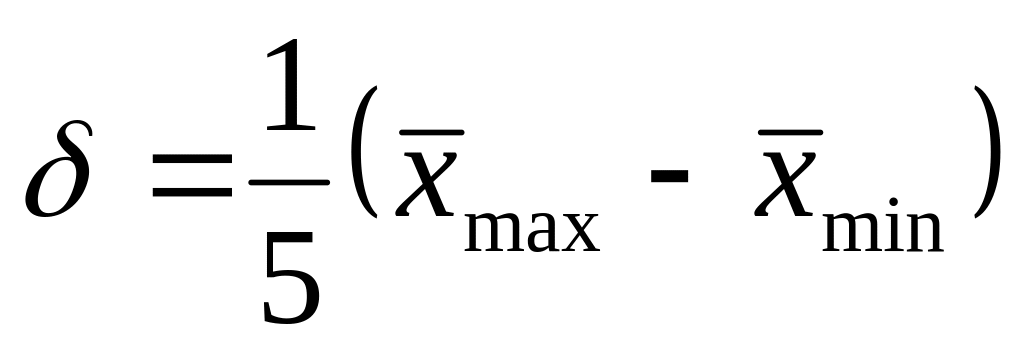5. Если исследуемый показатель является долей, то .

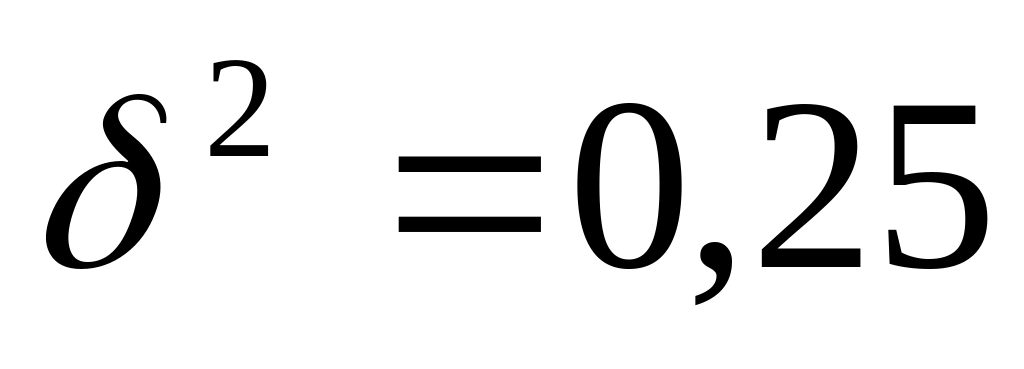При проведении исследования нескольких показателей V выборки рассчитывается по каждому из них.

При отношении  6 для всех показателей принимается n_max.

При отношении для всех показателей проводится многофазный отбор, т.е. для каждого показателя устанавливается свой V выборки.

Определение средней и предельной ошибки выборки.

Вид выборки	Выборное среднее	Выборная доля
Повторная
n  30 (малая)
n > 30
Бесповторная
n  30 (малая)
n > 30
Все виды

Пример определения средней ошибки выборки.

Из партии электрических лампочек, размером 50000 взята выборка V = 100 ламп. При проверке установлено, что 10 из них работали менее 1410 часов (продукция сроком действия менее 1410 часов считается некачественной). С вероятностью 0,954 требуется определить количество бракованных изделий в партии.

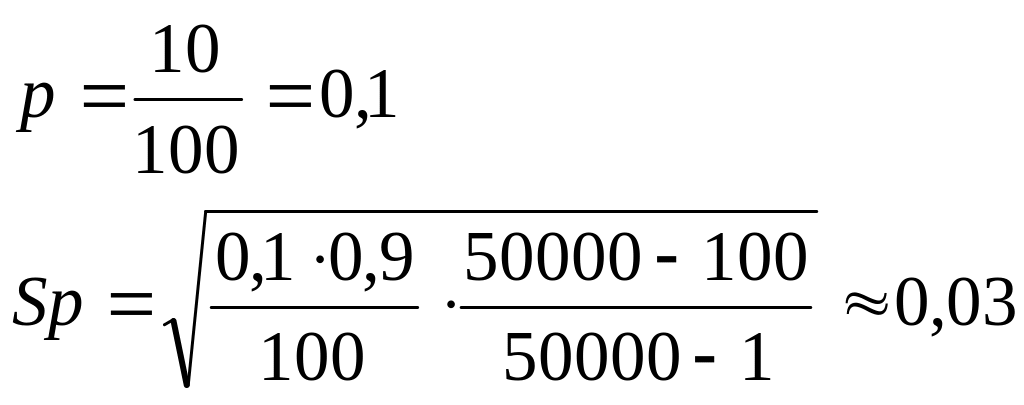
Заданна доверительная вероятность = 0,954

F(t)  = 0.954  смотрим по таблице t = 2.

Доля бракованной продукции в партии от 4% до 16%.

Определение вероятности попадания в заданные пределы

1.   x

  p

Вероятность попадания в заданные пределы равна заданной доверительной вероятности.

2.   x

  p

Решение задачи заключается в поиске значения F(t) на основе решения уравнения.

– для среднего

– для доли

Пример:

Из партии электрических лампочек, размером 50000 взята выборка V = 100 ламп. Средняя продолжительность работы ламп в выборке равна 1420 часов. Среднее квадратичное отклонение – 1 час. (Продукция сроком действия менее 1410 часов считается некачественной). Доверительная вероятность равна 0,954. Определить вероятность попадания в допустимые пределы и количество бракованных изделий в партии.

Средняя ошибка выборки:

p = 0.954  t = 2

часа

 = 10 часов – допустимая погрешность (1420-1410)

Т.к.   – составляем уравнение.

10 = t6,1

t = 1,64   = 0,9 – вероятность попадания в заданные пределы.

500000,05 = 2500 – количество бракованных ламп в партии.