Расчет средних и показателей вариации.

Виды средних:

1) Среднее арифметическое:

2) Средняя взвешенная:

, где f_i – частота повторения i-того признака.

3) Неявное среднее:

, где y – общая сумма значений показателей.

4) Среднее хронологическое:

5) Среднее квадратичное:

6) Среднее кубическое:

7) Среднее геометрическое:

8) Среднее гармоническое:

9) Взвешенное среднее гармоническое:

, где W_i – весовой коэффициент единицы совокупности.

Пример:

2 и 5

Изучение вариации. Построение вариационного ряда.

Виды вариационных рядов:

1. Ранжированный – это последовательность единиц совокупности, расположенных в порядке возрастания или убывания. (14,9 16,3 21,4 25,2 30,3)

2. Дискретный – это таблица, состоящая из 2-х колонок: 1-я – значение признака, 2-я – частота их появления.

Число проданных авто	Число дней
0	21
1	41
2	41
3	37
4	19
5	21
Итого:	180

1. Интервальный ряд – используется, когда признак принимает любые значения или признак является дискретным, но число значений велико.

Рентабельность, % xj	Число предприятий, fj	Середина интервала, xj	Накопленная частота
			fj'	fj''
10-20	1	15	1	21
20-30	5	25	6	20
30-40	12	35	18	15
40-50	2	45	20	3
50-60	1	55	21	1
Итого:	21

f_j' – количество единиц совокупности, у которых значение признака не больше, чем верхняя граница интервала.

f_j'' - количество единиц совокупности, у которых значение признака больше, чем верхняя граница интервала.

Первым этапом анализа вариационного ряда является построение гистограммы и полигона.

I-ый этап – гистограмма и полигон.

Г истограмма строится для интервального ряда.

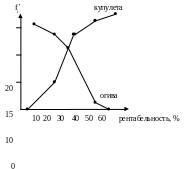
Полигон строится для интервального и дискретного ряда.

II-ой этап – расчет структурных средних

(Медианы, квартилий и мозы).

Медиана

Медиана – величина анализируемого признака, которая делит совокупность на 2 части, равные по числу единиц.

В ранжированном ряду, медиана – это средняя в ряду единиц совокупности.

14,9 16,3 21,4 25,2 30,3 (Ме = 21,4)

В дискретном ряду:

xi	fi	fi'
0	21	21
1	41	62
2	41	103
3	37	140
4	19	159
5	2 1	180
Итого:	180	180

Для определения медианы сначала определяются накопленные частоты.

Определяется номер единицы, которая делит совокупность на 2 части.

180/2 = 90

Медианой является значение признака, для которой накопленная частота больше или равна половине численности совокупности. Ме = 2

В интервальном ряду:

Определяем интервал, в котором находится эта единица, по накопленной частоте.

, где x₀ – нижняя граница медианного интервала, f '_Me–1 – частота попадания в интервал, предшествующий медианному, f_Me–1 – частота попадания в медианный интервал, i – ширина медианного интервала.

Квартили

Квартиль – это значения анализируемого признака, которые делят совокупность на 4 части, равные по … единицу.

Q ₂ – это медиана.

Для интервального ряда:

Мода

Мода – это значение признака, которое встречается чаще всего.

В ранжированном ряду моды нет.

В дискретном ряду: М₀ = {1, 2}.

В интервальном ряду:

Что бы найти моду в интервальном ряду, надо выделить интервал с максимальной частотой попадания.

, где – частота попадания в модальный интервал, – частота попадания в предшествующий интервал, – частота попадания в следующий интервал.

Если группировка выполнена с неравными интервалами, то моза определяется не по частоте, а по плотности распределения (частота, деленная на ширину интервала).

III-ий этап – расчет среднего анализирующего признака.

x – среднее взвешенное.

Правило:

Если распределение близко к нормальному, то медиана находится между мозой и среднем значением, причем ближе к среднему.

 нормальное распределение.