28. Теорема о связи сущ-ния произв. И непрерывности в точке
(т) если ф-ция дифференцируема в (.) х, то она непрерывна в ней.
Док-во: пусть ф-ция y=f(x) дифференцируема в некоторой (.) х => сущ-ет limDу/Dх(при Dх->0)=f`(x)(из определения произв.) Отсюда [ по (т) о связи ф-ции, ее предела и бмф (бил. 11): Если ф-ция имеет lim=A (при х->x0), то ее можно представить в виде суммы числа А и бмф а(х), те lim f(x)=A при х->x0 , то f(x)=A+a(x) ] имеем Dу/Dх=f`(x)+a, где а->0, при Dх->0, те Dy=f`(x)*Dx+a*Dx. Переходя к пределу, при Dх->0, получаем limDy(при Dх->0)=0. А это и означает, что ф-ция y=f(x) непрерывна в т.x (согласно 2ому опред. непрерывности ф-ции в точке)
?? Док-во 2: т к ф-ция дифф. в (.) х0, то ее приращение мб представлено в виде Dу=A*Dx+a(Dx)*Dx [ по (т) о дифференцируемости ф-ции в точке (бил.33: Для того, чтобы ф-ция y=f(x) была дифференцируемой в (.) х0 необходимо и достаточно, чтобы она имела в этой точке конечную производную] Перейдём к lim при Dx->0: limDy(при Dx->0)=lim(A*Dx+a(Dx)*Dx)(при Dх->0)=0
Следовательно, ф-ция непрерывна согласно 2ому опред. непрерывности.
29. Правила вычисления произв, связна. С арифм. Действиями
Пусть u=u(x) и v=v(x) дифференц. в (.) x0
1). Производная суммы/разночти = сумме/разности этих производных. Док-во:
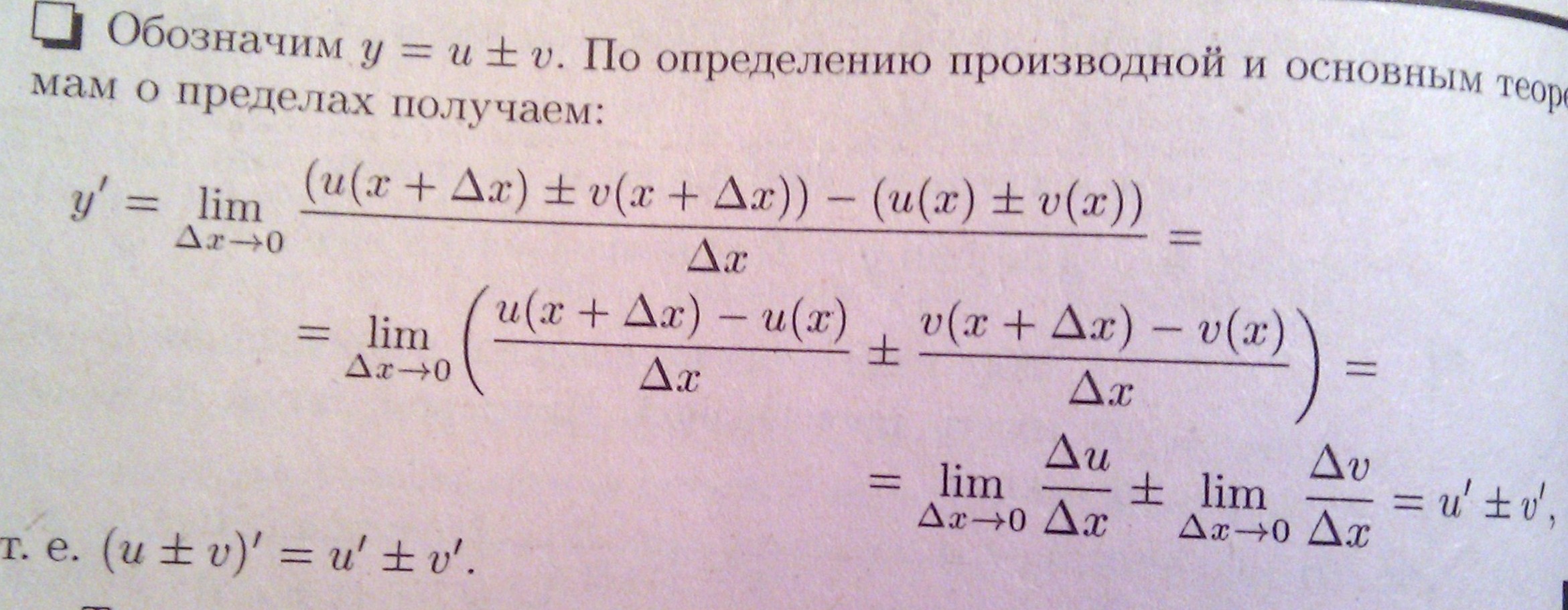
2) Производной произв. 2х = произведению производной 1 сомножителя на второй плюс произведение 1 сомножителя на произв. второго: (u*v)`=u`*v+v`*u
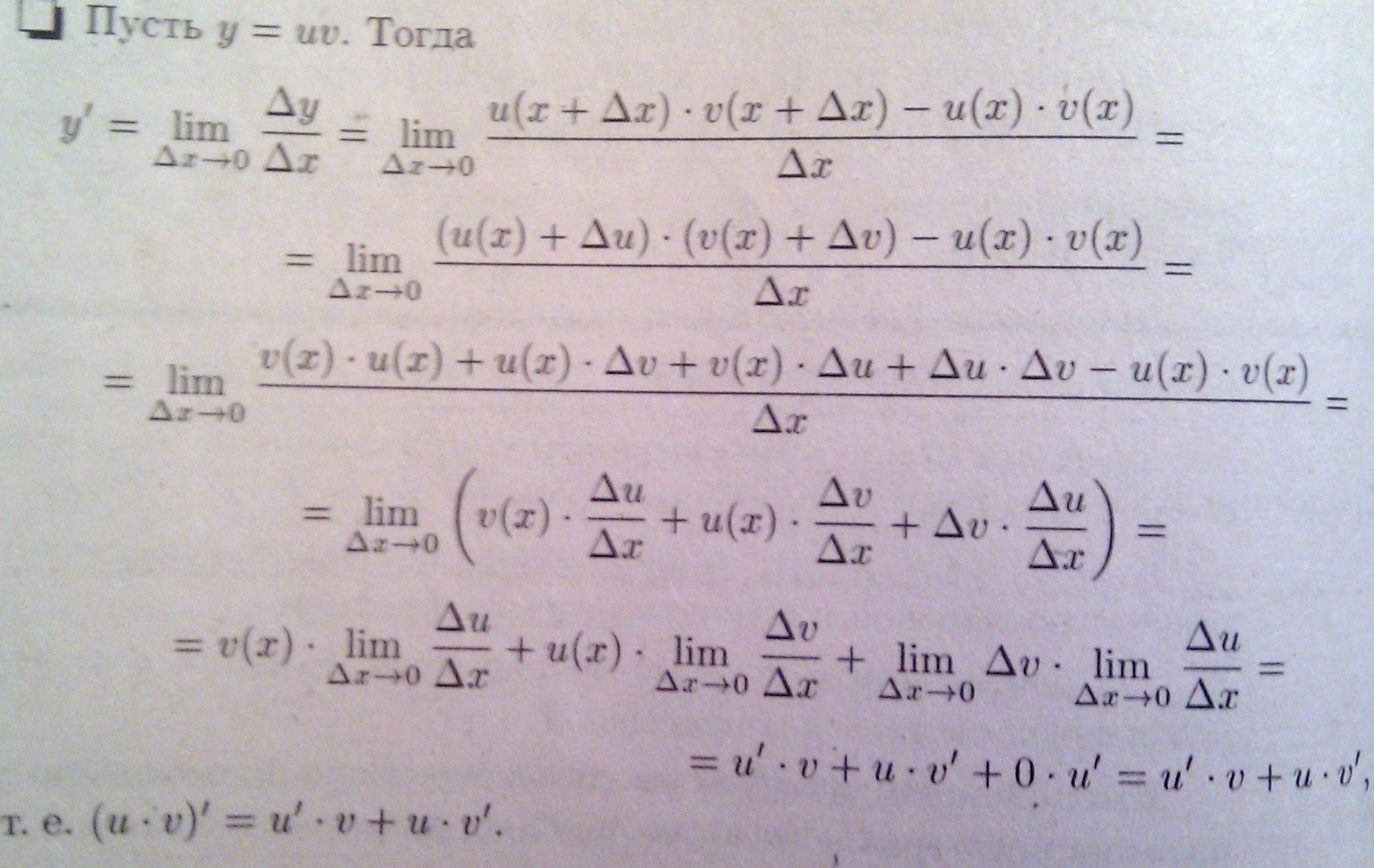
3) Производная частного 2х ф-ций u(x)/v(x), если v(x)не=0 является дробью: числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель: есть квадрат прежнего знаменателя. (u/v)`= (u`*v-u*v`)/v2
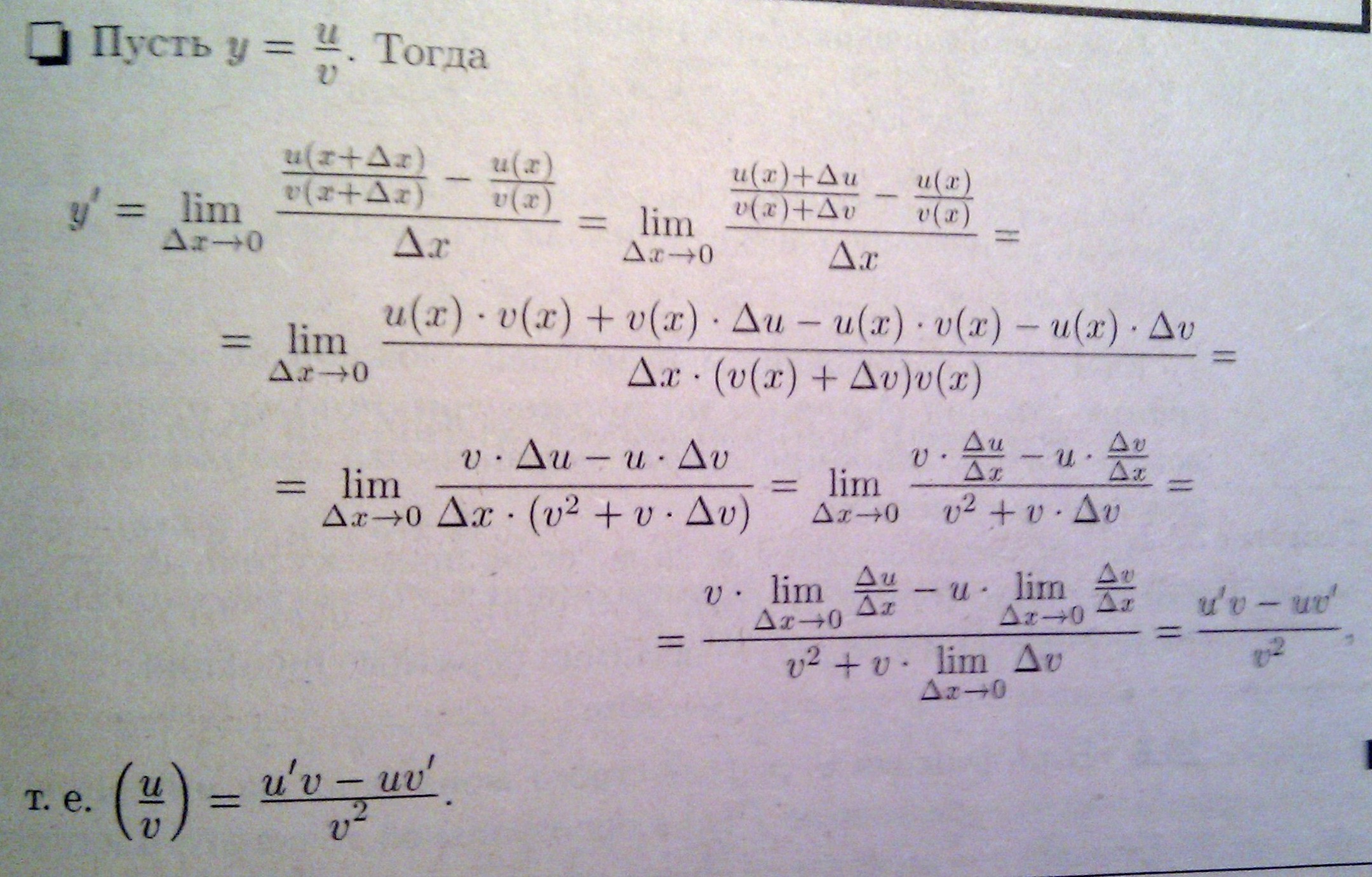
4) Некоторый множитель мб вынесен за знак производной (c*f(x))`=c*f`(x), c=const
Применем 2 св-во: c*(f(x))`=c`*f(x)+c*f`(x)=c*f`(x), тк c`=0
30. Таблица производных
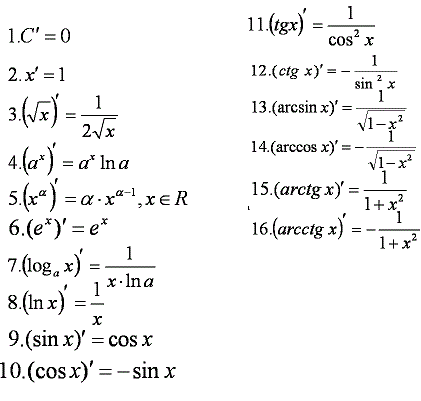
33. Определение ф-ции дифф. В точке./необх. И достаточность
Опр. y=f(x) называется дифф. в (.) х0, если ее Dу можно представить Dу=А*Dх+а(Dх)*Dх, где А – некоторое число, независящее от Dх, а а(Dх) – ф-ция аргумента Dх являющаяся бмф при Dх->0.
(т) Для того, чтобы ф-ция y=f(x) была дифференцируемой в (.) х0 необходимо и достаточно, чтобы она имела в этой точке конечную производную. Док-во:
Необходимость: Если y=f(x) – дифференцируема, то она имеет конечную производную. Тк y=f(x) диффер, то ее приращение Dy=А*Dх+а(Dх)*Dх. Разделим обе части на Dх => Dу/Dx=A+a(Dx)
y`=limDy/Dx(при Dх->0)=lim(A+a(Dx))(при Dх->0)=A
Достаточность: Пусть у ф-ции у=f(x) сущ-ет конечная производная. Докажем, что она дифференц. y`=limDy/Dx(при Dх->0)=А ; limDy/Dx(при Dх->0) -А=0 ; limDy/Dx(при Dx->0) – limA(при Dх->0)=0 ; lim(Dy/Dx – A)(при Dх->0)=0 => ф-ция Dу/Dх – А – бмф(при Dх->0). Обозначим её через а(Dх)= Dу/Dх – А
а(Dх)*Dх=Dу-А*Dх ; Dу=а(Dх)*Dх+А*Dх => у=f(x) – дифференц. ф-ция
34. Понятие дифференциала и его геом. Смысл
Пусть ф-ция y=f(x) дифференц. в (.) х0. Тогда ее Dy можно записать в виде 2х слагаемых: Dу=А*Dх+а(Dх)*Dх, где а(Dх) – бмф при Dx->0. Рассмотрим слагаемое A*Dx – бмф одного роядка с Dх, т к lim(A*Dx)/Dx(при Dх->0)=A≠0
Рассмотрим 2 слаг. А(Dх)*Dх – явл. бмф более высокго порядка, чем Dх, т к lim a(Dx)*Dx(при Dх->0) = 0, таким образов 1 слаг. при А≠0 – главная часть приращения y=f(x)
Опред. Диффер. ф-ции y=f(x) в (.) х0 называется главная линейная относительно Dх часть приращения ф-ции в этой точке: dy=A*Dx
Если А=0, то и в этом случае полагаем, что А*Dх – гл. часть приращения. В этом случае dy=0, учитывая, что А=f`(x0) получаем, что dy=f`(x0)*Dx. Если f(x)=x, то dy=dx=lim((x-Dx-x)/Dx)(при Dх->0)*Dх=Dх (тк lim((x-Dx-x)/Dx)(при Dх->0) и есть f`(x)). Таким образом dx=Dx
Геом. смысл. дифф.Рассмотрим график производной ф-ции f(x) (рис). Тогда проведем касательную к графику в (.) М. Рассмотрим DАВС – прямоуг. tga=AB/AM ; tga=k=f`(x0) ; AM=Dx ; АВ=f`(x0)*Dx=dy
Дифференц. ф-ции y=f(x) в (.) х0 равен приращению ординат касательной к графику ф-циив этой точке, тогда x0 получит Dх