1. Множества

М. – любая совокупность к-л предметов, эти предметы – элементы множества. Множества – конечные(содержащие определённое число элементов)/бесконечные (беск. число элемен.).

Счётное мн. – мн., элем. которого можно поставить во взаимно однозначное соответствие (перенумеровать) с мн. натуральных чисел (N) N – тоже счетн. мн. Счётным является любое бесконечное подмн. множ-ва N (fe мн. чётн. чисел – счётное)

Несчётное мн. - такое ∞ мн., которое не является счётным.

Конечные мн. можно задать перечисляя их элементы в {}. Д/беск. мн. такой способ невозможен. Множ. можно задать указывая их св-ва, характеризующие его элем. x={x|x²=4}

Пустое мн. – не содерж. ни одного элемнт.

Подмножество – если все элем. А являются элемент. мн. B (АсВ)

Универсальное мн. – содержащее все мыслимые объекты, оно единственно.

2. Операции над мн.

Объединением мн-тв А и B называют мн., элементами которого являются все элементы множ. А и все элем. множ. В, одинаковые элемент. включаются в объединение только 1 раз. (АUВ)

Пересечением мн-тв А и В – мн., элементы кот. явл. одновременно элемент. А и В (А^В)

Разность А и В – мн., элем. котор. явл. все элементы мн. А, не входящие в мн. В

Дополнением множества А до универс. мн. – мн., состоящее из элементов, не принадлежащих А.

; ; ; ;

3. Числ. Прям./промеж./ ɛ-окр./модуль

Числ. ось – прямая линия, на которой выбраны: некоторая точка O - начало отсчёта (0);

положительное направление, указанное стрелкой; масштаб для измерения длин (единичный отрезок). Числовые промежутки: Интервал на числ. оси – мн. действ. чисел Х, таких что {x принадл. R| a<x<b} или (а; b). Полуинтервалом – мн. действ. чисел X, тч {x принадл. R| a ≤ x < b} или {x принадл. R | a<x≤b} [а;b) или (а; b] Промежутком на числ. оси – мн. таких действ. чисел {x принадл. R| a≤x≤b} или [a;b]

Модуль ; ; ; ; ; ;

;

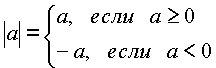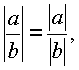Эпсиолн (ɛ) окрестности V_ɛ(x₀) – мн. таких действ. чисел, которое удовлетворяет условию

{x принадл. R| |x-x₀| < ɛ } или (х₀ - ɛ; х₀ + ɛ), x₀ – центр окрестности; ɛ - радиус.

7. Бб посл. И бм посл.

Пос-ть {x_n} – бб, если д/любого «+» числа М сущ-ет такой номер n, такой что д/всех элементов посл-ти с номером n>N выполняется |x_n|>M

Посл-ть {x_n} – бм, если д/любого «+» числа ɛ, сущ-ет такой номер N, такой что д/всех членов посл-ти больше этого N выполняется |x_n |< ɛ ( + На языке эпсилон-дельта)

Установим связь между бб и бм: (Т): Если посл-ть {x_n } – ббп и все её члены отличны от нуля, то {1/x_n } – бмп и обратно, если …

Док-во: Пусть {x_n} – ббп. Возьмём ɛ>0, пусть число М=1/ɛ. По опред. ббп д/этого числа М сущ-ет такой номер N, такой что д/всех элементов с номерами n>N выполняется неравенство |x_n | > M; 1/|х_n| < 1/M; |1/x_n| < 1/M, те (1/x_n)< ɛ

Это означает согласно определения бмп, что послед. {1/x_n} – бмп. Обратное утвердение доказывается аналогично {x_n} – ббп  {1/х_n} – бмп.

8. Опр. фун-ции, св-ва, сложная и обр. фун-ция

Если каждому элементу х их мн. Х по некоторому правилу соотв. единственный элемент у из мн-ва У, говорят, что задана ф-ция y=f(x). Таким образом ф-ция определена, если заданы мн. Х(обл. опр.), мн. У (обл. знач.), правила сопоставления х и у.

Способы задания: 1Табличный – ф-ция задаётся таблицей ряда значений аргумента и соотв. им знач. ф-ций; 2Графический – задаётся гр. ф-ции, значение ф-ции у соответств. значениям х находятся непосредственно из графика; 3Аналитический – задаётся в виде 1 или нескольких ф-ций (уравнений).

Св-ва: 1Монотонность: Пусть у=f(x) на D, пусть мн. D₁ c D.

а) для люб. х₁, х₂ принадл. D₁ выполняется условие таких что x₁<x₂ и f(x₁)< f(x₂), то ф-ция строго возрастающая на D₁ (Большему значению аргумента соотв. большее знач. ф-ции)

б) д/люб. х₁, х₂ принадл. D₁ ; х₁<x₂ ; f(x₁) ≤ f(x₂) , то ф-ция возрастающая на D₁

в) д/люб. х₁, x₂ принадл. D₁ ; x₁<x₂ ; f(x₁) > f(x₂), то ф-ция строго убывающая … (Юольшему значению аргумента соотв. меньшее знач. ф-ции)

г) д/люб. x₁, x₂ //-// ; f(x₁) ≥ f(x₂) убывающая на D₁

2Чётность: ф-ция у=f(x), определённая на мн. D – чётная, если д/люб. x принадл. D –x принадл. D и f(x)=f(-x) ; ф-ция нечётная, если д/люб. x принадл. D –x принадл. D и f(-x)= -f(x)

3Ограниченность: ф-ция ограниченная, если существует такое «+» число M, что |f(x)| ≤ M для всех значений x .

Сложная ф-ция. y=f(u) на D ; u=φ(x) опр. на D, причем u(x) принадл. D => на D опред. ф-ция y=f(φ(x)) – сложная ф-ция(суперпозиция ф-ции от ф-ции); u=φ(x) – промежуточный аргумент сложной ф-ции.

Обратная ф-ция. y=f(x) с обл. опред. D и множ знач. E. Если каждому у принадл. Е соотв. единств. x принадл. E, то определена ф-ция х=φ(у) – обратная д/y=f(x) => они взаимообратны.

x (x принадл. D)= φ(у)=f^-1(у), чтобы найти обр. ф-цию => решить относительно х ур-ние у=f(x). Из опр. об. ф-ции => ф-ция y=f(x) имеет обратную тогда и только тогда, когда ф-ция f(x) задаёт взаимно однозначное соотв. между мн-вами D и E => любая строгомонотонная ф-ция имеет обратную (если ф-ция ↑ то и обр. ↑, если ↓ то и обр. ↓)