1.3 Построение двумерных графиков в ортогональной системе координат для различных типов данных

Выше рассмотрено построение графиков, когда выражение функций записано непосредственно в области построения графиков. Фактически это означает, что процесс построения графиков совмещён с вычислением ординат функций. Однако в Mathcad'е это не единственный способ. Некоторые другие из них описаны ниже.

1.3.1. Построение графиков в тексте вычислительной программы

Как правило, в инженерных расчётах построение графиков не является самоцелью, а является средством отображения результатов порой достаточно сложных расчётов. Для вывода результатов в графическом виде нужно:

• в математической области присвоить выражение выводимой функции (рис. 20 а);

• установить курсор ниже математической области;

• щелчком мыши на панели Graph на экран вызвать область построения графика;

• в области построения графика в placeholder 6 на рис.2 напечатать имя функции;

• щёлкнуть мышью вне области построения графика или нажать клавишу ввода (Enter).

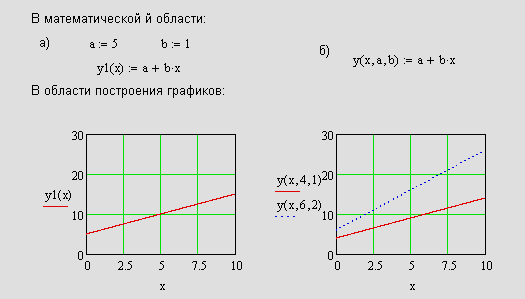
а б

Рис.19. Графики прямой с разными параметрами

Если требуется построить график функции, зависящей от параметров, то параметры в математической области должны быть записаны в скобках после имени функции через запятую.

Например, уравнение прямой в математической области должно быть записано в виде: y(x,a,b):=a+b*x. В области построения графиков имя функции должно записываться с конкретным значением параметров a и b, например, в виде: y(x,a,b):= =(x,4,1).

Когда требуется построить несколько графиков для разных параметров, имя функции записывается в placeholder 6 на рис.2 через запятую, например, как показано на рис.19,б.

1.3.2. Построение графиков по табличным данным

В практических расчётах часто возникает необходимость в графическом представлении табличных числовых данных, полученных из эксперимента или импортированных из каких–либо других объектов, например из Exel. Для построения графиков в этом случае необходимо:

• представить табличные данные в виде матрицы-столбца значений аргумента xdata и соответствующему ему матрицы-столбца значений функции y data (созданию матриц посвящена лабораторная работы № 3);

• войти в область построения графиков описанным выше способом;

• напечатать в имя аргумента данных x data (позиция 2 на рис.2);

• напечатать в placeholder функции (позиция 6 на рис.2) имя данных уdata;

• ввести данные щелчком мыши или клавишей Enter.

По умолчанию график будет построен в виде линии (рис.20, а)).

При необходимости изменить формат вывода графика нужно перейти в окно Traces. Если в меню этого окна выбрать Symвol ромб, а затем в меню Type – stem(ножка), график приобретает вид, представленный на рис.20, б.

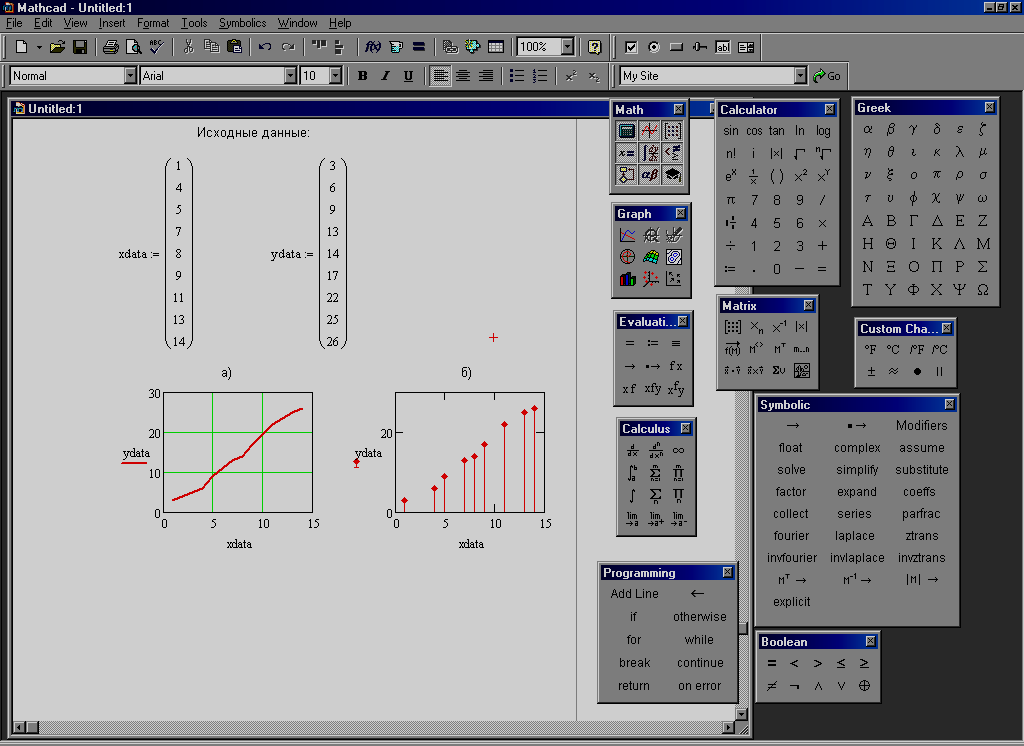
Рис. 20.

3. Построение гистограмм

Построение гистограмм не отличается принципиально от изложенного выше алгоритма построения графиков по данным, заданных таблично. Предположим, что требуется построить гистограмму, исходные данные для построения которой заданы в виде матрицы размерности 2*n, где n – число строк (рис.21).

Для построения гистограммы матрицу данных нужно преобразовать, выделив отдельно матрицу-столбец абсцисс в таблицу , а матрицу-столбец ординат в таблицу . Для этого следует:

• переместить курсор в нужное место рабочего листа;

• щёлкнуть на панели Matrix опцию 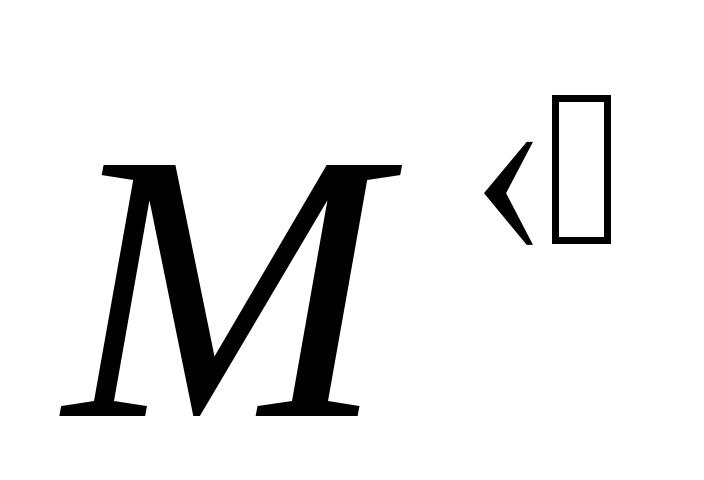, чтобы вызвать шаблон ;

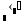• заполнить шаблон для матрицы-столбца аргумента и напечатать знак «=», после чего матрица-столбец отобразится в виде таблицы (на рис.21 в центре);

• повторить те же действия для получения матрицы-столбца ординат;

• войти в область построения графика;

• выделить курсором placeholder обозначения оси и щелчком мыши по опции 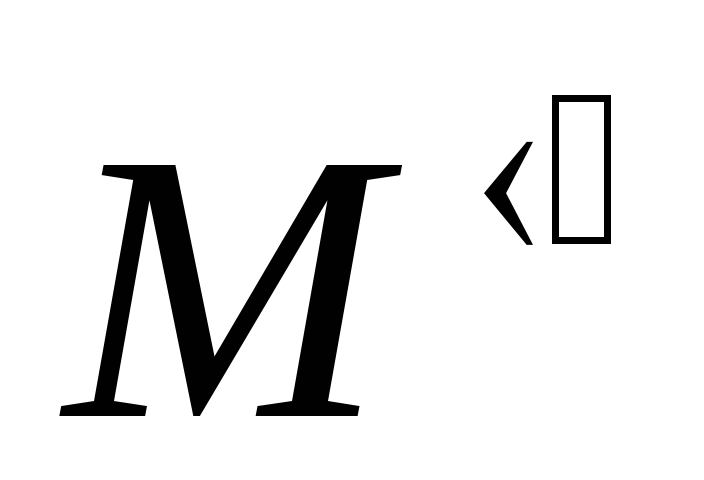вставить на его место шаблон и заполнить его, чтобы он принял вид ;

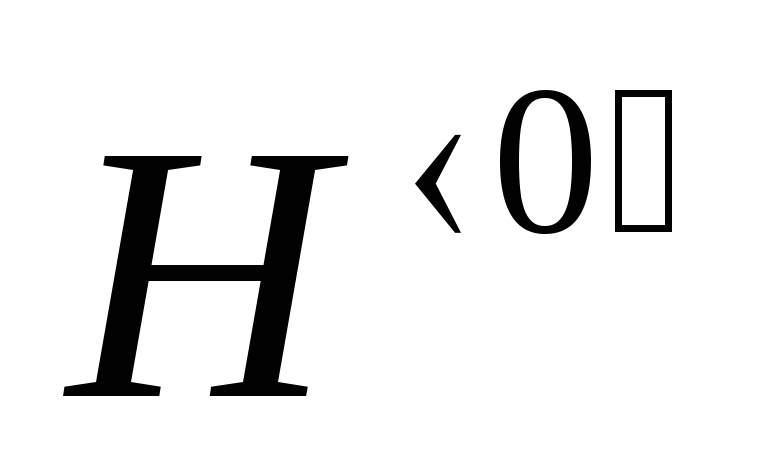• повторить те же действия для оси ординат, чтобы её обозначение приняло вид ;

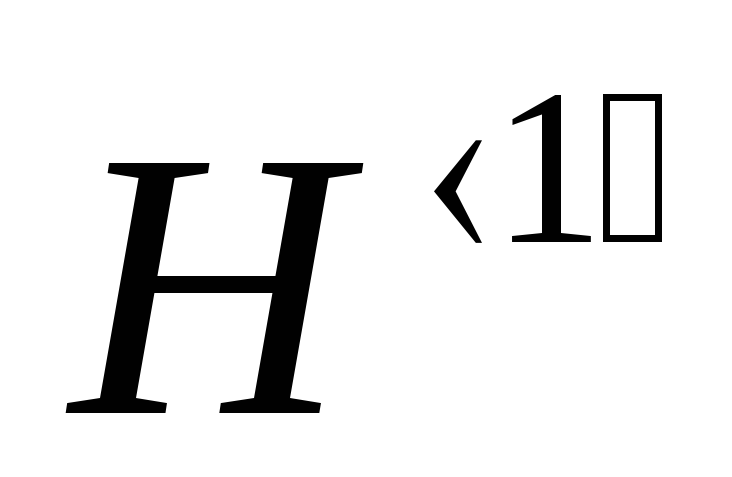• щёлкнуть мышью вне области графика.

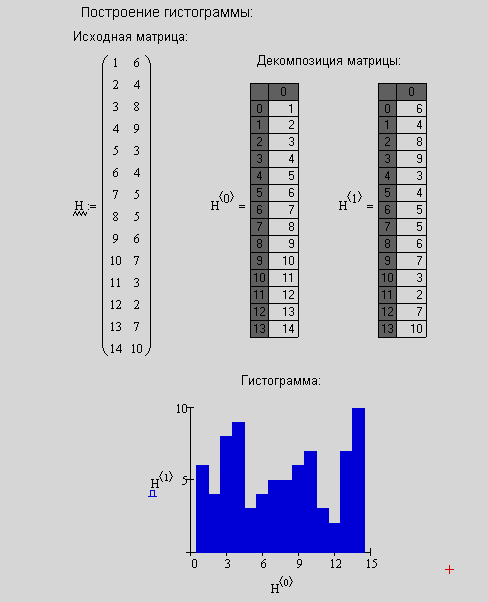
Рис. 21. Построение гистограммы

В результате этих действий график изобразится в виде ломаной, показанной на рис.22.

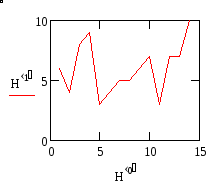
Рис. 22. График исходной матрицы H

Для отображения этого графика в виде гистограммы, необходимо:

• щелчком мыши по графику вызвать окно форматирования Formatting Currently Selected X-Y Plot;

• перейти в окно Traces;

• войти в меню Type и выбрать опцию Solidbar;

• нажать клавишу «применить», а затем «ОК», после чего график примет вид гистограммы.

Дальнейшие действия по форматированию изображения не отличаются от описанной процедуры форматирования обычных графиков непрерывной функции.