
- •«Математическое моделирование систем и процессов»
- •Лабораторная работа № 1
- •1. Интерфейс программного пакета MathСad
- •2. Ввод и вывод информации
- •3. Применение встроенных функций MathСad' а
- •4. Формат представления численного результата
- •5. Вычисление производных и интегралов
- •5.1. Вычисление производных
- •5.2. Вычисление интегралов заданных функций
- •6. Редактирование рабочего листа
- •6.1. Копирование, удаление и перемещение объектов рабочего листа
- •6.2. Ввод текста
- •7. Содержание лабораторной работы.
- •Варианты задания
- •8. Отчет по лабораторной работе
- •Лабораторная работа №2
- •1. Построение и редактирование двумерных графиков в декартовой системе координат.
- •1.1. Построение графиков
- •1.2. Форматирование двумерных графиков в декартовых координатах
- •1.3 Построение двумерных графиков в ортогональной системе координат для различных типов данных
- •1.3.1. Построение графиков в тексте вычислительной программы
- •1.3.2. Построение графиков по табличным данным
- •Построение гистограмм
- •1.3.4. Построение графиков дискретных функций, заданных системой неравенств
- •3. Содержание работы.
- •Лабораторная работа № 3
- •1. Системы линейных уравнений
- •1.1. Запись векторов и матриц в MathCad
- •1.2. Решение систем линейных алгебраических уравнений методом обратной матрицы
- •1.3. Решение системы линейных алгебраических уравнений встроенной функцией lsolve
- •1.4. Решение системы линейных алгебраических уравнений блоком Given…Find
- •2. Системы нелинейных алгебраических уравнений
- •2.1. Решение с помощью вычислительного блока Given…Find
- •2.2. Решение системы нелинейных алгебраических уравнений вычислительным блоком Given…Minerr.
- •3.3. Решение системы алгебраических уравнений в символьной форме
- •4. Размерные величины в решающем блоке
- •Содержание и порядок выполнения работы.
- •Варианты для самостоятельной работы.
- •Цель лабораторной работы № 4
- •1. Решение оду с помощью решающего блока Given …Odesolve
- •2. Решение оду первого порядка
- •2.3. Решение оду n-го порядка с одной неизвестной функцией
- •2. Решение систем оду первого порядка
- •2. Решение системы оду методом Рунге-Кутта
- •2.1. Решение системы оду методом Рунге-Кутта с фиксированным шагом интегрирования (функция rkfixed)
- •Решение системы оду методом Рунге-Кутта с автоматическим выбором шага интегрирования (Rkadapt)
- •3. Решение системы оду методом Булирша – Штера (функция Bulstoer)
- •5. Решение системы оду методом Розенброка (функция Radau)
- •6. Содержание лабораторной работы.
- •Библиографический список
- •«Математическое моделирование систем и процессов»
- •Самара 2008
- •«Быстрые клавиши» в MatCad.
1.2. Решение систем линейных алгебраических уравнений методом обратной матрицы
В матричной форме система линейных уравнений имеет вид:
M * X = v, (1)
где М - квадратная невырожденная матрица коэффициентов размерности n x n;
X - матрица-столбец неизвестных – вектор x ;
v - матрица-столбец правой части системы – вектор v;
n - порядок системы уравнений.
Решение такой системы алгебраических уравнений методом обращения матрицы коэффициентов, как известно, записывается в виде:
Х = M-1 v, (2)
где М-1 - квадратная невырожденная матрица, обратная матрице коэффициентов, определяемая из условия М*М-1 =Е;
Е - единичная матрица (диагональные элементы равны единице, остальные – нулю).
Для решения системы n-линейных алгебраических уравнений с невырожденной матрицей М, соответствующей, например, уравнениям (1), с помощью встроенной функции MathCad данным методом необходимо:
-
создать на рабочем листе квадратную матрицу коэффициентов заданных уравнений;
-
создать матрицу-столбец (вектор v) правой части системы уравнений (4.1), выполнив те же действия, что и выше, но для матрицы с числом строк (Rows) равным n и числом столбцов (Columns) равным единице соответственно;
-
напечатать решение в виде: « Х [Shift]: M^-1[пробел] *v»;
-
напечатать Х =(равно) для просмотра числового значения полученного решения.
Внимание:
Для оценки
свойств матрицы М целесообразно вычислить
её определитель, который для неособенной
матрицы должен быть отличен от нуля,
т.е. Det![]() 0.
Для вычисления определителя следует
переместить курсор (красное перекрестие)
ниже матрицы и щёлкнуть мышью по кнопке
Determinant (определитель) на панели Matrix,
вставить
имя матрицы в шаблон (в примере символ
М), переместить курсор (синий уголок)
нажатием клавиши «пробел» и напечатать
знак = (равно) для отображения численного
значения определителя.
0.
Для вычисления определителя следует
переместить курсор (красное перекрестие)
ниже матрицы и щёлкнуть мышью по кнопке
Determinant (определитель) на панели Matrix,
вставить
имя матрицы в шаблон (в примере символ
М), переместить курсор (синий уголок)
нажатием клавиши «пробел» и напечатать
знак = (равно) для отображения численного
значения определителя.
1.3. Решение системы линейных алгебраических уравнений встроенной функцией lsolve
Для решения системы линейных алгебраических уравнений с помощью встроенной функции lsolve необходимо:
-
создать квадратную матрицу коэффициентов уравнений, например, с именем М, и вектор (v) правых частей системы уравнений описанным выше способом;
-
напечатать X[Shift][:] lsolve(M,v), а затем X=(равно) для отображения результата решения.
На рисунке 5 приведен пример решения такой системы. Как и в предыдущем случае, результат решения будет выведен в виде вектора-столбца Х. Если правая часть системы уравнений записана в виде строки, например, при копировании данных из другого приложения, то она должна быть преобразована транспонированием в матрицу-столбец. Это преобразование может быть записано в виде отдельной инструкции: v := V1T , или непосредственно в операторе: X:=lsolve(M,V1T).
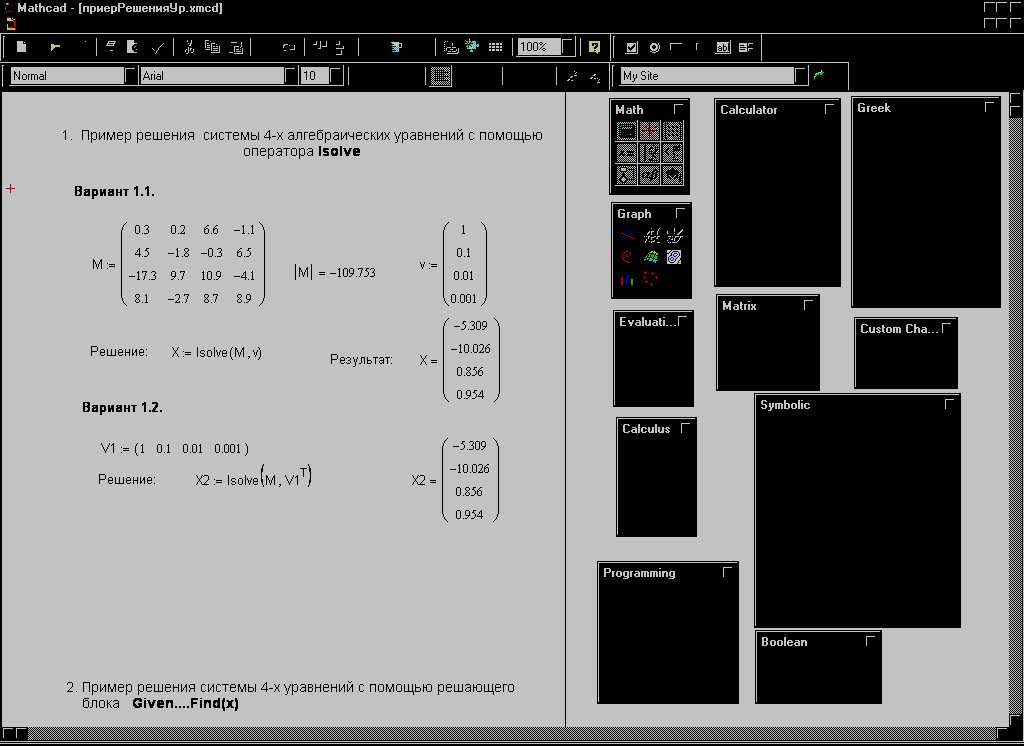
Рис 5. Решение системы алгебраических уравнений
встроенной функцией lsolve
Отметим, что функция lsolve может быть вызвана из списка встроенных функций MathCad . Для этого нужно:
-
напечатать x[Shift]:
-
на панели главного меню щёлкнуть значок f(x);
-
в открывшемся окне Insert Function (вставить функцию) в разделе Categjry Function (категория функции) выделить команду Solving(решатель);
-
вставить нажатием клавиши « insert (вставить) » после знака присвоения (:=) шаблон функции lsolve с двумя placeholder и заполнить его, напечатав имя матрицы коэффициентов и имя вектора правой части системы уравнений;
-
для просмотра решения напечатать Х=(равно).
