3. Применение встроенных функций MathСad' а

В библиотеке программного пакета MathCad содержится около трёхсот специальных функций, которые могут выполняться самостоятельно или в составе вычисляемого математического выражения.

Для того, чтобы внести в рабочий лист встроенную функцию MathCad нужно щелчком левой кнопки мыши по значку f(x) главного меню открыть окно Insert Function (вставить функцию). В списке окна Category Function (категория функции) выбрать нужный раздел, используя полосу прокрутки, а затем в списке второго окна - Function Name (имя функции), выбрать оператор искомой функции. После нажатия клавиш Insert (вставить) и ОК в месте расположения курсора будет вставлена собственно функция или её шаблон.

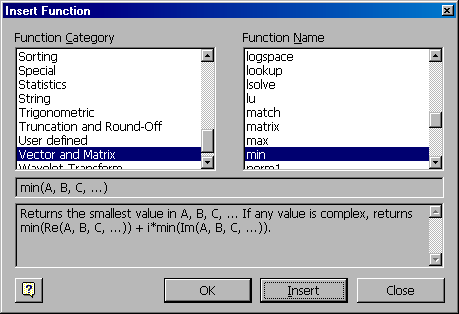
Рис.9. Пример вызова функции min (A,B,C,…)

На рис. 9. приведен пример вызова функции min (A,B,C,…) раздела Vektor and Matrix(векторы и матрицы). Функция возвращает минимальный элемент в матрицах A,B,C,…(для комплексных элементов матрицы – комплексное число с min действительной и min мнимой частей).

Отметим, что шаблоны некоторых наиболее часто употребляемых функций, например тригонометрических и других, могут быть введены простым щелчком левой клавиши мыши соответствующего значка на панелях Calculator, Matrix, Symbolic и др.

На рис. 10 в качестве примера применения встроенных функций MathСad' а приведены примеры действий с комплексными числами: Re(z) - выделение вещественной и Im(z) – мнимой частей, arg(z) - вычисление аргумента.

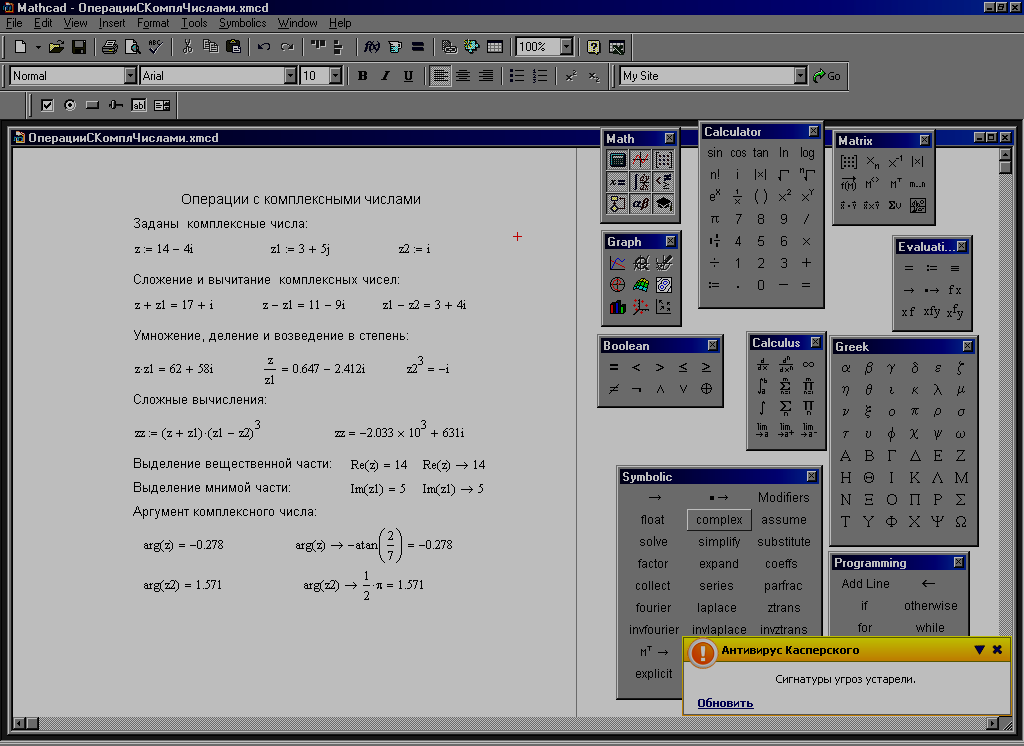
Рис.10. Пример применения встроенных функций Mathcad' а

4. Формат представления численного результата

В Mathcad числа могут быть представлены в одном из пяти форматов, которые приведены на рис.11.

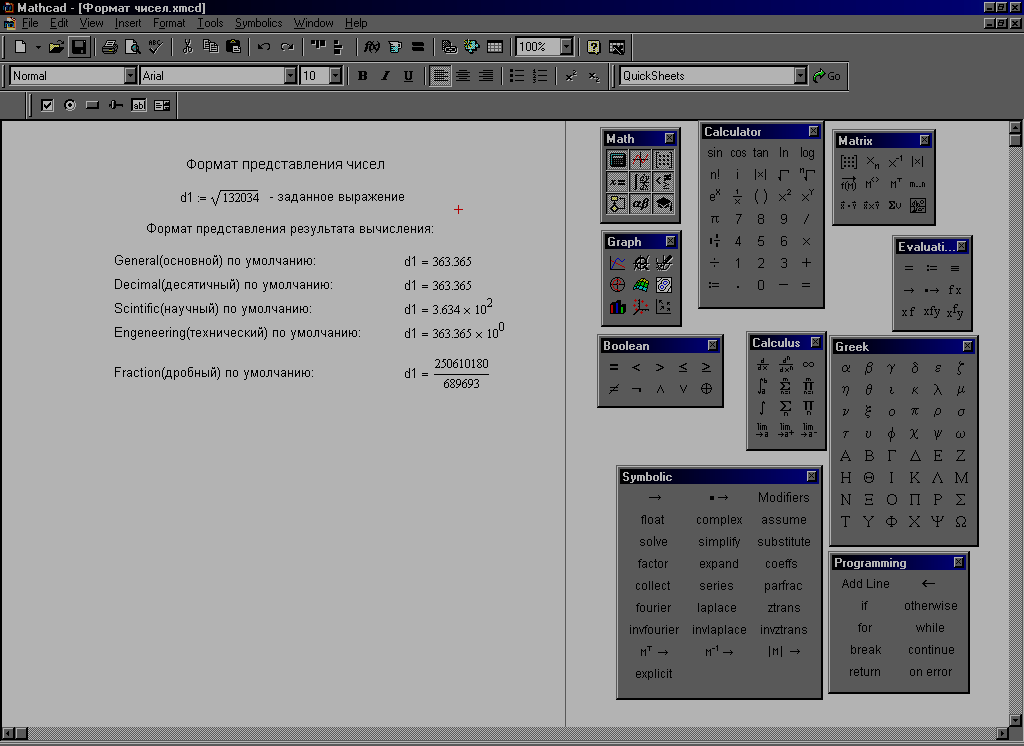
Рис.11. Формат вывода численных результатов по умолчанию(default).

По умолчанию (default) при запуске MathCad устанавливается основной (General) формат, относящийся ко всему рабочему листу. В данном формате число выводится на экран или печать с 3-мя значащими цифрами после десятичной точки. Чтобы перейти к другому формату или изменить в том же формате число значащих цифр, необходимо в выпадающем меню Format (формат) главного меню выбрать вкладку Result (результат) и щелчком левой кнопки мыши открыть окно Result Format (формат результата).

5. Вычисление производных и интегралов

5.1. Вычисление производных

Производные функции одной переменной любого порядка в Mathcad могут вычисляться как в общем (символическом) виде, так и численно, т.е. для заданного значения аргумента функции. При символьных вычислениях производная отображается в аналитическом виде, при численных – в виде числа. Выбор формы представления результата зависит от его использования в дальнейших расчётах и также отличается сравнительно большим разнообразием. Варианты записи и вычисления производной функции одной переменной представлены на рис. 12.

Запись производной в рабочий лист производится заполнением шаблона, который выводится на экран либо с клавиатуры нажатием сочетания клавиш [Shift] /(слеш) для первой производной и [Ctrl]+[Shift] / для производной более высокого порядка, либо щелчком мыши по соответствующему символу на панели вычислений (Calculus).

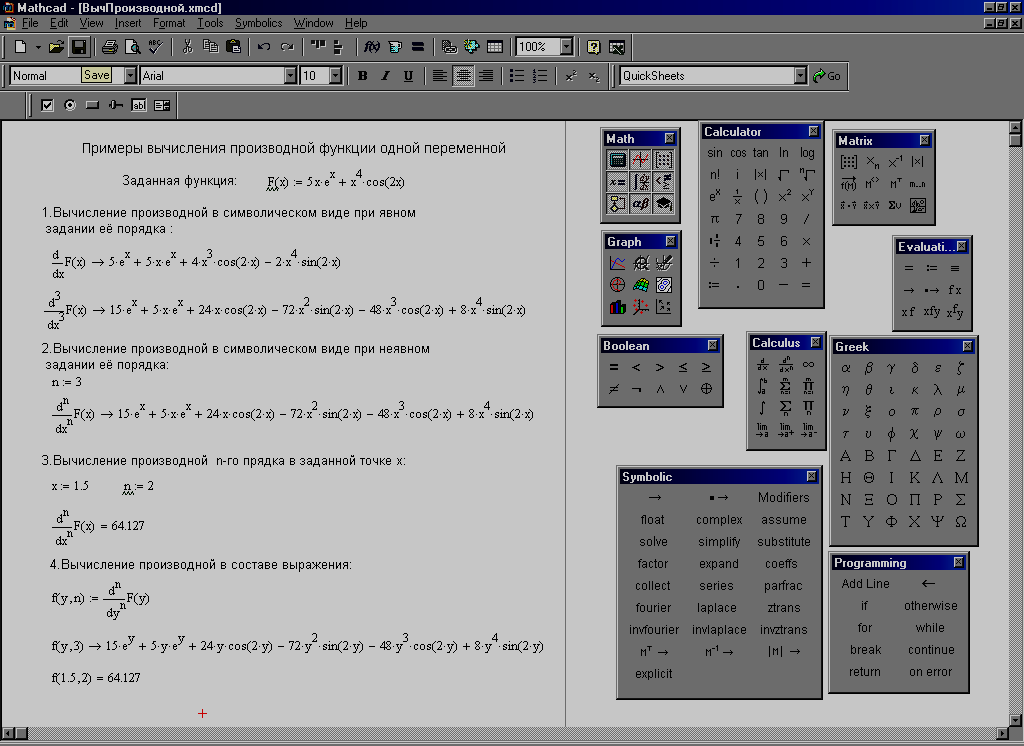
Рис.12. Примеры записи и вычисления производных функции

одной переменной

Если требуется вывести результат в общем виде, то после заполнения шаблона производной записывается символьный знак равенства (правая стрелка на панели (Symbolic).

Порядок производной записывается явно (см. п.1 на рис. 12) или неявно в виде идентификатора переменной (см. п.2 на рис.12), которому присваивается конкретное числовое значение целого типа при обращении к производной в заданном месте вычислительного процесса. Выражение для производной может использоваться и в записи более сложного математического выражения.