Варианты для самостоятельной работы.

Таблица 3

№№	Системы линейных уравнений	№№	Системы нелинейных уравнений
1		1
2		2
3		3
4		4
5		5
6		6
7		7
8		8
9		9
10		10

Цель лабораторной работы № 4

Цель работы: изучение основных методов и приобретение навыков решения систем линейных и нелинейных обыкновенных дифференциальных уравнений средствами системы компьютерной математики MathCad.

Многие задачи математического моделирования сложных электротехнических систем сводятся к решению обыкновенных дифференциальных уравнений (ОДУ) с начальными условиями (задача Коши для ОДУ). В MathCad реализовано несколько классических алгоритмов численного решения ОДУ как записанных в виде одного дифференциального уравнения n-го порядка относительно неизвестной функции одной переменной, так и в виде системы линейных или нелинейных уравнений первого порядка. Кроме того, в MathCad имеются функции решения краевых задач ОДУ, например, функция sbval, реализующая решение краевой задачи «методом прогонки».

1. Решение оду с помощью решающего блока Given …Odesolve

Одним из основных блоков решения обыкновенных дифференциальных уравнений в Mathcad является блок Given…Odesolve. Этот решающий блок используется для решения обыкновенных дифференциальных уравнений с заданными начальными условиями, и применим как для решения линейных и нелинейных уравнений n–го порядка с одной неизвестной функцией, так и для решения систем линейных уравнений первого порядка с n неизвестными.

2. Решение оду первого порядка

В случае уравнения первого порядка задаётся одно начальное условие на левом конце интервала интегрирования, т.е. в виде y(t₀)=y₀. Решение уравнения разыскивается на отрезке времени [t₀,t₁]. На рабочем листе алгоритм решения уравнения записывается следующим образом (рис. 1):

• задаётся имя правой части уравнения, например f(t,y), которому присваивается её выражение;

• печатается оператор Given;

• печатается дифференциальное уравнение в классической форме;

• записывается начальное условие;

• решение записывается в виде: y:= Odesolve(t, t1).

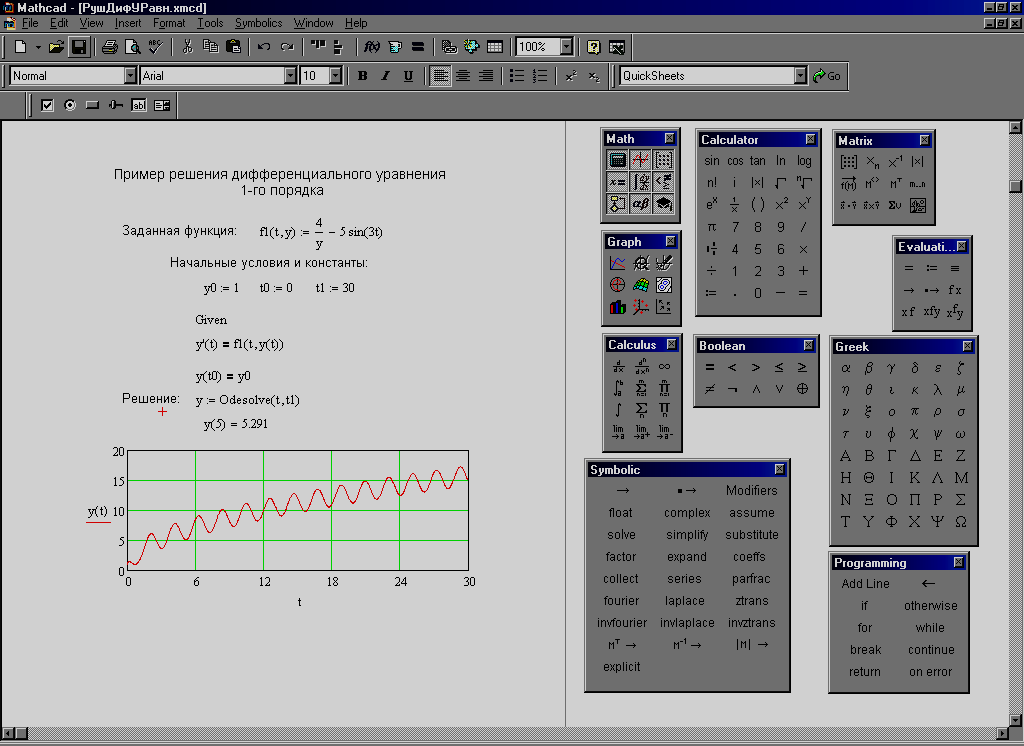
Рис. 1. Пример решения дифференциального уравнения 1-го порядка блоком Given…Odesolve

Примечание. Для ввода главного символа производной «'» необходимо после имени функции напечатать [Ctrl] +F7. Внутри блока Given…Odesolve левая и правая части в записи уравнения и начального условия отделяются только символом эквивалентности(выделенный знак равенства), который вводится комбинацией клавиш [Ctrl] + =(равно) или щелчком мыши на панели Boolean.