1.4. Решение системы линейных алгебраических уравнений блоком Given…Find

Вычислительный блок Given…Find позволяет решать системы до 200 алгебраических уравнений методом последовательных приближений.

В отличие от решения систем уравнений функцией lsolve в блоке Given….Find(X) обязательно должно задаваться начальное приближение для всех неизвестных, входящих в систему уравнений. Начальное приближение присваивается неизвестным уравнений перед оператором Given (задано). Оно может быть введено либо непосредственным присвоением значений неизвестным (рис.6), либо с использованием переменной диапазона. Второй способ (рис.7) предпочтительней при большой размерности системы уравнений, т.к. в этом случае вектор начальных значений может быть создан автоматически.

Для решения системы линейных уравнений с помощью решающего блока Given.Find необходимо:

• присвоить начальное приближение всем неизвестным системы уравнений;

• напечатать оператор Given;

• записать систему линейных уравнений в канонической форме (рис. 6), либо создать матрицу коэффициентов и вектор правых частей системы уравнений (рис. 7);

• напечатать Find (var1, var2,…)=(равно), где var1,var2,.- неизвестные системы уравнений, и просмотреть результат решения.

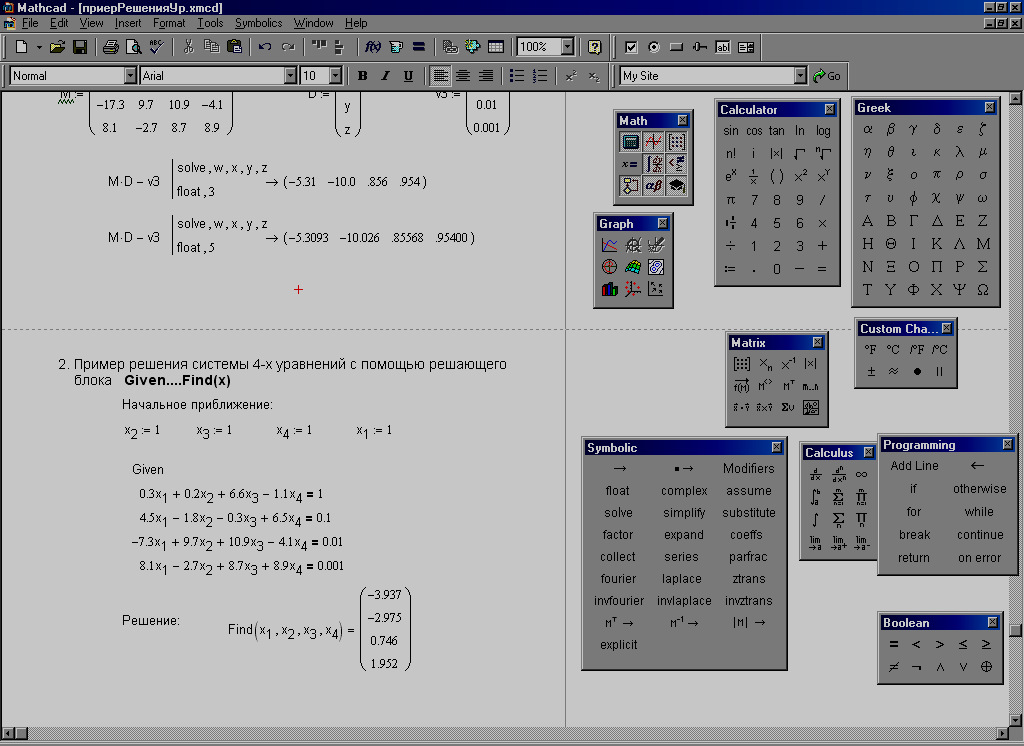
Рис.6. Пример решения системы уравнений

Примечание:

1. В решающем блоке Given…Find уравнения записываются в любой общепринятой форме, в том числе в матричной форме, например, как показано на рис.7.

2. При записи системы уравнений в левая часть уравнений отделяется от правой знаком эквивалентности (выделенное =), который вставляется с панели «Boolean» мышью или может быть напечатан [Ctrl]=(равно) набором на клавиатуре.

3. Внутри блока не должно быть других вычисляемых выражений, кроме уравнений.

4. Функция Find может быть вставлена в рабочий лист из окна Insert Funrtion(вставка функции). Для этого в окне Category Function нужно выделить опцию Solving, а затем в окне Funrtion Name(имя функции) выделить функцию Find. После нажатия кнопки Insert(вставить) на месте курсора отобразится шаблон этой функции.

5. В отличие от функции lsolve в блоке Given…Find должно указываться в обязательном порядке начальное приближение для всех неизвестных.

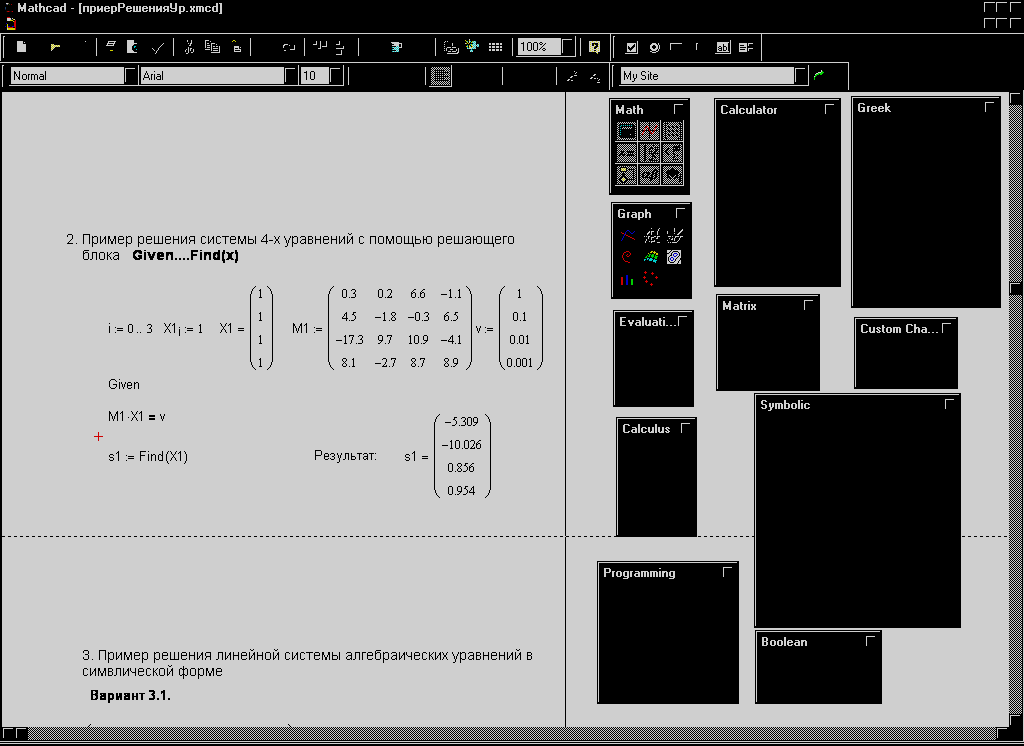
Рис. 7.Пример решения системы уравнений.

2. Системы нелинейных алгебраических уравнений

2.1. Решение с помощью вычислительного блока Given…Find

Наиболее распространённым методом решения нелинейных алгебраических уравнений в MathCad является решение с помощью вычислительного блока Given…Find. Данный вычислительный блок реализует решение методом последовательных приближений, поэтому, как и в случае линейных уравнений, необходимо задавать начальное приближение для всех неизвестных системы уравнений. Последовательность создания рабочего листа следующая:

• присвоить начальное приближение – некоторое численное значение, неизвестным уравнений, например, напечатать: х₁:=а₁ х₂:= а₂ х_n:=а_n, где x_i (i=1,…,n) - имена неизвестных, a_i (i=1,…,n) – заданные числа, n – число уравнений;

• напечатать оператор Given;

• записать заданные уравнения (напомним, что знак равенства вводится нажатием совокупности клавиш Сtrl+=(равно) или щелчком мыши на панели Boolean);

• напечатать vec := Find(x₁, x₂,…, x_n), где vec - идентификатор матрицы-столбца неизвестных;

• напечатать vec= (равно) для вывода результатов решения уравнений и нажать клавишу ввода (Enter).

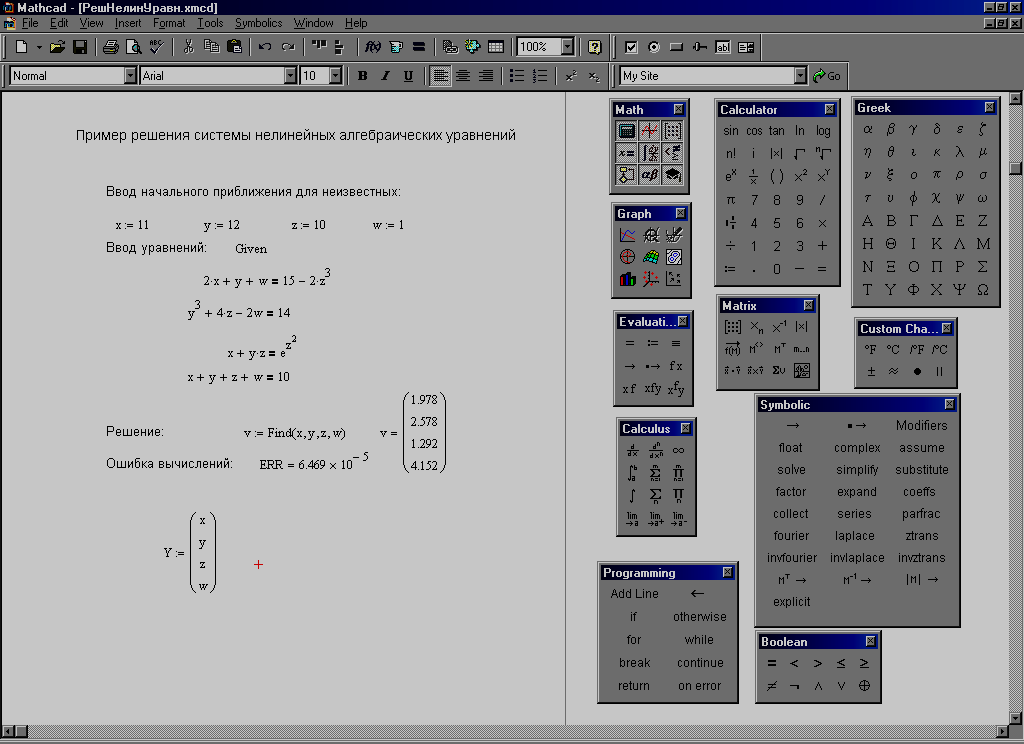
Рис. 8. Пример решения системы нелинейных алгебраических

уравнений блоком Given...Find.